Трехточечиые автогенераторы.

Самовозбуждение простейшего автогенератора.

Исследова­ние процессов в автогенераторах начнем с устройства (рис. 1), называемого автогенератором с трансформатор­ной связью.

Колебательной системой здесь служит LCR-контур, эле­ментом обратной связи — катушка размещенная таким образом, что создаваемый ею магнитный поток частично пронизывает катушку L.

Пусть в устройстве каким-либо образом возбуждены малые колебания. Если и — напряжение на конденсаторе (и соответственно на управляющем электроде электронного при­бора), то по второму закону Кирхгофа можно составить следующее дифференциальное уравнение, описывающее дан­ную систему:

 

(1)

где і — ток в цепи обратной связи. Знак в правой части (1) зависит от того, каким образом (встречно или согласно) включены катушки L и LСB.

Сделаем основное предположение — будем считать управляющее напряжение и столь малым, что электронный прибор вполне точно может быть заменен управляемым источником тока, выходной сигнал которого линейно зависит от управляющего напряжения:

 

(2)

Здесь i₀ – постоянная составляющая тока; S_ДИФ — дифферен­циальная крутизна вольт-амперной характеристики прибора в фиксированной рабочей точке.

Объединив выражения (1) и (2), получаем сле­дующее уравнение системы:

 

(3)

 

где ω₀ = 1/√LC — частота собственных колебаний контура без потерь.

Варьируя коэффициент взаимоиндукции М, можно изменять коэффициент при производной du/dt. Знак и значение этого коэффициента, как известно, определяют характер свободных колебаний в такой динамической системе.

Если в уравнениях (1) и (3) выбраны верхние зна­ки, то за счет обратной связи будет наблюдаться регене­рация. Если величина М достигает критического значения

 

(4)

 

где Q — добротность контура без учета регенерации, то уравнение (14.38) приобретает вид , свой­ственный идеальной колебательной системе без потерь.

При М > М_кр устройство становится неустойчивым. Введя параметр

 

получим дифференциальное уравнение

 

 

решение которого описывает гармонические колебания с экспо­ненциально нарастающей во времени амплитудой:

(5)

(А и В — постоянные, зависящие от начальных условий).

Практически всегда α<<ω₀ и в соответствии с (5) частота заполнения автоколебаний, возникающих в линейном режиме, близка к частоте собственных колебаний контура.

Подчеркнем физический смысл правильного выбора знака в уравнении (3), который обеспечивает неустойчивость начального состояния автогенератора: для самовозбуждения системы необходимо, чтобы любое возмущение колебатель­ного контура приводило к появлению такого сигнала положительной обратной связи, который, складываясь с перво­начальным возмущением, увеличивал бы его. Именно таким образом трактуется понятие положительной обратной связи в теории автоколебательных систем.

 

Трехточечиые автогенераторы.

На практике вместо авто­генераторов с трансформаторной связью чаще используют так называемые автогенераторы-трехточки, в которых напряжение обратной связи снимается с части колебательного контура. На рис. 2, а, б изображены принци­пиальная и эквивалентная схемы индуктивной трехточки.

Наличие резистора R учитывает все виды потерь в системе — неидеальность реактивных элементов, конечное (хотя и достаточно большое) выходное сопротивление электрон­ного прибора, а также влияние внешних цепей (нагрузок).

Найдем условия самовозбуждения индуктивной трехточки, исследуя характеристическое уравнение этой системы с замкну­той обратной связью.

Если U_BX и U_ВЫХ — изображения сигналов на входе и выходе при разомкнутой цепи обратной связи (рис. 2, б), так что известна передаточная функция К(р) = U_ВЫХ/U_BХ то характеристическое уравнение, описывающее замкнутую цепь, как было выяснено, имеет вид:

 

K(p) = 1 (6)

Для того чтобы найти функцию К(р), учтем, что напря­жение U_ab на зажимах контура возникает за счет тока — S_дифU_вх проходящего через последовательно-параллельно соединенные элементы Z₁ Z₂ и Z₃:

 

Поскольку характеристическое уравнение (6) приобретает вид:

(7)

В данном случае

 

 

Подставив эти выражения в (7) и выполнив не­сложные алгебраические преобразования, получим характеристические уравнения замкнутой системы:

 

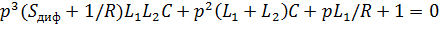(8)

Цепь будет неустойчивой, если определитель Гурвица отрицателен:

 

или

 

Отсюда находим условие самовозбуждения данного автогенератора:

(9)

 

Частота экспоненциально нарастающих собственных ко­лебаний определяется корнями кубического уравнения (8). Аналитическое решение здесь довольно громоздко. Однако из физических соображений ясно, что трехточечный автогенератор самовозбуждается на резонансной частоте . В самом деле, на этой частоте сопротив­ление нагрузки электронного прибора вещественно; комплексная амплитуда напряжения сдви­нута по фазе на 180° относительно .

В контуре наблюдается резонанс токов, элементы L1 и L2 обтекаются одним и тем же контурным током, поэтому .Напряжения и совпадают по фазе, так что при выполнении условия (9) автогенератор действительно самовозбуждается.

Другим вариантом схемы трехточечного автогенератора является так называемая емкостная трехточка, в которой напряжение обратной связи снимается с емкостного делителя, образованного конденсаторами С₁ и С₂. Анализ условий самовозбуждения такой схемы проводится аналогично опи­санному ранее.

RС-автогенераторы гармонических колебаний. На частотах ниже нескольких десятков килогерц применять в качестве колебательных систем автогенераторов резонансные LC-контуры становится затруднительным, главным образом из-за больших массогабаритных размеров индуктивных элементов. Поэтому на этих частотах, как правило, используют RC- автогенераторы, представляющие собой комбинации активных четырехполюсников (усилителей) и пассивных RС-цепей, играющих роль элементов обратной связи.

Пусть К(р) — передаточная функция некоторой разомкну­той цепи и К(р)=1 — характеристическое уравнение, опи­сывающее поведение системы с замкнутой обратной связью. Для того чтобы такая система была неустойчивой и могла генерировать гармонические колебания в стационарном режиме, характеристическое уравнение должно иметь, по крайней мере, одну пару комплексно-сопряженных корней с положительной вещественной частью. Мнимая часть корней будет при этом определять генерируемую частоту.

Получим условие самовозбуждения часто используемого автогенератора с двумя RС-цепями (рис. 3, а).

Основой генератора является идеальный усилитель с ве­щественным и положительным коэффициентом усиления К₀. Выход усилителя соединен с его входом через пассивный RС-четырехполюсник, передаточная функция которого по напряжению в соответствии с рис. 3, б имеет вид

 

(10)

 

Здесь введены следующие обозначения:

Характеристическое уравнение авто­генератора K₀β₁(p)=1, очевидно, можно записать так:

(11)

 

Описываемая система становится неустойчивой при таком выборе параметров, когда коэффициент при первой степени ру проходя через нуль, меняет знак. Для самовозбуждения автогенератора необходимо, чтобы выполнялось неравенство

 

 

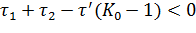
Отсюда получаем условие, налагаемое на коэффициент усиления активного звена:

(12)

 

В частности, если обе КС-цепи идентичны, то системасамовозбуждается, когда К₀ > 3.

Мнимая часть корней уравнения (11) зависит не только от параметров R₁ R₂ C₁ C₂ но и от коэффициента усиления К₀. Для оценки генерируемой частоты будем прибли­женно считать, что автогенератор работает на границе самовозбуждения и поэтому коэффициент при первой степени р равен нулю. Тогда из характеристического уравнения находим значение генерируемой частоты:

(13)

 

Отметим в заключение, что RC-автогенератор существен­но уступает LC-автогенераторам с точки зрения качества спектрального состава генерируемых колебаний. Это связано с тем, что в них цепь обратной связи не содержит колебательных контуров и не может в достаточной мере отфильтровать нежелательные высшие гармоники. Удовлетво­рительная форма генерируемых колебаний достигается спе­циальными схемотехническими мерами, например за счет использования дополнительной цепи нелинейной инерционной обратной связи.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: