 |
Уравнения, решаемые домножением на некоторую функцию обеих частей.
|
|
|
|
Иррациональные уравнения
Напомним, что иррациональными называются уравнения, в которых неизвестная величина содержится под знаком корня или в основании степени с рациональным показателем.
Следует хорошо понимать, что:
1. Все корни четной степени, входящие в уравнение, являются арифметическими, т.е. подкоренное выражение определено только для неотрицательных значений, и сам корень принимает только неотрицательные значения;
2. Все корни нечетной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения.
К основным методам решения иррациональных уравнений относятся:
Возведение обеих частей уравнения в одну и ту же степень;
Замена неизвестного;
Домножение обеих частей уравнения на одну и ту же функцию;
Применение свойств функций входящих в уравнение.
Уравнения, решаемые возведением обеих частей уравнения в одну и ту же степень.
При решении иррационального уравнения этим способом можно идти двумя путями:
I путь
1. Найти область определения уравнения
2. Выполнить преобразования, приводящие данное уравнение к равносильному рациональному
3. Найти множество решений уравнения учетом области определения
II путь
1. Выполнить преобразования данного уравнения, приводящие к уравнениям–следствиям
2. Найти корни уравнения–следствия
3. Выполнить проверку и записать ответ
Примеры:
 (1)
(1)
|

Проверка: а) 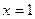

 (верно), значит,
(верно), значит, 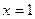 - корень уравнения (1)
- корень уравнения (1)
б) 

 (неверное равенство)
(неверное равенство)
Ответ: 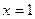
 (2)
(2)
Обратим внимание, что левая часть уравнения представляет собой сумму корней третьей степени.
|
|
|
При возведении в 3-ю степень левой части уравнения удобно воспользоваться формулой  (если надо возвести в третью степень разность корней, то формулой
(если надо возвести в третью степень разность корней, то формулой  )
)
Воспользовавшись формулой, получим
 , откуда
, откуда
 (т.к.
(т.к.  )
)
Разделив почленно это уравнение на 9 и возведя еще раз обе части равенства в 3-ю степень получим
 ,
,
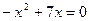 ,
,
откуда  и
и 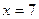
Ответ:  ,
, 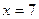
 (3)
(3)
Возведем обе части уравнения (3) в 6-ю степень;
Получим 



 -единственный корень уравнения
-единственный корень уравнения
Ответ:  .
.
Уравнения, решаемые с помощью учета свойств монотонности функции.
Рассмотрим уравнение 
 (1)
(1)
Его область определения составляет луч (-3; +∞)
На этом множестве функция является монотонно возрастающей; значение равное 5, эта функция принимает не более, чем в одной точке. Очевидно, что 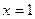 - корень данного уравнения. Его единственность доказана выше.
- корень данного уравнения. Его единственность доказана выше.
Аналогично решается уравнение  . Его область определения есть R, в левой части стоит возрастающая функция, которая обращается в 0 при
. Его область определения есть R, в левой части стоит возрастающая функция, которая обращается в 0 при  .
.
Уравнения, решаемые с помощью исследования области определения.
Рассмотрим уравнения: 
 (1)
(1)
 (2)
(2)
Область определения уравнения (1) не содержит действительных чисел, значит, это уравнение не имеет корней.
Область определения уравнения (2) находится из решения системы 
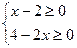
и составляет единственное число  .
.
Проверим, является ли  корнем уравнения (2):
корнем уравнения (2):
 (верно)
(верно)
значит,  - корень уравнения
- корень уравнения
Ответ: 
Уравнения, решаемые с помощью учета свойств ограниченности входящих функций.
 (1)
(1)
Заметим, что для 
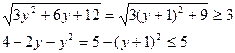
Имеем 
|

Из уравнения (2’) следует, что  , и это значение удовлетворяет уравнению (1’)
, и это значение удовлетворяет уравнению (1’)
Значит  – корень уравнения (5)
– корень уравнения (5)
Ответ: 
Уравнения, решаемые с помощью учета области определения и множества значений входящих в уравнение функции
Решим уравнение: 
Область определения уравнения: 
|
|
|
Если  , то
, то 


Итак, получили, что при  функция
функция  имеет множество значений, не имеющих общих чисел с множеством значений функции
имеет множество значений, не имеющих общих чисел с множеством значений функции 
Вывод: решений нет
Ответ: Ø 
Уравнения, решаемые домножением на некоторую функцию обеих частей.
Рассмотрим уравнение  (1)
(1)
Умножим обе части уравнения на  (при этом область определения данного уравнения не изменится)
(при этом область определения данного уравнения не изменится)
Тогда уравнение (1) будет равносильно системе










Числа 1 и 2 удовлетворяют уравнению (1), значит, являются его корнями.
Ответ: 

|
|
|


