 |
Анализ и решение текстовых задач по методу В. Лебедева
|
|
|
|
В. Лебедев считает, что то, что в школьном курсе математики решение текстовых задач считается одним из самых сложных для восприятия и усвоения учащимися разделов, связано с неразработанностью аналитического аппарата, который бы позволял рассматривать любую текстовую задачу как систему, в независимости от того, является ли она задачей на движение, на работу, на смеси или сплавы, на проценты и т. д[9].
Для того, чтобы рассматривать задачу как систему, нам необходимо определить:
а) элементы задачи;
б) характер взаимосвязей между элементами.
Первый набор элементов, который необходимо определить в задаче как системе – это участники контекста задачи (машина и велосипед, поезда, амфибии и самолеты; рабочие и землеройки, станки и роботы; сплавы цинка и меди, раствор соли и спирта и т. д.)
Действие, производимое участником или с участником, в свою очередь также является системой. Эти действия определяются следующими элементами, которые называются компонентами:
а) скорость V, время t, путь S – движения;
б) производительность T, время t, объем работы V – работы;
в) объем смеси V0, объем вещества в смеси Vв, объемная концентрация вещества в смеси cв, процентная, объемная концентрация вещества в смеси pв% – смеси, сплава, раствора... и т. д.
По условиям задачи происходят различные изменения в значениях компонентов участников или накладываются на них какие-либо ограничения: увеличилась или уменьшилась скорость движения, известно время до встречи; вначале работали вместе, затем увеличилась производительность труда и т. д. Каждое такое изменение характеризует свою систему, состоящую из участников и соответствующих значений компонент. Назовем эти системы состояниями.
|
|
|
Тогда общую систему задачи можно представить в виде:

Структура системы определяется характером взаимосвязи между элементами. Таким образом, для полного раскрытия системы задачи нам необходимо определить взаимосвязи:
1. Между компонентами каждого участника в каждом состоянии. Назовем их вертикальными взаимосвязями.
2. Между компонентами участников в каждом состоянии. Назовем их горизонтальными взаимосвязями или уравнивающими.
3. Между компонентами каждого участника в различных состояниях.
4. Между компонентами участников в различных состояниях.
Необходимость поиска взаимосвязи между компонентами участников в каждом состоянии требует ввести еще один элемент в систему задачи. Назовем его взаимосвязь (или общее).
Теперь таблица системы задачи будет выглядеть следующим образом:

В зависимости от типа задачи таблица, описывающая ее систему, примет соответствующий вид. Например, для задачи на движение:

Движение каждого участника описывает три компоненты. Для того, чтобы найти взаимосвязь между ними, нам необходимо знать значения двух компонент. В традиционном подходе к решению текстовых задач для реализации этого положения вводятся неизвестные величины – x, y и т. д. Мы используем следующий подход. Пусть, например, S21 и S22 (указываем какие-либо из компонент) как будто бы известны и дальше работаем над задачей, исходя из этого.
Например:
Задача 1. Между домами Кролика и Лиса существовала прекрасная дорога в 50 км. Как-то так случилось, что они одновременно пошли друг к другу в гости. Они не пошли, а побежали. Через 5 часов, увлеченные воображаемым приятным времяпрепровождением в гостях, они пробежали мимо друг друга, рассеянно сказав: «Привет». Кролик, задумавшись над тем, неуловимо знакомым только что промелькнувшим мимо него, снизил свою скорость на 1 км/ч. Лис, почуяв что-то из того, что ему грезилось, увеличил скорость на 1 км/ч. Каково же было их разочарование, когда они не застали друг друга дома. У Лиса это разочарование наступило на 2 часа позже, чем у Кролика. С какой скоростью двигался Кролик?
|
|
|
Первым шагом анализа системы задачи мы определяем участников движения. Читаем текст задачи.
1. Сколько участников? – Два (Кролик и Лис).
Вторым шагом определяем состояния: сколько их и какие они.
2. Сколько состояний? – Два (до встречи, после встречи).
Третьим шагом изложим в таблице данные, необходимые для дальнейшего анализа системы задачи.
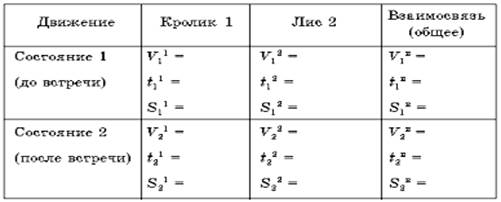
После построения таблицы еще раз читаем текст задачи (четвертый шаг) и заносим в нее данные значения компонентов.
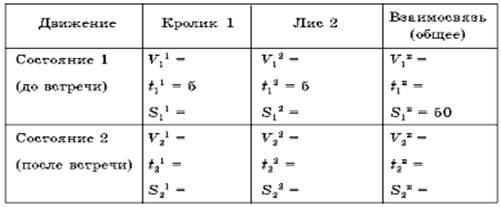
Для того, чтобы проанализировать первое состояние, нам необходимо ввести значения компонент, которые мы как бы знаем. Пусть это будет скорость кролика – V1. Тогда имеем (в скобках цифрами мы проставляем последовательность наших рассуждений):


(4) и (5) получены из анализа взаимосвязи компонентов каждого участника в различных состояниях и условия задачи. (6) и (7) – из анализа взаимосвязи компонентов участников в различных состояниях. (8) и (9) – из анализа взаимосвязи компонентов каждого участника в состоянии 2. (10) – из условия задачи.
На основании (10) имеем уравнение:

решив которое получаем: V1 = 6 км/ч.
Ответ: 6 км/ч.
Можно отметить, что уравнения формируются из взаимосвязей между компонентами участников в состоянии. Поэтому мы и назвали их горизонтальными или уравнивающими.
На учащихся производит большое впечатление, если они понимают, что для анализа системы задачи нет особой разницы в том, какой или какие значения компонентов принять за как бы известные величины. Еще больше их интригует возможность по полностью восстановленной системе задачи составлять свои задачи, переходить от одной задачи к другой.
Таким образом, на рассмотренном примере мы показали, как использовать метод анализа системы задачи, строить уравнения, которые приводят к решению текстовых задач.
Необходимо отметить, что данная методика обучения расширяет возможности учителя по развитию творческого мышления учащихся, позволяет развивать у них целостное и системное понимание математических закономерностей и взаимосвязей.
|
|
|
|
|
|


