Описание случайных погрешностей и понятие доверительного интервала

Погрешности систематические и случайные

Измерение можно назвать правильным тогда, когда

то есть систематические погрешности сведены к минимуму (в идеале – к нулю).

Случайные же погрешности уменьшить нельзя, их можно лишь учесть методами математической статистики.

Систематические погрешности формируются под воздействием постоянных факторов или факторов, меняющихся по определённому закону. Тогда, можем утверждать, что систематическая погрешность остаётся постоянной (или меняется по определённому закону) при многократных измерениях одной и той же случайной величины.

Пример 1:

Здесь систематическая погрешность остаётся постоянной.

к объекту исследования

 

R₀

Пример 2:

Средство измерения

Здесь погрешность меняется по определённому закону.

 

Изменение:

E₀ по экспоненте

 

Систематические погрешности, как уже было сказано, необходимо уменьшить. Как это можно сделать? А, например, вот так:

1) Правильно поставить эксперимент (чтобы никаких помех и шумов при измерениях, чтобы никаких магнитов рядом не было, чтобы никто не отвлекал от снятия результатов и так далее)

Пример:

А в это время в лабораторию, скажем, внесли

постоянный магнит и «испортили» вам результаты.

То, что мы не можем или просто позабыли соблюсти относится к случайным погрешностям.

2) Введение поправок, градуированность графиков

3) Применение специальных методов, например, метода замещения и других…

Случайные погрешности формируются под воздействием факторов, которые могут появиться или исчезнуть с интенсивностью, которую трудно (или невозможно) предсказать. Иными словами, случайные погрешности меняются случайным образом при многократном измерении одной и той же величины.

Пример:

ЦИВ – цифровой измерительный вольтметр

Измерению подлежит напряжение U_R на резисторе.

 

Первая реализация

Время с t₁ ÷ t₂ (например с 9:00 до 10:30)

Проводим измерения и записываем

результаты:

U_R =

99, 99 В

100, 01 В

99, 7 В

…

и так n раз

…

Вторая реализация

Время с t₃ ÷ t₄ (например с 14:30 до 16:00)

Проводим измерения и записываем

результаты:

U_R =

98, 99 В

100, 05 В

101, 7 В

…

и так n раз

…

Таким образом, было показано, что проведя эксперимент с утра и получив первым значение 99, 99 В (или чего-то другого), мы не можем быть уверены в том, что получим такое же значение после обеда (в другое время). Или, более обще: очень редко может случиться так, что мы получим два одинаковых результата в разное время.

Ну, и опять-таки видим тенденцию - все значения, полученные экспериментально асимптотически приближаются к ста вольтам.

100 Вольт

 

Случайные погрешности учитываются методами математической статистики.

Описание случайных погрешностей и понятие доверительного интервала

Из математической статистики известно, что случайная величина полностью описывается законами распределения. Есть интегральный и дифференциальный законы распределения, причём дифференциальный закон используется чаще в технике.

Обозначения: P(X) – плотность распределения вероятности

Пример 1:

Пусть измеряемая величина – X

P(X)

Дифференциальный закон распределения

Q – истинной значение X

 

0 X₁ Q X₂ X

Вероятность попадания (1-P) Вероятность попадания (1-P)

Вероятность попадания (Р)

Пусть, хотим знать будет ли результат «сидеть» в интервале

Пример 2: используется чаще

P(δ)

Закон распределения погрешности

 

 

δ₁ 0 δ₂ δ

На практике используют числовые параметры законов распределения или моменты.

Моменты:

1) Математическое ожидание M(X)

2) Дисперсия D(X)

 

Оценка мат. ожидания – это среднее значение измеряемой величины X при достаточно большом числе измерений n.

где n – число измерений, x_i – значение случайной величины.

В качестве характеристики отклонения среднего используется дисперсия:

Из-за своей размерности (невозможно сравнить дисперсию и мат. ожидание, так как у одной размерность X², а у другого – X) дисперсия на практике заменяется среднеквадратическим отклонением:

Таким образом получаем СКО с размерностью измеряемой величины и мат. ожидание с той же размерностью.

В измерительной технике пользуются понятием доверительного интервала погрешности.

 

Определение

Доверительный интервал погрешности – это те значения погрешности, за которые не выходит погрешность измеряемой величины с вероятность P_Д .

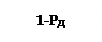
Доверительный интервал погрешности с доверительной погрешностью Р_Д

 

 

Причём,

Вероятность Р_Д попадания погрешности в свой доверительный интервал обычна довольно высока и составляет: от 0,8 до 0,(9).

Коэффициент k зависит от выбора закона распределения величины и доверительной вероятности попадания погрешности в интервал.

 

Поделиться:

Воспользуйтесь поиском по сайту: