Закон Генри. Закон Сивертса

Общие понятия и определения.

Химический потенциал компонентов раствора

К разбавленным растворам относятся растворы, которые удовлетворяют требованию:

 

Х₁ 1 и Х_i 0 или Х₁ >> X₂ (8.1)

 

где Х₁ – молярная доля растворителя;

Х_i – молярная доля растворённого вещества.

В разбавленном растворе молекулы растворённого вещества отделены друг от друга большим числом молекул растворителя. Поэтому в таком растворе отсутствует взаимодействие между молекулами растворённого вещества, а имеет место взаимодействие только между молекулами растворённого вещества и молекулами растворителя. Если к разбавленному раствору добавлять растворитель при постоянной температуре, то процесс разбавления будет протекать точно так же, как при добавлении растворителя к чистому растворителю. В этом случае с увеличением объёма раствора внутренняя энергия и энтальпия взаимодействия в системе растворитель – растворённое вещество не будет изменяться, т.е:

 

(8.2)

 

Как было показано раньше, уравнение (8.2) справедливо для идеального газа. Это означает, что между разбавленным раствором и идеальным газом существует аналогия. Так самопроизвольное распространение растворённого вещества по всему объёму растворителя аналогично расширению идеального газа в вакуум. Тогда при растворении одного моля растворённого вещества его парциальная молярная энтропия составит:

 

= , (8.3)

 

где S - член уравнения, учитывающий величины, не зависящие от С_i;

V – объём раствора;

С_i - молярная концентрация растворённого вещества.

Вследствие того, что в разбавленном растворе молекулы растворенного вещества отделены друг от друга большим числом молекул растворителя и не взаимодействуют друг с другом, то при добавлении молекул растворённого вещества к разбавленному раствору процесс сопровождается таким же изменением энтальпии, как и при добавлении молекул растворённого вещества к чистому растворителю. В этом случае парциальная молярная энтальпия растворённого вещества будет оставаться постоянной величиной и определится уравнением:

 

(8.4)

 

Тогда химический потенциал растворённого вещества в растворе составит:

 

μ_i = = = 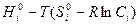(8.5)

 

или

μ_i = μ + RTlnC_i, (8.6)

где μ_i – химический потенциал растворённого вещества;

μ = H - TS - величина, зависящая только от температуры, имеющая

смысл химического потенциала растворённого вещества при его

концентрации в растворе, равной единице, при условии, что раствор

сохраняет свойства разбавленного или стандартного потенциала

растворённого вещества.

Уравнение Гиббса – Дюгема для одного моля разбавленного раствора, состоящего из n₁ молей растворителя и n₂ молей растворённого вещества, имеет вид:

Х₁d (8.7)

 

C учётом этого можно записать:

 

X₁dμ₁ + X₂dμ₂ = 0 (8.8)

 

Если концентрация какого – либо вещества мала, то его концентрации, выраженные через различные величины, пропорциональны друг другу. Тогда для растворённого вещества справедливо:

 

С₂ = kX₂ (8.9)

 

C учётом этого уравнение химического потенциала для растворённого вещества можно записать в виде:

 

μ₂ = μ 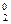+ RTln(kX₂) = μ 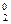+ RTlnk + RTlnX₂ = μ + RTlnX₂ (8.10)

 

где μ = μ 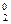+ RTlnk – постоянная, не зависящая от концентрации

растворённого вещества.

 

Тогда уравнение (8.8) можно записать в виде:

 

Х₁dμ₁ + X₂d(μ + RTlnX₂) = X₁dμ₁+ X₂RT = X₁dμ₁+ RTdX₂ (8.11)

 

Так как Х₁+Х₂ = 1, то dX₁ = -dX₂, тогда уравнение (8.11) можно представить в виде:

 

Х₁dμ₁ – RTdX₁ = 0 (8.12)

 

Откуда получим

 

dμ₁ = RT 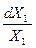= RTdlnX₁ (8.13)

 

Определённое интегрирование уравнения (8.13) даёт:

 

= (8.14)

 

или

μ₁= μ + RTlnX₁ (8.15)

 

где μ - химический потенциал чистого растворителя (Х₁ = 1).

Уравнение (8.15) представляет собой уравнение химического потенциала растворителя в разбавленном растворе.

Закон Генри. Закон Сивертса

Рассмотрим равновесие разбавленный раствор – пар. Для условий равновесия такой системы справедливо:

 

μ = μ , (8.16)

 

где μ - химический потенциал растворённого вещества в растворе;

μ - химический потенциал растворённого вещества в газовой фазе.

Считая пар растворённого вещества идеальным газом, можно записать:

 

μ + RTlnC_i = μ + RTlnP_i, (8.17)

 

где P_i – давление пара растворённого вещества над раствором.

 

После преобразования уравнения (8.17) получим:

 

ln = (8.18)

 

Величины, входящие в правую часть уравнения не зависят ни от концентрации растворённого вещества ни от давления его пара над раствором, а зависят только от температуры. Поэтому, если температура постоянна, то можно записать:

 

ln = Const или = Сonst = Г_i (8.19)

 

или

С_i = Г_i ·P_i (8.20)

 

где Г_i – постоянная Генри.

Уравнения (8.19) и (8.20) выражают закон Генри. Закон Генри гласит: концентрация растворённого вещества в жидкости пропорциональна давлению пара растворённого вещества над раствором.

Следует отметить, что закон Генри справедлив для растворения газа в молекулярных жидкостях.

При растворении многоатомных газов в твёрдых или расплавленных металлах и сплавах, растворённые в расплаве газы находятся в атомарном состоянии. Например, процесс растворения водорода в жидком металле можно выразить уравнением:

 

H_2(газ) = 2Н_(рас) (8.21)

 

Для условия равновесия в такой системе можно записать:

 

Δ = 2 = 0 (8.22)

 

или

2μ + 2RTlnC_H = μ + RTlnP (8.23)

 

После преобразования получим:

 

ln = (8.24)

 

Величины, входящие в правую часть уравнения не зависят ни от концентрации растворённого вещества ни от давления его пара над раствором, а зависят только от температуры. Поэтому, если температура постоянна, то можно записать:

 

ln = Const или = Сonst = Г (8.25)

 

или

С_Н = (Р Г ) (8.26)

 

Таким образом, для растворимости, водорода в расплавленном металле можно записать:

 

С_Н = г (Р ) (8.27)

 

где г = Г - постоянная Генри.

Уравнение (8.26) выражает закон Сивертса. Он гласит: растворимость газа в металлах и сплавах пропорциональна корню квадратному из давления газа над металлом.

В таком виде он справедлив для растворения двухатомных газов в твёрдых и расплавленных металлах и сплавах.

 

 

Закон Рауля

Рассмотрим равновесие разбавленный раствор – газ. Для условия равновесия такой системы справедливо:

 

μ_1(рас) = μ_1(газ) (8.28)

 

или

μ 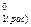+ RTlnX₁ = μ + RTlnP₁ (8.29)

 

После преобразования получим:

 

ln 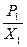= (8.30)

 

Величины, входящие в правую часть уравнения не зависят ни от концентрации растворённого вещества ни от давления его пара над раствором, а зависят только от температуры. Поэтому, если температура постоянна, то можно записать:

ln 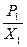= Const или 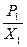= Сonst (8.31)

 

Выясним физический смысл постоянной величины. Если Х₁ = 1, то наша система будет представлять собой чистый растворитель. Тогда давление пара Р₁ будет представлять собой равновесное давление пара чистого растворителя Р или Const = P . Тогда уравнение (8.31) примет вид:

 

Р₁ = Х₁Р , (8.32)

 

где Р₁ – давление пара растворителя над раствором;

Р - давление пара растворителя над чистым растворителем;

Х₁ – молярная доля растворителя в растворе.

Поскольку для Х₁ всегда справедливо Х₁< 1, то из уравнения (8.32) следует, что Р₁ < P . Уравнение (8.31) выражает закон Рауля для растворителя в разбавленном растворе. Закон Рауля гласит: давление пара растворителя над раствором всегда меньше давления пара растворителя над чистым растворителем и пропорционально молярной доле растворителя в растворе.

Рассмотрим разбавленный раствор, состоящий из n₁ молей растворителя и n₂ молей растворённого вещества. Тогда молярные доли растворителя и растворённого вещества в растворе составят Х₁ и Х₂ соответственно. Поскольку Х₁ + Х₂ = 1 и Х₁ = 1 – Х₂, то уравнение (8.32) можно записать в виде:

Р₁ = (1 – Х₂)Р (8.33)

 

Преобразуя, получим

 

Х₂ = (8.34)

 

Уравнение (8.34) также представляет собой закон Рауля. В данном случае он формулируется следующим образом: относительное понижение пара растворителя над раствором равно молярной доле растворённого вещества.

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: