Преобразование одной фигуры в другую. Изменение количества квадратов в фигуре.

1. Пример

Цель. Упражнять детей в умении решать задачи путем целенаправленных практических проб и обдумывания хода решения.

Материал: счетные палочки у детей, у воспитателя - изображенные графически задачи (на этом и следующих занятиях).

Ход работы. 1. Воспитатель показывает детям таблицу с изображенной на ней фигурой, предлагает составить из палочек такую же (рис. 4). Рассматривает ее вместе с детьми, определяет количество квадратов. Затем говорит: "Это задача. Послушайте, что нужно сделать, чтобы решить ее. Надо догадаться, какие 4 палочки убрать, чтобы получился 1 прямоугольник. Сначала подумайте, как это можно сделать, а затем убирайте палочки".

После того как будет решена задача, воспитатель вызывает одного ребенка к доске, тот показывает и рассказывает, как нужно ее решить. Педагог одобряет попытки детей действовать самостоятельно.

2. Дана фигура из 6 квадратов. Надо убрать 2 палочки, чтобы осталось 4 таких же квадрата (рис. 5).

После составления детьми по образцу такой фигуры идет анализ по вопросам: "Сколько квадратов в фигуре? Как расположены? Как считаете, какие из палочек, образующих квадраты, надо убрать, чтобы сразу уменьшилось их количество?"

Дети самостоятельно решают задачу. Воспитатель в случае затруднения помогает им, ориентируя на поиск правильных способов.

2. Пример

Цель. Упражнять детей в умении осуществлять целенаправленные пробы, ограничивать количество практических проб за счет обдумывания хода поисков, догадки.

Ход работы. 1. Дана фигура из 5 квадратов. Надо убрать 3 палочки, оставив 3 квадрата (рис. 8). Воспитатель задает вопросы, побуждает детей к решению задачи: "Сколько квадратов в фигуре? Сколько должно остаться? Сколько палочек нужно убрать? Эта задача на смекалку, надо догадаться, какие 3 палочки нужно убрать, чтобы квадратов стало меньше - 3?"

Дети приступают к решению. Воспитатель напоминает о необходимости предварительного обдумывания хода поисков решения. В случае затруднения он напоминает условие задачи, предлагает не повторять пробных действий, которые не приводят к правильному решению.

Один из детей, решивших задачу в числе первых, зарисовывает и объясняет решение у доски.

2. Дана фигура из 4 равных квадратов. Надо убрать 2 палочки, чтобы получилось 2 неравных квадрата (рис. 9).

Вопросы для анализа составленной по образцу фигуры: "Сколько квадратов? Можете ли доказать, что они равны? Подумайте, как решить задачу".

По предложению воспитателя один ребенок объясняет у доски решение задачи.

3. Пример

Цель. Высказывать предположительный ход поиска решения, проверять его путем целенаправленных поисковых действий.

Ход занятия. 1. Дана фигура из 5 равных квадратов; надо убрать 4 палочки, чтобы стало 3 равных квадрата (рис. 13).

Воспитатель, обращаясь к детям, говорит: "Рассмотрите фигуру, подумайте, как можно решить задачу, какие из палочек убрать, чтобы изменилась эта фигура. Сначала расскажите, а потом убирайте палочки".

Воспитатель спрашивает некоторых детей (но так, чтобы их рассказы не слышали другие ребята), предлагает всем решить задачу самостоятельно. Дети объясняют решение задачи у доски, с тем, чтобы по ходу рассказа можно было сделать зарисовку фигур.

2. Дана фигура из 4 квадратов: надо переложить 2 палочки, чтобы получилось 5 равных квадратов (рис. 12).

Воспитатель после составления детьми фигуры и анализа задачи говорит детям, чтобы они, прежде чем переложить палочки, подумали, ведет ли это действие к увеличению количества квадратов, рассказали о том, как они думают решать задачу. В ходе проверки решения воспитатель подчеркивает, что решить задачу можно по-разному.

В процессе обучения на занятиях, дети 5-6 лет активно включаются не только в практический поиск решения, но и в умственный. Об этом свидетельствуют их высказывания, рассуждения о путях решения. Так, детям была дана фигура из 5 квадратов; надо убрать 4 палочки, чтобы осталось 3 таких же квадрата (рис. 14). Отвечая на вопрос воспитателя о том, как будут решать задачу, одни отвечают: "Я беру вот эти палочки (а, б и к) и эту (в). Что же тогда получится? (Задумывается.) Нет, не знаю как". Другие рассуждают: "Я думаю, что убрать надо 2 угловые палочки (е, ж) и еще где-то посмотреть надо". "Я догадалась. Посмотрела и догадалась: если эти убрать (показывает на г, д, и, з), то будет 3 квадрата: один, два, три".

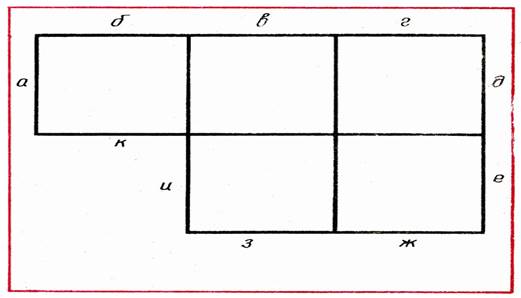
Рис. 14

В ходе выполнения заданий дети овладевают умением на основе обдумывания процесса поиска (анализа задачи) предполагать решение, проверять его практически, искать новые пути, обосновывать их.

Для обучения детей самостоятельному анализу задачи, поиску решения, умению догадываться целесообразно использование различных методических приемов, указаний о необходимости поискового подхода к решению задачи: "Сначала подумайте, как бы вы решили задачу, и расскажите об этом. Проверьте свое предположение, переложив палочки или даже не трогая их. Если считаете, что ошиблись, надо придумать, как решить задачу по-другому, а не повторять своих ошибок. Надо внимательно рассмотреть фигуру и догадаться, как решить задачу". Оценка, подтверждение правильности или ошибочности хода: "Эту палочку ты убрал правильно, подумай, как дальше решать задачу" - и другое стимулируют активность ребят, помогают им находить правильное решение.

В работе с детьми 7-го года жизни усложняется характер задач на преобразование фигур. Решаются они путем сочетания практических и мысленных проб или только в плане умственного действия - в уме, с обоснованием, выражением в речи хода решения.

Последовательность выполнения детьми 6-7 лет задач на преобразование фигур.

1. Переложить 1 палочку чтобы домик был перевернут в другую сторону (рис. 15).

Рис. 15

1. В фигуре, состоящей из 9 квадратов, убрать 4 палочки, чтобы осталось 5 квадратов (рис. 16).

Рис. 16

1. В фигуре из 6 квадратов убрать 3 палочки, чтобы осталось 4 квадрата (рис. 17).

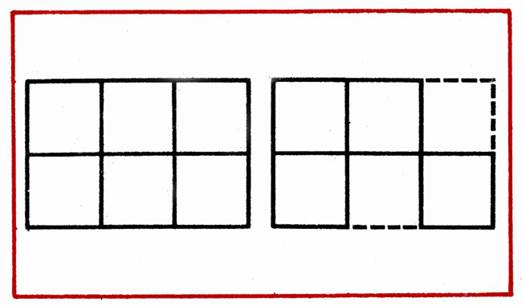
Рис. 17

1. В фигуре, похожей на ключ, переложить 4 палочки, чтобы получилось 3 квадрата (рис. 18).

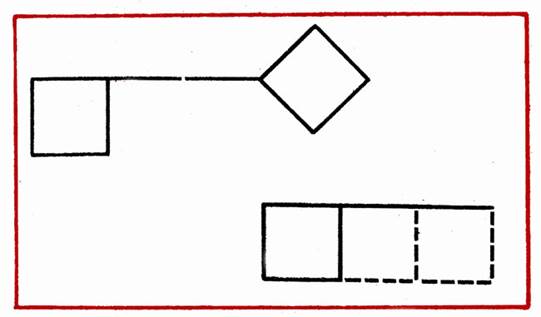
Рис. 18

1. В фигуре из 6 квадратов убрать 2 палочки так, чтобы осталось 4 равных квадрата (рис. 19).

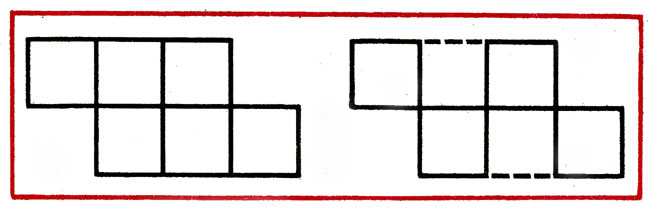
Рис. 19

1. В фигуре, изображающей стрелу, переложить 4 палочки так, чтобы получилось 4 треугольника (рис. 20).

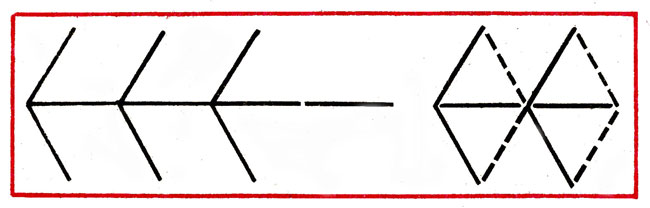
Рис. 20

1. В фигуре из 5 квадратов переложить 3 палочки, чтобы стало 4 квадрата (рис. 21).

Рис. 21

1. В фигуре переложить 3 палочки так, чтобы получилось 4 равных треугольника (рис. 22).

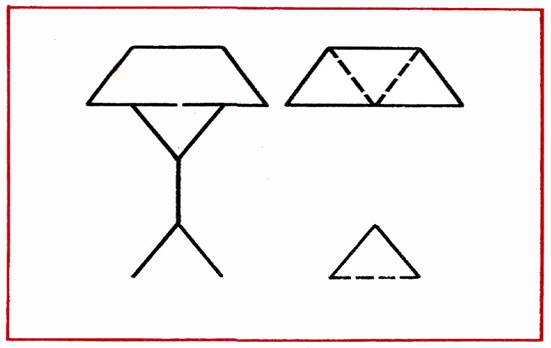
Рис. 22

1. В фигуре, состоящей из 4 квадратов, переложить 3 палочки так, чтобы получилось 3 таких же квадрата (рис.23).

Рис. 23

1. Переложить 4 палочки так, чтобы из топора получилось 4 равных треугольника (рис. 24).

Рис.24

1. В фигуре, напоминающей фонарь, переложить 4 палочки, чтобы получился четырехугольник, состоящий из 4 равных треугольников (рис. 25).

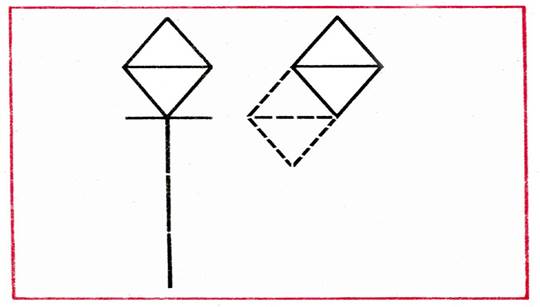
Рис. 25

1. Переложить 2 палочки так, чтобы фигура; похожая на корову, смотрела в другую сторону (рис. 26).

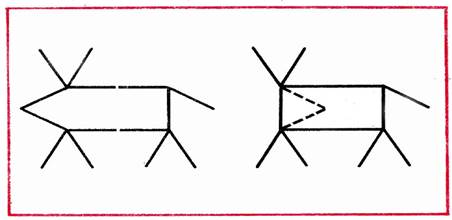
Рис. 26

1. Какое наименьшее количество палочек нужно переложить, чтобы убрать мусор из совочка? (рис. 27.)

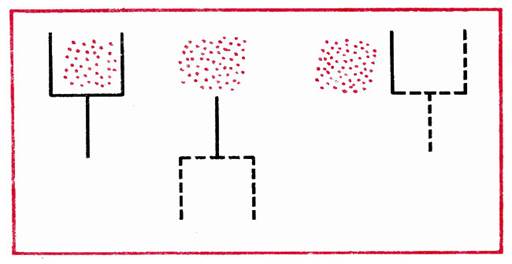
Рис. 27

В подготовительной к школе группе обучение детей решению задач на смекалку способствует дальнейшему развитию их умственной деятельности, способности планировать ход поисков.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: