Средние характеристики ряда динамики

Тема: Ряды динамики.

 

Основные понятия

Прогнозирование – это оценка будущего на основе глубокого анализа тенденций развития социально-экономических явлений и их взаимосвязей.

Оно ведется на основе широкого спектра информации. Первоначальный этап всегда связан с анализом временных рядов, то есть рядов динамики.

Опр.1. Ряд динамики – ряд последовательно расположенных во времени числовых значений, соответствующих показателю.

В ряде динамики существуют две величины:

t – моменты или периоды времени, к которым относятся приводимые статистические данные о изучаемом явлении (приводятся в первой графе)

y – статистические показатели, которые характеризуют данное явление на тот момент, который указан в первой графе.

 

Опр.2. Интервальные - это ряды, где уровни показывают развитие явления за определенные промежутки или интервалы времени (данные могут быть суммированы).

Устно: Можно, например от данных динамики по месячной выплавке стали к данным по годовой выплавке стали, суммируя месячные уровни.

Замечание1. Можно дробить уровни ряда и определять их значения за малый интервал времени.

Суммируя уровни рядов из абсолютных величин можно строить ряды с нарастающими итогами.

Опр.3. Моментные - это ряды, где уровни характеризуют состояние явлений на определенные даты или моменты времени (данные не могут быть суммированы).

Замечание.2. Уровни моментного динамического ряда не меняются с изменением временных промежутков.

Опр.4. Рядом динамики абсолютных величин   называется ряд, уровни которого можно суммировать во времени, то есть переходить от ряда динамики с малыми временными интервалами к более крупным промежуткам времени.

Опр.5. Рядом динамики относительных величин называют ряд цифровых данных, характеризующих изменение относительных размеров общественных явлений во времени.

Опр.6. Рядом динамики средних величин называется ряд цифровых данных, характеризующих изменение средних размеров признаков общественных явлений во времени.

Замечание.3. Если прогнозирование проводить на основе одного изолированного ряда, то основной задачей будет выявление тенденции в изменении уровней ряда, что можно использовать в экстраполяции.

Экстраполяция – это одна из вариантов окончательного прогноза.

Период на который дается оценка будущего, называется период упреждения. Прогнозные оценки основываются в предположении, что тенденции – стабильные.

Сопоставимость рядов динамики

При использовании временных рядов исследователю приходится решать вопрос, связанный с сопоставимостью уровней динамического ряда. Числовые значения показателей должны быть сравнимы по разным временным интервалам. Несопоставимость может быть обусловлена изменением:

1. состава изучаемой совокупности;

2. границ территории;

3. цен стоимостных показателей;

4. методологии расчета показателей;

5. единиц измерения (при деноминации рубля);

6. различной продолжительностью интервалов времени к которым относятся уровни.

Существуют специальные приемы приведения уровней ряда динамики к сопоставимому виду. Один из них называется смыканием рядов динамики. Суть его состоит в том, что в год изменения методологии расчета уровень ряда приводится в двойной оценке: по прежней новой методике (или в старых и новых границах при территориальных изменениях). Это позволяет найти соотношение уровней и на его основе пересчитать уровни прошлых лет.

Пример

Год	2013	2014	2015	2016	2017	2018
Объем реал_прод_ 10 предпр_млн.руб	120	125	130	140
Объем реал_прод_ 12 предпр_млн.руб	-	-	-	168	180	196
Сопоставимый ряд	144	150	156	168	180	196

 

Коэффициент сопоставимости = 168/140=1,2

Любой прогноз начинается с изучения аналитических показателей динамики. Которые раскрывают в каком направлении изменяются уровни ряда динамики и с какой интенсивностью.

Таким образом, основные задачи, возникающие при изучении рядов динамики:

1. характеристика интенсивности отдельных изменений в уровнях ряда от периода к периоду или от даты к дате;

2. определение средних показателей временного ряда;

3. выявление закономерностей динамического ряда в целом;

4. интерполяция и экстраполяция;

5. выявление факторов, обуславливающих изменение изучаемого явления.

 

Сопоставляя между собой ряд последовательных уровней, можно получить характеристику скоростей и интенсивности развития явлений.

Показатели ряда динамики:

1. абсолютный прирост;

2. коэффициент роста;

3. темп роста

4. абсолютное значение одного процента прироста

Возможно два варианта сопоставления:

1.Каждый уровень сравнивают с одним и тем же уровнем (с постоянной базой).

2. Каждый уровень сравнивают с предыдущим уровнем (с переменной базой).

Абсолютный прирост ∆yi определяется как разность между двумя уровнями динамического ряда и показывает, насколько единиц уровень одного периода больше или меньше уровня, взятого за базу сравнения.

∆y_б = y_i - y_б                                                                                                             (2)

где ∆y_б абсолютный, базисный прирост;

у_i – уровень сравниваемого периода

у_б – уровень базисного периода.

При сопоставлении с переменной базой абсолютный прирост будет равен:

∆y_ц = y_i – y_i-1                                                                                                          (3)

где y_i-1 – уровень непосредственно предшествующего периода.

Цепной абсолютный прирост иногда называется скоростью роста.

 

Интенсивность изменения уровней характеризуется коэффициентами роста, темпами роста и темпами прироста.

Коэффициент роста определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень базисного периода.

 при сравнении с постоянной базой                                                     (4)

 при сравнении с переменной базой                                                   (5)

Темпами роста называют коэффициенты роста, выраженные в процентах:

Т_ц=К_ц×100%  и  Т_баз=К_баз×100%                                                                   (6)

Между темпами роста существует взаимосвязь.

1.Произведение цепных темпов роста дает базисный темп за весь период

Т_ц1×Т_ц2×…×Т_цn=T_бn                                                                                                                                                            (7)

2.Частное от деления последующего базисного темпа на предыдущий, дает темп цепной

                                                                                                                 (8)

Темп прироста показывает, на сколько процентов уровень данного периода отличается от базисного или предыдущего уровня. Этот показатель может быть рассчитан двумя способами:

1.как отношение абсолютного прироста к базисному уровню

T∆_баз= 100%   или T∆_цеп= 100%                                                    (9)

2.как разность между темпом роста в процентах и 100%

T∆_баз = Т_баз - 100% или T∆_цеп = Т_цеп - 100%                                                        (10)

Чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением 1% прироста А_i. Он рассчитывается как отношение абсолютного прироста к темпу прироста (в %) за тот же период времени.

                                                                                                                 (11)

                                                                        (12)

1% - сотая часть достигнутого уровня в предыдущем периоде.

Если абсолютные приросты систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как:

∆^// = ∆_i - ∆_i-1

Если растут цепные темпы роста, то ряд развивается с относительным ускорением.

 

Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:

∆% = Тi – Тi-1  или  ∆% = ∆Тi - ∆Ti-1

 

Пункт роста или снижения. В тех случаях, когда сравнение производится с отдельным периодом времени, принятого за базу сравнения, рассчитывают пункты роста или снижения, которые представляют собой разность базисных темпов роста (в %) двух смежных периодов.

                                                       (13)

Пункты роста можно складывать, в результате чего получаем темп прироста соответствующего периода по сравнению с базисным периодом.

При сопоставлении динамики развития двух явлений, можно использовать коэффициент опережения. С его помощью сравниваются динамические ряды одинакового содержания, но относящиеся к разным территориям или организациям; или ряды разного содержания. Характеризующие один объект.

                                                                          (14)

где у^/ и y^// - соответствующие уровни сравниваемых динамических рядов.

 

Средние характеристики ряда динамики

Для интервального ряда абсолютных показателей средний уровень за период определяется по формуле простой средней арифметической:

                                                                                                               (15)

где n – число уровней ряда

Для определения среднего уровня неравноинтервального ряда используется средняя арифметическая взвешенная:

                                                                                                             (16)

где t_i – величина интервала.

Средний уровень моментного динамического ряда определяется по средней хронологической:

                                                                                 (17)

где n – число дат;

у₁, у₂, …, у_n -  уровни ряда в последовательные моменты времени.

Средний уровень моментного ряда с неравными промежутками между датами вычисляется по формуле:

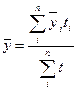                                                                                                              (18)

где t_i – количество дней, месяцев между смежными датами;

- средний уровень между двумя соседними датами.

Средний абсолютный прирост (или средняя скорость роста) рассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:

                                                                                            (19)

Средний годовой темп роста вычисляется по формуле средней геометрической из показателей темпов роста за отдельные периоды:

    (средняя геометрическая простая)                      (20)

Средний годовой темп прироста определяется на основании данных о среднегодовых темпах роста. Он показывает на сколько процентов изменяется в среднем уровень ряда

                                                                                           (21)

Поделиться:

Воспользуйтесь поиском по сайту: