Метод отсекающих плоскостей

Лабораторная работа №5

Методы принятия решений в условиях определенности

Задачи дискретного программирования

 

Модели целочисленного (дискретного) программирования в области экономики и управления включают в себя задачи, в которых на искомые переменные накладываются условия целочисленности, а также область допустимых решений этих задач конечна.

Методы решения задач дискретного программирования де­лятся на 3 группы: 1) метод отсекающих плоскостей; 2) комби­наторные методы (например, метод ветвей и границ); 3) метод случайного поиска и эвристические методы.

Метод отсекающих плоскостей

Метод отсекающих плоскостей предназначен для решения частного случая задач дискретного программирования – задач линейного целочисленного программирования. В литературе этот метод встречается также под названиями: метод отсечения, или метод Гомори.

Метод состоит в следующем. Сначала отыскивается опти­мальный план без учета условия целочисленности. Если полу­ченный план целочисленный, то решение получено, а если – нет, то формируем дополнительное ограничение, называемое правильным отсечением, которому заведомо удовлетворяет лю­бое целочисленное и не удовлетворяет найденное оптимальное нецелочисленное решение. Это дополнительное ограничение присоединяется к исходным ограничениям задачи, затем вновь отыскивается оптимальный план и т.д.

Правильное отсечение должно обладать следующими свой­ствами:

1) быть линейным;

2) отсекать найденный оптимальный нецелочисленный план;

3) не отсекать ни одного целочисленного плана.

В общем случае алгоритм Гомори будет следующим. Надо решить задачу линейного целочисленного программи­рования:

(1.6.1)

при ограничениях

	(1.6.2)
	(1.6.3)
– целые,	(1.6.4)

Если исходная система ограничений совместна и функция ограничена на множестве решений, то отыскиваем оптимальное решение, отбросив условие целочисленности.

Допустим, что найденный оптимальный план не является це­лочисленным, например, для 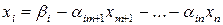, где основные переменные, 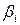– не­целая компонента. Тогда для i -й переменной, имеющей нецело­численное значение, формируем дополнительное ограничение, которое имеет вид

,

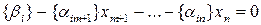(1.6.5)

где { } – дробная часть значения.

Замечание. Дробная часть свободного члена берется с тем же знаком, который он имеет в уравнении, а дробные части коэффи­циентов при неосновных переменных берутся с противоположными знаками.

После этого дополнительное ограничение приводим к кано­ническому виду:

,

включаем это соотношение в систему ограничений (1.6.2) и сно­ва ищем оптимальный план и т.д.

Таким образом, дополнив исходную систему ограничения (1.6.2) правильным отсечением (1.6.5), отыскиваем оптимальное решение новой задачи Л П. Если дополнительное ограничение сформулировано правильно, то через несколько итераций будет найдено искомое решение задачи линейного целочисленного программирования, либо мы установим ее неразрешимость.

Пример. Найти F= 2х₁ + 3х₂ ® max

при условиях

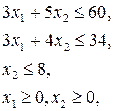
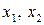– целые.

Отбрасывая условия целочисленности, находим симплекс-ме­тодом решение данной задачи. Получаем решение

; .

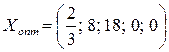Данное решение не удовлетворяет условию целочисленности, поэтому формируем правильное отсечение для базисной пере­менной x₁ которая определяется как

.

Дополнительное ограничение будет иметь вид

.

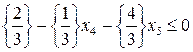После преобразования данного ограничения и приведения его к каноническому виду получим

.

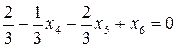Данное уравнение необходимо включить в систему ограни­чений исходной задачи, записанной в каноническом виде, и повторить ее решение и т.д. В результате получим следующее решение исходной задачи:

; .

 

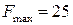Метод ветвей и границ

Метод состоит в последовательном ветвлении исходного мно­жества решений на дерево подмножеств с поиском решений на всех подмножествах, пока не будет найдено необходимое.

Пусть требуется решить задачу

(1.6.6)

при ограничениях

	(1.6.7)
	(1.6.8)
– целые,	(1.6.9)

Искомое решение задачи (1.6.6)–(1.6.9) будет найдено на множестве, соответствующем висячей вершине с максимально возможной оценкой. Множество, на котором получено опти­мальное целочисленное решение, ветвлению не подлежит. Ему соответствует концевая, или висячая, вершина дерева решений.

Как и в методе отсекающих плоскостей, процесс начинается с решения непрерывной задачи линейного программирования без учета целочисленности. Если полученный оптимальный ре­зультат Х_опт не удовлетворяет условию (1.6.9), то значение целе­вой функции дает верхнюю оценку искомого решения на мно­жестве G, заданном условиями (1.6.7)–(1.6.8). При этом если имеется некоторая нецелочисленная переменная, то в целочис­ленном плане ее следует либо уменьшить до значения 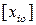, либо увеличить до [ х_i0 ] + 1, т.е. из области допустимых решений исключается область [ х_i0 ] <x_i0< [ х_i0 ] + 1. Тем самым из исходной задачи формируются две задачи: 2 и 3, отличающиеся друг от друга тем, что в задаче 2 кроме ограничений (1.6.7)–(1.6.8) исходной задачи добавлено ограничение х_i0 < [ х_i0 ], а в задаче 3 кроме ограничений (1.6.7)–(1.6.8) исходной задачи добавлено ограничение [ x_i0 ] + 1 < x_i0.

Таким образом, исходное множество G разбивается на два непересекающихся подмножества:

,
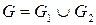,	(1.6.10)
.	(1.6.11)

Находим решения и оценки на множествах (1.6.10) и (1.6.11). Если решения, полученные на G₁ и G₂, – целочисленные, то оптимальным планом будет тот, у которого целевая функция бу­дет максимальной. Если на множестве G₁ получено целочислен­ное решение, а на G₂ – нецелочисленное, но значение целевой функции на множестве G, будет больше значения целевой функ­ции на множестве G₁ то продолжаем ветвление множества G₂, так как на следующем этапе мы можем получить целочисленное решение, оценка которого будет больше, чем оценка целевой функции на множестве G₁.

Построение дерева решений продолжается до тех пор, пока не будет найдено решение задачи (1.6.6)–(1.6.9), полученное на множестве, соответствующем висячей вершине с максимально возможной оценкой.

Пример. Найти

(1.6.12)

при условиях:

,	(1.6.13)
,	(1.6.14)
,	(1.6.15)
– целые.	(1.6.16)

Приведем алгоритм решения.

Шаг 0. Отбросив условие целочисленности и приведя ограни­чения к каноническому виду, любым методом отыскиваем оп­тимальное решение на исходном множестве (7°, определяемом ограничениями (1.6.13)–(1.6.15).

Для рассматриваемого примера получим следующее решение:

, ; .

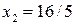Так как решение нецелочисленное, переходим к следующему шагу.

Шаг 1. Разбиваем исходное множество G на 2 подмножества

,

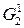и находим решение и оценки на этих множествах. Для отыска­ния решения на множествах и дописываем ограничения и найденному на множестве G⁰ решению. Для это­го дополнительные ограничения представим также в каноничес­ком виде и дописываем их к исходным (1.6.13)–(1.6.15):

,

.

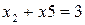Решаем полученную задачу с учетом новых ограничений. В нашем примере полученное множество 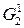будет пустым и оцен­ка его равна ¥. Оценка же на множестве : , , , .

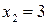Шаг 2. Разбиваем множество на два подмножества и :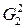

.

Поступив так же, как и на первом шаге, дописываем новые ограничения 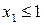и 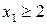к ограничениям множества , пред­ставив их в каноническом виде:

Решаем полученную задачу. В результате данного шага полу­чим следующие решения:

– решение на множестве : – удовлетворяет условию целочисленности;

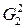– решение на множестве : , – не удовлетворяет условию целочисленности и его оценка больше чем на множестве . Поэтому будем раз­бивать это множество дальше.

Шаг 3. Разбиваем множество 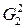на два подмножества:

Аналогично, как и в предыдущих шагах, дописываем новые ограничения и к найденному на множестве 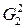реше­нию, предварительно представив их в каноническом виде. Получим следующее решение на множестве : , , , , , , 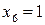которое удовлетворяет условию целочислен­ности. Дальнейшие вычисления прекращаются, так как не мо­жет быть решения с лучшей оценкой. Задача решена: Z= 12, .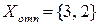

 

Решение дискретных задач

Поделиться:

Воспользуйтесь поиском по сайту: