Перестановки с повторениями

Сочетания

В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений. Число сочетаний из n элементов по k обозначаются 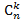Так, например, наборы (3-элементные сочетания, подмножества, k = 3) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n = 6) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}. В общем случае число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k -й диагонали и n -й строки треугольника Паскаля. если кортежи имеют одинаковый состав, то такие картежи называются эквивалентными. На сколько классов эквивалентности тогда разбивается при этом вся совокупность кортежей длины из n элементов Эти классы и будут называться сочетаниями с повторениями из n элементов по k а их число обозначают .

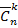Основные формулы:

Формула №1

 

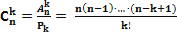при

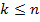
Доказательство:

Вычисляя число размещений, мы получим пары, отличающиеся порядком элементов, Из двух элементов можно составить две перестановки упорядоченных пар, поэтому 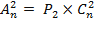, так как число размещений , умноженному на число перестановок внутри группы 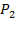. Для любого количество размещений из n элементов поk можно вычислить по формуле 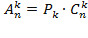. Действительно из n элементов можно составить групп по k элементов, а в каждой группе можно выполнить 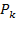перестановок. Таким образом число всех размещений 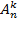равно произведению числа групп 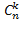и числа перестановок внутри этих групп Отсюда следует что ч.т.д.

Формула № 2

 

 

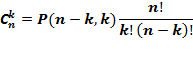
Вывод формулы:

 

 

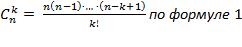
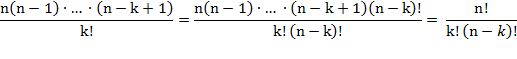
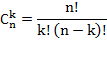
Формула №3

 

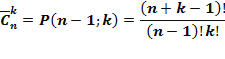
Доказательство: Любой состав кортежа длины k из n элементов имеет вид, 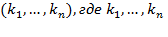— неотрицательные целые числа, сумма которых равна k. Заменяя каждое из чисел k, соответствующим количеством единиц о разделяя пулями единицы, отвечающие различным числам, получаем кортеж из n — 1 нулей и k единиц. При этом каждому составу отвечает одна и только одна запись с помощью нулей и единиц, а каждая такая запись задает один и только один состав. Поэтому число различных составов равно числу перестановок с повторениями из n — 1 нулей и k единиц, т. е. .
Примеры задач:

Зaдача № 1Извесно, что имеется 13 983 810 различных способов заполнения карточки "Спортлото", а выиграли номера 1, 2, 3, 4, 5,6. Сколько лиц выиграли в эту игру?

Решение: Угадать все: удастся только 1так как 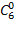=1Запишем пары, на первом месте которых стоит один из 6 заменяемых номеров, а на втором — тот номер, которым он заменяется.

(1,7),(1,8)...(1,49)

(2,7),(2,8)...(2,49)

…………………….

(6,7),(6,8)... (6,49)

Пара (1, 7) обозначает, что вместо правильной комбинации {1, 2, 3, 4, 5, 6} участник лотереи зачеркнул номера {7, 2, 3, 4, 5, 6}, угадав лишь 5 номеров. Из таблицы видно, что число возможностей ошибиться один и только один раз равно 6×43 = 258. Значит, 258 участников угадают 5 номеров. Таким же образом мы определяем, что 4 номера угадают 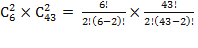=13 545 человек — сначала надо из 6 верных номеров выбрать какие-нибудь 2 (это делается 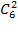способами), а затем заменить их парой номеров, выбранной из 43 несчастливых номеров (а это можно сделать 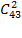способами).Комбинируя каждый способ выбора первой пары с каждым способом выбора заменяющей ее пары, тогда совпадут 3 цифры у 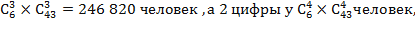одна цифра у 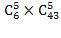человек и не одной цифры у .

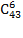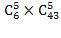Ответ угадает всё -1 угадает 5 цифр – 258, угадает 4цифры – 13 545, угадает 3- 246 820, угадают 2 цифры - человек, 1 цифру- , не угадает не одной .

Задача№2 Путник хочет попасть из пункта А в пункт В кратчайшим путем, т. е. двигаясь все время или "слева направо", или "снизу вверх". Сколькими путями он может добраться из А в В?

Решение. Ясно, что, каким бы путем ни шел путник, он пройдет через (n + k) перекрестков (считая точку А, но не считая точки В). На каждом перекрестке он может идти или направо, или вверх. В соответствии с этим все перекрестки делятся на два класса: "перекрестки направо" и "перекрестки вверх". При этом направо путник идет k раз, а вверх n раз. Значит, чтобы однозначно восстановить его путь, надо знать лишь те k случаев, когда он идет направо. Но их можно выбрать из общего числа (n + k) перекрестков 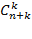способами. Поэтому число искомых путей равно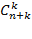
Треугольник Паскаля

Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух, расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси^[1]. Имеет применение в теории вероятности и обладает занимательными свойствами.

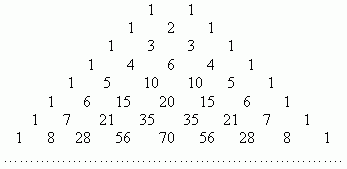
Свойство треугольника:

Свойство№1

 

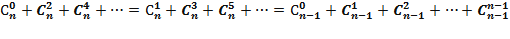
При составлении арифметического треугольника каждое число n-й строки участвует в образовании двух чисел (n + 1)-й строки — стоящего слева и стоящего справа от него. Поэтому если сложить числа (n + 1)-й строки через одно, то в полученную сумму войдут по одному разу все числа n-й строки. Складывать числа через одно можно двумя способами — начав с первого числа строки или начав со второго числа. В обоих случаях получится одна и та же сумма, равная сумме чисел в n-й строке. Следовательно

 

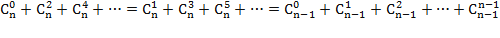
Свойство№2 (следствие из свойства№1)

 

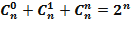
Из свойства№1следует, что сумма чисел (n + 1)-й строки вдвое больше суммы чисел n-й строки. Иными словами, при переходе к следующей строке арифметического треугольника сумма чисел в строке удваивается. Но в первой строке стоит только одно число 1, а потому для нее сумма равна 1. Поэтому в (n + 1)-й строке сумма чисел равна 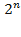. следовательно:

 

Размещения без повторений
Размещения без повторений из n элементов по m – это упорядоченные m-множества, состоящие из n- множества
Общий вид задач:
Имеется n различных предметов. Сколько из них можно составить расстановок? При этом две расстановки считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.
Такие расстановки называют размещениями без повторений. При составлении k -размещений без повторений из n предметов нужно сделать k выборов. На первом шагу можно выбрать любой из имеющихся n предметов. Если этот выбор уже сделан, то на втором шагу приходится выбирать из оставшихся n-1 предметов - ведь повторный выбор сделать уже нельзя. Точно так же на третьем шагу для выбора остается лишь (n-2) свободных предметов, на четвертом - n-3 предметов... на k -ом шагу (n-k+1) предметов. Поэтому по правилу произведения получаем, что число k -размещений без повторения из n предметов выражается следующим образом:

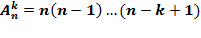
Пример. Нужно выбрать президента общества, вице - президента, ученого - секретаря и казначея. Сколькими способами может быть сделан это выбор, если каждый член общества может занимать лишь один пост?
В этом случае нужно найти число размещений(без повторений) из 23 элементов по 4. Ведь здесь играет роль, кто будет выбран в руководство общества и то, какие посты займут выбранные (выбор: президент – Иванов, вице-президент - Татаринов, ученый секретарь - Тимошенко, казначей – Алексеев, отличается от выбора: президент – Тимошенко, вице-президент – Иванов, ученый- секретарь – Татаринов, казначей - Алексеев). Поэтому ответ дается формулой
Перестановки без повторений
Перестановкой из 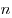элементов (или 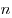-перестановкой) называется размещение из 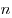элементов по 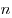без повторений.
Число перестановок из 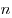элементов без повторений обозначается 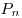от французского слова perturbation.
Теорема: число способов расположить в ряд 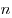различных объектов есть

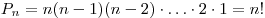Пример. Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?
Решение: Найдем количество всех перестановок из этих цифр: P₆=6!=720
0 не может стоять впереди числа, поэтому от этого числа необходимо отнять количество перестановок, при котором 0 стоит впереди. А это P₅=5!=120.
P₆-P₅=720-120=600
Сочетания без повторений
Сочетанием без повторений из 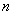элементов по называется неупорядоченное -элементное подмножество 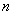-элементного множества. Число сочетаний без повторений из 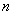элементов по равно :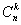

Например, требуется подсчитать, сколькими способами можно составить бригаду из трех человек для дежурства в группе из 30 человек. Поскольку порядок расположения людей в бригаде не фиксируется и люди не повторяются, то мы имеем случай сочетаний из 30 элементов по 3 без повторений:

.

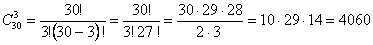Таким образом, бригаду дежурных из трех человек в группе из 30 человек можно выбрать 4060 различными способами.

Размещения и сочетания с повторениями
Часто в задачах по комбинаторике встречаются множества, в которых какие-либо компоненты повторяются. Например: в задачах на числа – цифры. Для таких задач при размещениях используется формула 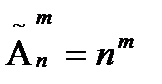, а для сочетаний .
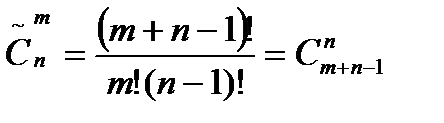Пример. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?

Решение. Так как порядок цифр в числе существенен, цифры могут повторяться, то это будут размещения с повторениями из пяти элементов по три, а их число равно .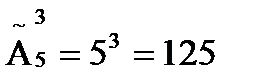

 

В кондитерском магазине продавались 4 сорта пироженных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно купить 7 пироженных.

Решение: Покупка не зависит от того, в каком порядке укладывают купленные пироженные в коробку. Покупки будут различными, если они отличаются количеством купленных пирожных хотя бы одного сорта. Следовательно, количество различных покупок равно числу сочетаний четырех видов пироженных по семь - .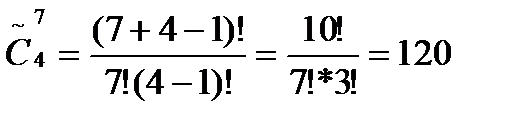

Обезьяну посадили за пишущую машинку с 45 клавишами, определить число попыток, необходимых для того, чтобы она наверняка напечатала первую строку романа Л.Н. Толстого «Анна Каренина», если строка содержит 52 знака и повторений не будет
Решение: порядок букв имеет значение. Буквы могут повторяться. Значит, всего есть вариантов.

Перестановки с повторениями

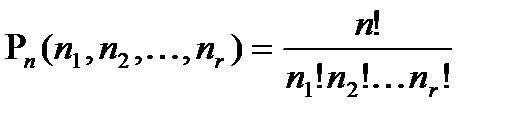
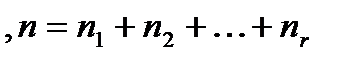, где n-количество всех элементов, n₁,n₂,…,n_r-количество одинаковых элементов.
Пример. Сколькими способами можно переставить буквы слова «ананас»? Решение: всего букв 6. Из них одинаковы n₁«а»=3, n₂«н»=2, n₃«с»=1. Следовательно, число различных перестановок равно .

Задачи для самостоятельного решения
Задача №1 Чемпионат России по шахматам проводится в один круг. Сколько играется партий, если участвуют 18 шахматистов?
Задача № 2 У людоеда в подвале томятся 25 пленников. а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? Порядок важен. б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?

Задача № 3 Рота состоит из трех офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20рядовых

Задача №4 Сколькими способами можно разбить 10 человек на две баскетбольные команды по 5 человек в каждой?

Задача №5 а) Из класса, в котором учатся 30 человек, нужно выбрать двоих школьников для участия в математической олимпиаде. Сколькими способами это можно сделать? б) Сколькими способами можно выбрать команду из трех школьников в том же классе?

Задача №6 В парламенте 30 депутатов. Каждые два из них либо дружат, либо враждуют, причем каждый дружит ровно с 6 другими. Каждые 3 депутата образуют комиссию. Найдите общее число комиссий, в которых все три члена попарно дружат или все трое попарно враждуют.

Задача№7 Сколькими способами можно выбрать четырех человек на четыре различные должности, если имеется девять кандидатов на эти должности?

Задача №8 В школе изучают 2n предметов. Все ученики учатся на 4 и 5. Никакие два ученика не учатся одинаково, ни про каких двух нельзя сказать, что один из них учится лучше другого. Доказать, что число учеников в школе не больше . (Мы считаем, что ученик p учится лучше ученика q, если у p оценки по всем предметам не ниже, чем у q, а по некоторым предметам – выше.)

Задача №9 Имеется 20 человек – 10 юношей и 10 девушек. Сколько существует способов составить компанию, в которой было бы одинаковое число юношей и девушек?

Задача №10 Международная комиссия состоит из 9 человек. Материалы комиссии хранятся в сейфе. Сколько замков должен иметь сейф, сколько ключей для них нужно изготовить и как их разделить между членами комиссии, чтобы доступ к сейфу был возможен тогда и только тогда, когда соберутся не менее 6 членов комиссии?

Список литературы
1.Учебное пособие по математике для поступающих в вузы под редакцией Г.Н. Яковлева -1981
2. Раизер Г. Дж. "Комбинаторная математика"
3.. Семеновых А. "Комбинаторика" //Математика. – 2004
4..http://combinatorica.narod.ru/second.htm

 

 

 

Поделиться:

Воспользуйтесь поиском по сайту: