 |
Амплитудный и фазовый спектр
|
|
|
|
Амплитудный спектр непериодического сигнала – зависимость модуля спектральной плотности амплитуд от частоты:
 (7)
(7)
Воспользовавшись графопостроителем [Л4], построим амплитудный спектр (см. рис. 3).

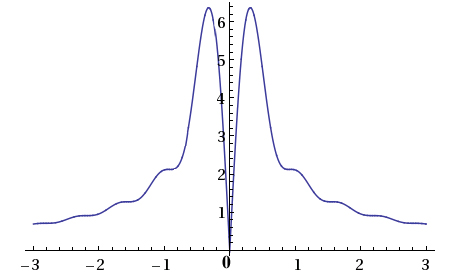

Рис. 3. Амплитудный спектр непериодического сигнала (1)
Учитывая, что мнимая единица, входящая в (6), есть  , то фазовый спектр определим следующим образом:
, то фазовый спектр определим следующим образом:
 (8)
(8)
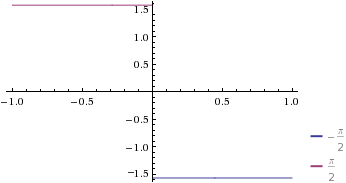
Построим график фазового спектра (рис. 4).
0 
Рис. 4. Фазовый спектр нереодического сигнала (1)
На основе полученных данных сделаем выводы об спектре одиночного видеоимпульса:
· Спектр сплошной
· Спектр двухсторонний
· Спектр бесконечный
· Спектр есть четная функция
· Фазовый спектр представляет собой сплошную,бесконеную, двухстороннюю и нечетную функцию.
Раздел 2
Спектральный анализ периодического сигнала
Имеется одиночный импульс S(t) (см. рис. 1). Его спектральная функция определяется путем применения к S(t) прямого преобразования Фурье:
 (9)
(9)
Путем повторения данного импульса через интервал T образуем периодическую последовательность импульсов S(t±kT), k=1,2,3…. Ее спектр может быть вычислен как:
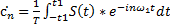 , (10)
, (10)
где  .
.
Сравнивая формулы (9) и (10) приходим к соотношению, устанавливающею связь между спектрами одиночного импульса и периодической последовательности импульсов:
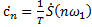 (11)
(11)
где 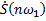 - значение спектральной функции импульса на частоте ω=
- значение спектральной функции импульса на частоте ω= 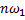 . Запишем выражение (11) в виде
. Запишем выражение (11) в виде
 (12)
(12)
Равенство (12) распадается на два равенства, которые устанавливают связь между спектрами одиночного импульса и периодической последовательности импульсов:
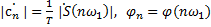 . (13)
. (13)
Зная спектральную плотность одиночного импульса (6), период повторения Т=5*t1 и воспользовавшись формулой (11) получим:
|
|
|
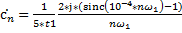 . (14)
. (14)
Используя соотношения (13) определим фазовый и амплитудный спектр:
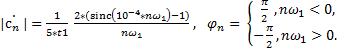 , (15)
, (15)
 [B*c]
[B*c]
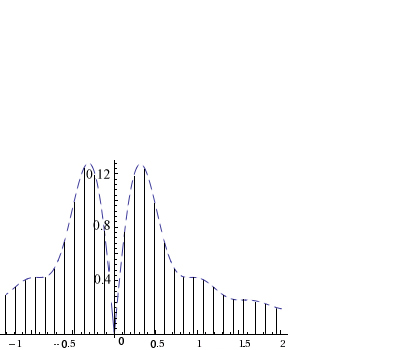

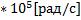
Рис. 5. Амплитудный спектр периодического сигнала.
На (рис. 5) изображен спектр периодической последовательности импульсов, анализировав его можно прийти к выводам, что:
· Спектр бесконечный
· Спектр дискретен
· Спектр двухсторонний
Раздел 3
Спектральный анализ непериодического радиоимпульса
Радиоимпульс - это высокочастотное колебание, огибающая которого имеет форму заданного видеоимпульса. Если S(t) – заданный импульс, то ему соответствует радиоимпульс:

S(t)= 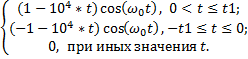 (16)
(16)
При этом функцию S(t) называют огибающей радиоимпульса [Л3], а функцию 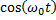 – его заполнением;
– его заполнением; 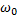 - частота заполнения, выбор которой обусловлен условием:
- частота заполнения, выбор которой обусловлен условием:
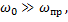 (17)
(17)
где 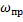 – практическая ширина спектра заданного видеоимпульса, определяемая уровнем 0,1 от максимального уровня сигнала.
– практическая ширина спектра заданного видеоимпульса, определяемая уровнем 0,1 от максимального уровня сигнала.
Найдем максимальный уровень сигнала используя online – сервис для математических расчетов Wolfram | Alpha Examples [Л4]: 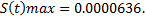
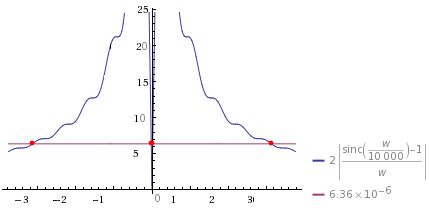
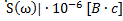
Рис. 6. Практическая ширина спектра.
Найдем практическую ширину спектра. Для это узнаем частоту соответствующую уровню 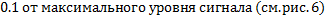 . Воспользовавшись снова сервисом математических расчетов [Л4] получаем
. Воспользовавшись снова сервисом математических расчетов [Л4] получаем 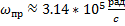
Возьмем 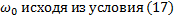 на порядок выше практической ширины:
на порядок выше практической ширины: 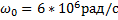 .
.
Из теоремы смещения спектра Фурье следует, что умножение сигнала на функцию 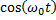 соответствует смещение его спектра по оси частот на
соответствует смещение его спектра по оси частот на  вправо и на -
вправо и на - 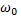 влево. Спектр как бы «раздваивается», при этом уровень спектра уменьшается в два раза:
влево. Спектр как бы «раздваивается», при этом уровень спектра уменьшается в два раза:
 (18)
(18)
где 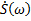 - спектральная плотность видеоимпульса.
- спектральная плотность видеоимпульса.
Применим формулы (18) и получим спектральную плотность непериодического радиоимпульса:

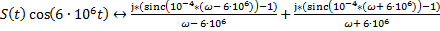 (19)
(19)
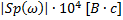

 рад/с
рад/с
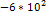 0
0 
Рис. 7 Амплитудный спектр непериодического радиоимпульса
Проанализировав полученные данные, можно сделать выводы, что спектр одиночного радиоимпульса представляет собой спектр одиночного видеоимпульса, но «раздвоенного» и перенесенного в область высоких частот ±  Спектр непрерывный.
Спектр непрерывный.
|
|
|
Раздел 4
Спектральный анализ периодической последовательности радиоимпульса
Воспользуемся тем же соотношением (19) и (11), но для периодической последовательности:
 (20)
(20)
Получим: 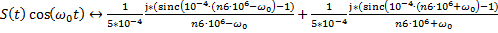 (21)
(21)
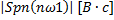

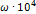 рад/с
рад/с
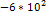

Рис. 8. Амплитудный спектр периодической последовательности радиоимпульсов
Проанализировав, полученные данные можно сделать выводы, что спектр последовательности радиоимпульсов представляет собой спектр периодического импульса, но «раздвоенного» и перенесенного в область высоких частот ± 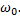 Спектр периодической последовательности радиоимпульсов дискретен.
Спектр периодической последовательности радиоимпульсов дискретен.
Раздел 5
|
|
|


