Перестановки, размещения и сочетания

Лекция. Элементы комбинаторики

 

Учебные вопросы лекции

 

1. Правила суммы и произведения

2. Перестановки, размещения и сочетания

3. Бином Ньютона и свойства биномиальных коэффициентов

 

Содержание лекции

Вступительная часть

 

Комбинаторика – один из разделов дискретной математики, который приобрел большое значение в связи с его использованием в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике. Большинство задач комбинаторики можно сформулировать как задачи конечных множеств.

Среди бинарных отношений, заданных на том или ином множестве объектов, важную роль играют отношения порядка.

Напомним, что упорядочением множества Х (или порядком на Х) называется рефлексивное (х £ х), антисимметричное (если х £ y и y £ х, то х = y) и транзитивное (если х £ y и y £ z, то х £ z) отношение. При х £ y и х ¹ y пишут х < y (отношение строгого порядка).

Пара элементов (х, y) Î X² может и не находиться в отношении ρ = £. Если, однако, х £ y или y £ х для каждой пары (х, y), то множество Х называется линейно упорядоченным множеством (или цепью). В общем же случае говорят о частичном порядке на Х или о частично упорядоченном множестве.

Примерами линейно упорядоченных множеств могут служить множество натуральных чисел, множество всех точек прямой в их естественной упорядоченности, конечный отрезок натурального ряда и т.д.

Одной из задач комбинаторики является определение количества различных подмножеств из заданного конечного множества Х = {х₁, х₂, …, х_n}, которые можно образовать выборкой элементов из Х по определенным правилам, причем в этих выборках порядок расположения элементов может играть важную роль, а может не играть никакой роли; элементы, входящие в выборку могут повторяться, а могут не повторятся; в выборке могут участвовать все элементы множества Х или не все.

Выборка называется упорядоченной, если порядок следования элементов в ней задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными. Если порядок следования элементов не является существенным, то выборка называется неупорядоченной.

 

Правила суммы и произведения

Решение большинства комбинаторных задач основано на двух простых правилах, которые называются правилами суммы и произведения. Правило суммы позволяет найти число элементов в объединении двух конечных множеств, а правило произведения – число элементов их декартова произведения.

Пусть заданы два непустых конечных множества Х и Y, причем мощности (т.е. количества элементов) этих множеств равны соответственно |X| = k, |Y| = l. Тогда, если X ∩Y = Ø, то

|X UY| = |X| + |Y| = k + l.

Если же X ∩Y = Ø, то |X UY| = |X| + |Y| - |X ∩Y|.

Итак, имеем следующее правило суммы.

Правило суммы. Мощность объединения двух конечных множеств равно сумме мощностей каждого из них, уменьшенной на мощность пересечения этих множеств.

Это правило часто интерпретируют следующим образом: если объект х ÎX можно выбрать k способами и после каждого такого выбора объект yÎY можно выбрать l способами, то выбор либо объекта х, либо объекта y можно осуществлять k + l способами. Здесь следует следить за тем, чтобы ни один из способов выбора объекта х не совпал с каким-нибудь способом выбора объекта y. При наличии же таких совпадений результат равен k + l – m, где m – число совпадений.

Правило суммы индукцией можно обобщить на случай любого конечного числа множеств, например, для трех множеств Х, Y, и Z его можно записать так:

|x ∪ y ∪ z| = |x| + |y| + |z| - |x ∩ y| - |x ∩ z| - |y∩ z| + |x ∩ y ∩ z|.

Правило произведения. Если объект хÎX можно выбрать k способами и после каждого из таких выборов объект yÎY в свою очередь можно выбрать l способами, то выбор упорядоченной пары (х, y) можно осуществить k·l способами (выборы х и y независимы).

На самом деле правило произведения есть ни что иное, как определение мощности декартова произведения двух конечных множеств:

|X x Y| = |X| · |Y|.

Индукцией можно доказать, что

|X₁ x X₂ x …x X_n| = |X₁| |X₂| … |X_n|.

Интерпретируя обобщенное правило произведения, можно сказать так: если элемент х₁ÎX₁ можно выбрать n₁ способами, после каждого выбора этого элемента следующий за ним элемент х₂ÎX₂ можно выбрать n₂ способами, и т.д., после выбора элементов х₁, х₂, …, х_k-1 элемент х_kÎX_k можно выбрать n_k способами, то кортеж (х₁, х₂, …, х_k) можно выбрать n₁∙ n₂∙… ∙n_k способами.

Заметим, что некоторые из заданных множеств или даже все множества могут совпадать между собой.

 

Перестановки, размещения и сочетания

Начнем с определения размещений.

Пусть дано множество Х={х₁, х₂, …, х_n}. Сколько кортежей длины k можно составить из элементов этого множества, если все элементы каждого кортежа различны?

1. Размещения без повторений. Кортежи, подчиненные этому условию, называются размещениями без повторений из n элементов по k; их число обозначают символом .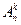

Вычислим . На первое место у нас имеется n кандидатов (каждый из n элементов данного множества). После того, как первое место заполнено, на второе место остаются n -1 кандидатов, на третье - n – 2 кандидатов и т.д. На k-ое место имеется n – k +1 кандидатов (после того, как мы выберем k – 1 элемент, останется n – (k - 1) = n – k + 1 элементов). Применяя правило произведения, находим

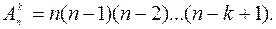(1)

Эту формулу можно записать иначе, умножив числитель и знаменатель на (n – k) (n – k – 1)…1:

 

(2)

2. Перестановки без повторений. Два размещения без повторений из n элементов по n состоят из одних и тех же элементов, расположенных в различном порядке. Поэтому такие размещения называются перестановками из n элементов без повторений. Их число обозначается символом P_n. По формуле (2) или (1) получаем

. (3)

По определению считается, что 0! = 1! = 1.

3. Размещения с повторениями. Множества х₁, х₂, …, х_k, из которых составляются выборки (кортежи), могут иметь общие элементы. В частности, все они могут совпадать с одним и тем же множеством Х, содержащим n элементов. Кортежи длины k, составленные из элементов множества Х = {х₁, х₂, …, х_n}, называются размещениями с повторениями из n элементов по k; их число обозначается символом . Из правила произведения сразу вытекает, что

(4)

4. Перестановки с повторениями. Пусть дан кортеж длины n, составленный из элементов множества Х = {х₁, х₂, …, х_k}, причем элемент х₁ входит в этот кортеж n₁ раз, …, элемент х_k – n_k раз. Если переставлять в этом кортеже элементы, будут получаться новые кортежи, имеющие тот же состав, т.е. такие, что элемент х₁ входит в них n₁ раз,…, элемент х_k – n_k раз. Такие кортежи называются перестановками с повторениями из элементов х₁, х₂, …, х_k, имеющими состав (n₁, n₂, …, n_k). Число таких перестановок обозначается символом Р(n₁, n₂, …, n_k).

С помощью правила произведения находим, что число перемещений элементов, не меняющих данную перестановку, равно n₁! n₂!…n_k! Но n чисел можно переставлять друг с другом n! способами. Поэтому число различных перестановок элементов, имеющих состав (n₁, n₂, …, n_k), т.е. Р(n₁, n₂, …, n_k), в n₁! n₂!…n_k! раз меньше, чем n!:

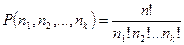, (5)

где n₁+ n₂+ …+ n_k = n.

Пример 1. Сколько различных кортежей получится, если переставлять буквы в слове '' математика ''. Это слово имеет состав (2, 3, 2, 1, 1, 1) и поэтому получается

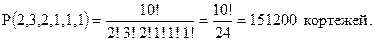
5. Сочетания без повторений. Рассмотрим следующую задачу комбинаторики: сколько подмножеств, содержащих по k элементов каждое, можно составить из элементов данного конечного множества Х = {х₁, …, х_n}. Такие подмножества называются сочетаниями без повторений из n элементов по k, а их число обозначается символом . Выведем формулу, вычисляющую .

Возьмем какое-нибудь подмножество A Ì Х, содержащие k элементов. Это подмножество можно упорядочить k! способами, при этом каждое такое подмножество может быть получено таким образом. Значит число упорядоченных k-элементных подмножеств, составленных из элементов множества Х, в k! раз больше числа неупорядоченных k-элементных подмножеств в Х. Но число упорядоченных k-элементных подмножеств равно , а число всех k-элементных подмножеств мы обозначили через , поэтому = k! , откуда

. (6)

Сочетания без повторений имеют много приложений в различных областях и, в первую очередь, в теории вероятностей, в теории кодирования информации и др.

Рассмотрим два важных свойства сочетаний без повторений.

1⁰. , если 0 £ k £ n.

Действительно, .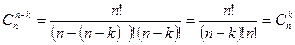

2⁰. при 0 £ k £ n.

В самом деле:

= .

6. Сочетания с повторениями. Сочетаниями из n элементов по k элементов с повторениями называются группы (выборки), содержащие k элементов, причем каждый элемент принадлежит к одному из n типов.

Например, из трех элементов x, y, z можно составить такие сочетания по два с повторениями:

xx, xz, yz, xy, yy, zz.

Число различных сочетаний из n элементов по k с повторениями обозначается символом и вычисляется по формуле

. (7)

Действительно, каждое сочетание полностью определяется, если указать, сколько элементов каждого из n типов в него входит. Поставим в соответствие каждому сочетанию последовательность нулей и единиц, составленному по такому правилу: напишем подряд столько единиц, сколько элементов первого типа в сочетание, далее поставим нуль и после него напишем столько единиц, сколько элементов второго типа содержит это сочетание и т.д. Например, написанным выше сочетаниям из трех букв по две будут соответствовать такие последовательности:

1100, 1001, 0101, 1010, 0110, 0011.

Таким образом, каждому сочетанию из n элементов по k соответствует последовательность из k единиц и n –1 нулей, и наоборот, по каждой такой последовательности однозначно восстанавливается такое сочетание. Поэтому число сочетаний из n элементов по k с повторениями равно числу последовательностей из k единиц и n –1 нулей, т.е. равно .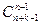

Пример 2. Кости домино можно рассматривать как сочетания с повторениями по два из семи цифр 0, 1, 2, 3, 4, 5, 6. Тогда

.

3. Бином Ньютона и свойства биномиальных коэффициентов

Как известно, (a + b)² = a² + 2ab + b², (a + b)³ = a³ + 3a²b + 3ab² + b³. Возникает вопрос: как раскрыть скобки при вычислении выражения (а + b)ⁿ? Ответ на этот вопрос дает следующая

Теорема. Имеет место равенство

(8)

или

.

Доказательство. Перемножим последовательно а + b на себя n раз. Тогда получим сумму 2ⁿ слагаемых вида d₁d₂…d_n, где d_i (i = 1, 2, …, n) равно либо а, либо b. Разобъем все слагаемые на n + 1 групп В₀, В₁,…, В_n, отнеся к В_k все те произведения, в которых b встречается множителем k раз, а a – (n – k) раз. Число произведений в В_k равно , а каждое слагаемое в В_k равно а^n-k b^k, поэтому

,

что и требовалось доказать.

Доказанную теорему называют биномиальной теоремой, а числа - биномиальными коэффициентами. Равенство (8) часто называют биномом Ньютона, хотя исторически эту формулу знали еще в XI в. (Омар Хайям), в XVII в. (Б. Паскаль) и др. Заслуга Ньютона в этом вопросе состоит в том, что он обобщил формулу (8) для дробного показателя n.

Справедлива следующая обобщенная полиномиальная теорема:

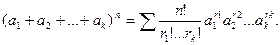
r₁ ³ 0,..., r_k ³ 0,

r₁ + r₂ + … + r_k = n,

где суммирование проводится по всем неотрицательным значениям r_i (i=1, 2,…, k).

Доказательство полиномиальной теоремы проводится по аналогии с формулой бинома Ньютона (предлагаем его провести самостоятельно).

Непосредственным вычислением или другими простыми соображениями легко доказывается следующие соотношения:

1⁰. (в (8) достаточно положить a = b = 1).

2⁰. (в (8) положить а = 1, b = -1).

3⁰.

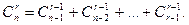
4⁰.

При решении комбинаторных задач используется ряд широко распространенных методов, среди которых следует особо отметить метод включений и исключений, метод производящих функций и метод рекуррентных соотношений, которые важны и сами по себе, так как находят применение не только в комбинаторике, но и во многих разделах математики и ее приложений. Рассмотрим некоторые из этих методов.

Поделиться:

Воспользуйтесь поиском по сайту: