 |
Задачи для самостоятельного решения.
|
|
|
|
Элементы комбинаторики.
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненным тем или иным условиям, можно составить из элементов принадлежащих заданному множеству.
Основные правила комбинаторики.
1. Правило суммы.
Если некоторый объект А1 можно выбрать n1 способами, а объект А2 – другими n2 способами и т.д., объект Аk - – nk способами, отличными от предыдущих, то выбор одного из объектов А1 или А2, или… т.д., или Аk можно произвести n1 + n2 +.. + nk способами.
Пример 1. Пусть в корзине имеется 7 апельсинов, 5 бананов, и 10 яблок. Сколькими способами можно выбрать один фрукт из корзины?
Решение. Т.к. есть 7 способов выбрать апельсин, 5 способов выбрать банан, и 10 способов выбрать яблоко, то всего имеется 7+5+10=22 способа выбрать один фрукт из корзины.
2. Правило произведения.
Если объект А1 можно выбрать n1 способами, а после каждого такого выбора другой объект А2 можно выбрать n2 способами (независимо от выбора А1) и т.д., наконец, после выбора объекта Ак-1 объект Ак можно выбрать nк способами, то одновременный выбор объектов А1, А2, …,Ак в указанном порядке можно осуществить n1∙n2∙…∙nк способами.
Пример 2. Определить, сколько двузначных чисел можно записать в десятичной системе счисления.
Решение. Число десятков двузначного числа может принимать одно из девяти значений: 1, 2, 3, 4, 5, 6, 7, 8, 9. Число единиц может принимать одно из десяти значений: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего получим  двузначных чисел.
двузначных чисел.
Перестановки.
Перестановки – это комбинации, состоящие из одних и тех же n различных элементов и отличающиеся друг от друга только их порядком.
Число перестановок из n элементов обозначается  и
и 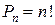
|
|
|
Пример 3. Сколькими способами можно расставить 5 книг на полке?
Решение. P5 =5!=1∙2∙3∙4∙5=120.
Если среди n элементов есть n 1 элементов одного вида, n 2 элементов другого вида и т.д., то число перестановок с повторениями определяется формулой

Пример 4. Сколько различных слов можно составить из букв слова «экономика»?
Решение. Всего в рассматриваемом слове 9 букв. При этом повторяются буквы «о» (2 раза), «к» (2 раза). Следовательно, 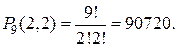
----------------------------------------------------------------------------------------------------------------
Комбинаторика. Стр.1
Размещения.
Размещения – это комбинации, составленные из n различных элементов по m, которые отличаются либо составом элементов, либо их порядком.
Число размещений из n элементов по m обозначается  и
и 
Число размещений из n элементов по m с повторениями равно 
Пример 5. Сколько размещений можно получить из букв «б», «а», «р», взятых по две, если: а) буквы в наборе не повторяются; б) буквы могут повторяться?
Решение. а)  ; б)
; б) 
Сочетания.
Сочетания – это комбинации из n элементов по m, которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m обозначается  и
и 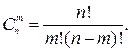
Число сочетаний с повторениями из n элементов по m равно числу сочетаний без повторений из n + т –1 элементов по т элементов, т.е.  .
.
Пример 6. В продаже имеются гвоздики, розы, гладиолусы, ирисы, тюльпаны, астры и васильки. Сколькими способами можно составить букет из пяти цветков, если: а) цветы в букете все различные; б) цветы в букете могут повторяться?
Решение. а) 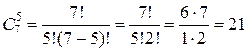 ;
;
б) 
Число перестановок, размещений и сочетаний связаны по формуле:  .
.
Задачи для самостоятельного решения.
№1. Сколькими способами можно составить трёхзначное число, делящееся на пять?
№2. В чемпионате участвуют 12 команд. Сколькими различными способами могут быть распределены три различные медали?
|
|
|
№3. Имеется 7 путёвок в различные дома отдыха и 7 кандидатов. Сколькими способами можно распределить эти путёвки?
№4. В классе 22 учащихся. Двух из них следует назначить дежурными. Сколькими способами это можно сделать?
№5. Сколькими способами можно посадить за круглый стол 7 мужчин и 7 женщин так, чтобы никакие две женщины не сидели рядом?
№6. В колоде 52 карты. Раздаются 3 карты. Сколько может быть случаев появления одного туза среди розданных карт?
----------------------------------------------------------------------------------------------------------------
Комбинаторика. Стр.2
№7. Какое количество различных символов можно передать не более чем пятью знаками кода Морзе, использующего точку и тире?
№8. Сколько различных диагоналей можно провести в восьмиугольнике? стоугольнике?
№9. Студент сдал два экзамена, получив за них различные положительные оценки. Сколько видов результативных оценок он мог получить?
№10. В группе 25 человек. Сколькими способами можно выстроить их в одну шеренгу? Сколькими способами можно выстроить их в одну шеренгу так, чтобы Иванов и Петров не стояли рядом?
№11. Сколько трёхзначных чисел начинается с 3 или 4?
№12. Сколькими способами можно выбрать 6 различных пирожных в кондитерской, где имеется 11 сортов пирожных?
Домашнее задание.
№1. Автомобильные номера состоят из трех букв и четырёх цифр. Найти число таких номеров, если используется 32 буквы алфавита.
№2. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материя 5 цветов?
№3. В ящике имеется 15 деталей, среди которых 5 бракованных. Сборщик наудачу берёт 3 детали. Сколько будет случаев, когда среди извлеченных трёх деталей будут:
а) все стандартные; б) две стандартные; в) все бракованные?
№4. Сколько машинных слов можно составить из букв слова ВОДОРОД?
----------------------------------------------------------------------------------------------------------------
Комбинаторика. Стр.3
|
|
|


