Схема решения комбинаторных задач.

Основные правила комбинаторики

Правило сложения

Пример. Пусть из пункта А в пункт В можно добраться самолетом, поездом и автобусом, причем между этими пунктами существует 2 авиамаршрута, 1 – железнодорожный и 3 – автобусных. Следовательно, общее число маршрутов между пунктами А и В равно 2 + 1 + 3 =6.

Таким образом, пусть имеется k попарно непересекающихся множеств A₁, A₂, …, A_k, содержащих n₁, n₂, …, n_k элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно n₁ + n₂ + … + n_k.

Правило сложения: если выбор каждого из объектов а_i (i = 1, 2,…, k) можно выполнить n_i способами, то выбор «или a_i, или a₂,…, или a_k» можно произвести 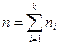способами.

Правило умножения (произведения)

Пример. Сколькими различными способами можно распределить четыре шара по двум лункам, в которые помещается ровно один шар. Очевидно, первую лунку можно заполнить четырьмя способами, так как при выборе первой лунки имеется четыре шара. Вторую лунку можно заполнить тремя шарами, так как после заполнения первой лунки осталось три шара.

Заметим, что с каждым из четырех способов заполнения первой лунки может совпасть любой из трех способов заполнения второй. Поэтому общее число способов распределения двух лунок равно 4 ∙ 3 = 12.

Таким образом, пусть имеется k множеств A₁, A₂, …, A_k содержащих n₁, n₂, …, n_k элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а₁, а₂,..., а_k), где а_i Î А_i (i = 1, 2, …, k), равно n₁ ×n₂ ×…×n_k.

Замечание: под кортежем понимается конечная последовательность (допускающая повторения) элементов какого-нибудь множества.

Запишем теперь правило умножения в общем виде.

Если выбор каждого из k объектов a_i (i = 1, 2,..., k) можно осуществить n_i способами, то выбор «и a₁, и a₂,…, и a_k» можно произвести 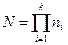способами.

Размещения (перемещения)

Размещениями из n различных элементов по k элементов (0£ k £ n) называются комбинации, составленные из данных n элементов по k элементов, которые отличаются либо самими элементами, либо порядком элементов.

Другими словами, размещением из n различных элементов по k элементов (0£ k £ n) называется упорядоченное подмножество, содержащее k различных элементов данного множества. Все эти подмножества отличаются друг от друга или составом элементов, или порядком их распределения. Но число элементов во всех этих подмножествах равно k.

Выделяют размещения без повторений и размещения с повторениями (элементы могут повторяться).

Например, из трех элементов a, b, c можно составить по два элемента следующие размещения:

без повторений: ab, ac, bc, ba, ca, cb.
с повторениями: aa, ab, ac, bb, bc, ba, cc, ca, cb.
Для определения числа размещений без повторений из n элементов по k учтем, что первый элемент подмножества может быть взят n различными способами, второй – (n – 1) способом,…, k-ый элемент – (n – (k – 1)) способами. Отсюда, используя правило умножения, получаем

, т.е.

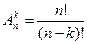
Здесь: n! = 1 ∙ 2 ∙ 3 ∙ … ∙ (n – 1)n, (n – k)! = 1 ∙ 2 ∙ 3 ∙... ∙ (n – k).
Условимся считать 0! = 1, поэтому .

Число размещений с повторениями вычисляется следующим образом: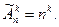

Обратимся к рассмотренному ранее примеру. Вычислим с помощью формул сколько можно составить размещений из имеющихся трех букв по две.
без повторений: 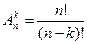. Имеем, 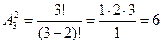(ab, ac, bc, ba, ca, cb).
с повторениями: 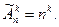Имеем, 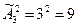(aa, ab, ac, bb, bc, ba, cc, ca, cb).

Пример. В соревнованиях принимают участие 16 команд. Сколькими способами могут распределиться три первых места, т.е. необходимо найти число всех подмножеств, состоящих из трех элементов, отличающихся составом (номерами команд) или порядком их размещения (подмножества № 1, № 2, № 3 и № 2, № 1, № 3 являются разными). Таким образом, имеем дело с размещением без повторений. Тогда искомое число равно

.

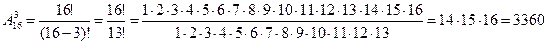Перестановки

Перестановками из n различных элементов называются размещения из этих n элементов по n. Так как каждая перестановка содержит все n элементов множества, то различные перестановки отличаются друг от друга только порядком следования элементов.

Рассматривают перестановки без повторений (n различных элементов) и перестановки с повторениями (k различных элементов, где элементы могут повторяться m₁, m₂, …, m_k раз и m₁ + m₂ + … + m_k = n, где n - общее количество элементов).

Например, из трех элементов a, b, c можно составить следующие перестановки:
без повторений: abc, acb, bca, bac, cab, cba.
с повторениями (буква a повторяется два раза): aabc, aacb, abca, aacb, acab,
acba, baac, baca, bcaa, caab, caba, cbaa.
Задание: составьте из имеющихся элементов перестановки с повторениями, так, чтобы дважды повторялись буквы a и b.

Число всех возможных перестановок из n элементов обозначают P_n.

Перестановки можно считать частным случаем размещений при k = n.

Число всех перестановок без повторений из n элементов вычисляется по формуле: 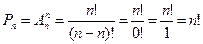, то есть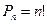

Перестановки c повторениями (k различных элементов, где элементы могут повторяться m₁, m₂, …, m_k раз и m₁ + m₂ + … + m_k = n, где n - общее количество элементов): .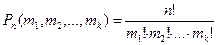

Пример. В условиях предыдущего примера, имеем,

без повторений: 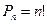(abc, acb, bca, bac, cab, cba).
с повторениями (буква a повторяется два раза): 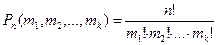В данном случае m₁=2 (буква a повторяется дважды), m₂=1 (буква b повторяется один раз), m₃=1 (буква с повторяется один раз). Следовательно, n=2+1+1=4. Учитывая условие задачи, формула приобретает вид 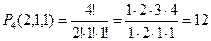(aabc, aacb, abca, aacb, acab, acba, baac, baca, bcaa, caab, caba, cbaa).
с повторениями (буквы а и b повторяются дважды): 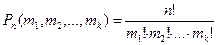В данном случае m₁=2 (буква a повторяется дважды), m₂=2 (буква b повторяется дважды), m₃=1 (буква с повторяется один раз). Следовательно, n=2+2+1=5. Учитывая условие задачи, формула приобретает вид 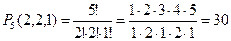(baabc, ababc, aabbc, aabcb, babac, abbac, abacb, babca, abbca, abcba, abcab, baacb, aacbb, bacab, acbab, acabb, bacba, acbba, bbacc, bbaca, bbcaa, bcbaa, bcaab, cbaab, cabab, caabb, bcaba, cbaba, cabba, cbbaa).
Пример. Сколькими способами можно расставить 6 различных книг на одной полке?
Решение. Имеем дело с перестановками без повторений. Искомое число способов равно Р₆ = 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 =720.
Действительно, первую книгу можно выбрать шестью способами, вторую – пятью способами и т. д., последнюю – одним способом. По правилу умножения общее число способов равно 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 =720.

Сочетания

Пусть дано множество, состоящее из n элементов. Сочетанием из n элементов по k (0 £ k £ n) элементов называется любое подмножество, которое содержит k различных элементов данного множества. Таким образом, различными подмножествами считаются только те, которые отличаются составом элементов. Подмножества, отличающиеся друг от друга лишь порядком следования элементов, не считаются различными.

Другими словами, с очетаниями из n различных элементов по k элементов называются комбинации, составленные из данных n элементов по k элементов, которые отличаются хотя бы одним элементом.Отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов.

Число всех возможных сочетаний без повторений из n элементов по k обозначается .

Так как число перестановок из k равно k!, то число размещений из n элементов по k будет в k! раз больше, чем число сочетаний из n элементов по k, т.е. 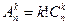, отсюда .

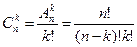Сочетания c повторениями (n элементов, взятых по k, где элементы в наборе могут повторяться): .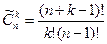

Пример 1. Возьмем газеты: Челябинский рабочий (ЧР), Комсомольскую правду (КП), Аргументы и факты (АиФ). Для практических занятий студентов по литературному редактированию необходимо составить наборы из двух газет. Сколько таких наборов получится, если:
1. газеты в наборе не повторяются?
2. можно брать по две одинаковых газеты?

Решение:
1. Имем дело с сочетаниями без повторений, следовательно, применим формулу , получаем 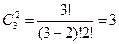. Таким образом, можно составить три набора: 1-ый – ЧР и КП (ЧР, КП и КП, ЧР – один и тот же набор), 2-ой – ЧР и АиФ, 3-ий – КП и АиФ.

2. Имем дело с сочетаниями с повторениями, следовательно, применим формулу 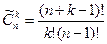, получаем 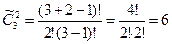. Таким образом, можно составить шесть наборов: 1-ый – ЧР и КП, 2-ой – ЧР и АиФ, 3-ий – КП и АиФ, 4-ый – ЧР и ЧР, 5-ый – КП и КП, 6-ой – АиФ и АиФ.

Пример 2. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение. Так как порядок выбранных четырех человек не имеет значения и люди повторяться не могут, то это можно сделать способами (применили формулу числа сочетаний без повторений).

Пример, показывающий применение формул комбинаторики к нахождению вероятности события.

Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?

Решение. Пусть М – событие, вероятность которого надо найти. Число n – число всех элементарных событий – равно числу размещений из 10 по 2, т. е. n = 10!/ (10 – 2)! Число m – число элементарных событий, благоприятствующих собы­тию М – равно 1. Поэтому, используя определение вероятности (Р(А) = m /n), получаем: Р(М) = 1/90

Схема решения комбинаторных задач.

КОМБИНАТОРНАЯ ЗАДАЧА

 

входят все элементы входит часть элементов

 

порядок элементов

 

имеет значение не имеет значения

 

перестановки размещения сочетания

P_n=n!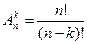

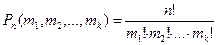
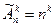
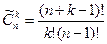
СПИСОК ЛИТЕРАТУРЫ

1. Грес П.В. Математика для гуманитариев: Уч. пособие / П.В. Грес. – М.: Юрайт, 2000. – 112 с.

2. Баврин И.И., Матросов В.Л. Высшая математика: Учеб. для студ. Высш. учеб. заведений. – М.: Гуманит. Изд. Центр ВЛАДОС, 2002. – 400 с.: ил.

3. Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. – М.: Айрис-пресс, 2004. – 256 с. – (Высшее образование).

4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Уч. пособие / В.Е. Гмурман. – М.: Высш. шк., 2002. – 405 с.

5. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие / В.Е. Гмурман – М.: Высш. шк., 2003. – 497 с.

6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – 6-е изд. – М.: Наука. Главная редакция физико-математической литературы, 1986. – 576 с.

 

Семинарское занятие № 3, № 4

Комбинаторика

Выполнить решение следующих задач:

1. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

Решение: по правилу умножения двух девушек можно выбрать 14*13=182 способами, а двух юношей 6*5=30 способами. Т.к. следует выбрать двух студенток или двух юношей, то по правилу сложения 182+30=212 способов.

 

2. Составить различные размещения по 2 из элементов множества 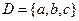; подсчитать их число.

Решение: .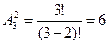

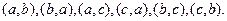
3. Составить различные перестановки из элементов множества 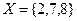; подсчитать их число.

Решение: 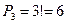. (2,7,8), (2,8,7), (7,2,8), (7,8,2), (8,2,7), (8,7,2).

4. Сколькими способами можно расставить на полке 7 различных книг?

Решение: .

5. Составить различные сочетания по 2 из элементов множества 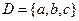; подсчитать их число.

Решение: .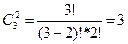

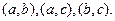
6. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики?

Решение: т.к. порядок выбора цветов не имеет значения, то .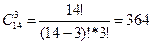

7. Из 4 первокурсников, 5 второкурсников 6 третьекурсников надо выбрать 3 студента на конференцию. Сколькими способами можно осуществить этот выбор?

Решение: т.к. порядок выбора студентов не имеет значения, то .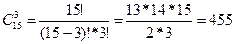

Упражнения для контроля:

Поделиться:

Воспользуйтесь поиском по сайту: