Общие теоретические сведения

Раздел 6. Методы решения комбинаторных задач как средство обработки и интерпретации информации

Цель занятия: научиться определять виды комбинаций, находить их количество, вероятность наступления события.

Вопросы для обсуждения

1. Понятие комбинаторной задачи.

2. Основные формулы комбинаторики.

3. Решение комбинаторных задач, соответствующих специфике профессиональной деятельности.

4. Виды событий. Определение вероятности случайного события.

Задания и вопросы для подготовки к занятию

1. Даны буквы: A, B, C, D, E. Составьте различные комбинации из них по три буквы. Сколько комбинаций получится, если: а) буквы не повторяются; б) буквы могут повторяться; в) комбинация букв обозначает название треугольника?

2. Подбросьте монетку 5 раз. Запишите результаты бросков. Сколько «орлов» и «решек» получилось в Вашем опыте? Сравните с результатами других студентов. Сколько различных комбинаций «орлов» и «решек» возможно? Какова вероятность, что у кого-нибудь из группы будет ваша комбинация?

Общие теоретические сведения

Решение комбинаторных задач связано с выбором из некоторого множества подмножеств, обладающих определенными свойствами, и упорядочением множеств. Область математики, которая исследует решение комбинаторных задач, называется комбинаторикой. Все задачи, рассматриваемые комбинаторикой, требуют ответа на вопрос «сколько?» или «сколькими способами?».

Правило суммы. Если элемент a из одного множества можно выбрать m способами, а элемент b из другого множества – k способами, то выбор «либо a, либо b» можно осуществить m + k способами, при условии, что данные множества не пересекаются.

Задача 1. На столе лежат 3 яблока и 4 груши. Сколькими способами можно выбрать один фрукт?

Решение. В данной задаче речь идет о выборе одного элемента из двух непересекающихся множеств. Можно выбрать яблоко или грушу, поэтому выбираем правило суммы. Яблоко можно выбрать 3 способами, грушу – 4. Таким образом, общее число способов: 3 + 4 = 7.

Ответ: 7.

Правило произведения. Если элемент a из одного множества можно выбрать m способами, а элемент b из другого множества – k способами, то выбор пары «a и b» можно осуществить m ∙ k способами.

Задача 2. В пенале лежат 5 ручек и 4 карандаша. Сколькими способами можно выбрать пару, состоящую из ручки и карандаша?

Решение. 1 способ (метод перебора).

Пронумеруем ручки и карандаши. Составим таблицу всех возможных вариантов пар, которые можно составить из карандаша и ручки:

	ручки
карандаши
	(1;1)	(1; 2)	(1; 3)	(1; 4)	(1; 5)
	(2; 1)	(2; 2)	(2; 3)	(2; 4)	(2; 5)
	(3; 1)	(3; 2)	(3; 3)	(3; 4)	(3; 5)
	(4; 1)	(4; 2)	(4; 3)	(4; 4)	(4; 5)

Подсчитаем их количество: 4 строки умножим на 5 столбцов, получим 20 пар. То есть пару, состоящую из карандаша и ручки, можно выбрать 20 способами.

2 способ (правило произведения).В задаче речь идет о двух множествах, выбрать надо карандаш и ручку. Применим правило произведения. Карандаш можно выбрать 4 способами, а ручку – 5. Таким образом, общее число способов: 4 ∙ 5 = 20.

Ответ: 20.

Задача 3. Сколько существует двузначных чисел?

Решение. Двузначное число состоит из двух цифр: . Первая цифра – число десятков (множество А), вторая – число единиц (множество В):

А = {1, 2, 3, 4, 5, 6, 7, 8, 9}, B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Задачу можно переформулировать: сколькими способами из элементов множеств A и B можно составить пару упорядоченных элементов?

Согласно правилу произведения: 9 ∙ 10= 90.

Ответ: 90.

Перестановка без повторенийиз n элементов

Дано множество, состоящее из n различных элементов.

Перестановкой называется упорядоченное множество, составленное из данных элементов.

Например, для множества { a, b, c } существуют следующие варианты перестановок, которые можно найти с помощью метода перебора:

{ a, b, c }, { a, c, b }, { b, a, c }, { b, c, a }, { c, a, b }, { c, b, a }.

Число всевозможных перестановок из n элементов обозначается P_n и находится по формуле

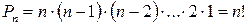(1)

Число n! читается как «n факториал». Считается, что 1! = 1, 0! = 1.

Например, P ₃ = 3!= 1∙2∙3=6.

Перестановка с повторениямииз n элементов

Дано множество, состоящее из n элементов из которых k и т элементов повторяются. При этом от перестановки одинаковых элементов вид упорядоченного множества не меняется.

Например, для множества { a, а, c } существуют следующие варианты перестановок, которые можно найти с помощью метода перебора:

{ a, а, c }, { a, c, а }, { c, a, а }.

Число всевозможных перестановок из n элементов с k и т повторениями обозначается P_{n; k , т} и находится по формуле

(2)

Например, ; .

Размещение без повторений из n элементов по k элементам

Дано множество, состоящее из n элементов.

Размещением без повторений из n элементов по k называется перестановка из k элементов, выбранных из n -элементного множества один раз.

Например, для множества { a, b, c } существуют следующие варианты размещений без повторений по 2 элементам, которые можно найти с помощью метода перебора: { a, b }, { a, c }, { b, a }, { b, c }, { c, a }, { c, b }.

Число всевозможных размещений без повторений k из n элементов обозначается и находится по формуле

(3) или . (4)

Например, или ;

или .

Размещение с повторениями из n элементов по k элементам

Дано множество, состоящее из n элементов.

Размещением c повторениями из n элементов по k называется перестановка из k элементов, выбранных из n -элементного множества, причем каждый элемент может быть выбран несколько раз.

Например, для множества { a, b, c } существуют следующие варианты размещений с повторениями по 2 элементам, которые можно найти с помощью метода перебора: { a, b }, { a, c }, { b, a }, { b, c }, { c, a }, { c, b }, { a, a }, { b, b }, { c, c }.

Число всевозможных размещений с повторениями k из n элементов обозначается и находится по формуле

. (5)

Например, .

Сочетание без повторений из n элементов по k элементам

Дано множество, состоящее из n элементов.

Сочетанием без повторений из n элементов по k элементам называется неупорядоченное подмножество данного множества, состоящее из k элементов.

Например, для множества { a, b, c } существуют следующие варианты сочетаний без повторений по 2 элементам, которые можно найти с помощью метода перебора: { a, b }, { a, c }, { c, b }.

Число всевозможных сочетаний без повторения k из n элементов обозначается и находится по формуле

(6)

Например, или ;

или .

Сочетание с повторениями из n элементов по k элементам

Дано множество, состоящее из n элементов.

Сочетанием с повторениями из n элементов по k называется неупорядоченное подмножество данного множества, состоящее из k элементов, причем элементы могут повторяться.

Например, для множества { a, b, c } существуют следующие варианты сочетаний с повторениями по 2 элементам, которые можно найти с помощью метода перебора: { a, b }, { a, c }, { c, b }, { a, a }, { b, b }, { c, c }.

Число всевозможных сочетаний с повторениями k из п элементов обозначается и находится по формуле:

. (7)

Например, .

При решении задач в первую очередь необходимо определить, является ли эта задача комбинаторной, т. е. можно ли сформулировать задачу в форме вопроса «сколькими способами?». Затем необходимо определить, какое правило надо применить для решения задачи.

Важно определить, о скольких множествах идет речь:

a) если два и более непересекающихся множества, то возможны два варианта:

− если элементы множеств связаны с помощью союза «или» (выбирается один элемент), тогда применяется правило суммы;

− если элементы множеств связаны с помощью союза «и» (выбирается группа), тогда применяется правило произведения;

б) если одно множество, то для определения формулы можно обратиться к таблице 1. Для этого важно определить: сколько элементов множества участвуют, важен ли порядок и разрешены ли повторы.

Таблица 1

Количество элементов множества	Порядок	Повторы	Название	Формула
Все элементы	Порядок существенен	Повторы отсутствуют	Перестановка без повторенийиз n элементов
Все элементы	Порядок существенен	Повторы разрешены	Перестановка с k и т повторяющимися элементами из n элементов
Не все элементы множества	Порядок существенен	Повторы отсутствуют	Размещение без повторений из n элементов по k элементам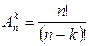
Не все элементы множества	Порядок существенен	Повторы разрешены	Размещение с повторениями из n элементов по k элементам
Не все элементы множества	Порядок не существенен	Повторы отсутствуют	Сочетание без повторений из n элементов по k элементам
Не все элементы множества	Порядок не существенен	Повторы разрешены	Сочетание с повторениями из n элементов по k элементам

 

Теория вероятностей – раздел математики, в котором изучаются закономерности, присущие массовым случайным явлениям.

Случайное событие – исход наблюдения, эксперимента или опыта, который при реализации некоторого комплекса условий может произойти, а может и не произойти.

Элементарный исход – один из возможных вариантов результата опыта.

Равновозможные исходы – элементарные исходы, которые имеют одинаковый шанс произойти или не произойти.

Несовместные исходы – исходы, которые одновременно произойти не могут.

Событие называют достоверным, если оно непременно должно произойти. Событие называют невозможным, если оно заведомо не наступит.

Событием, противоположным некоторому событию А, называют событие 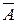, состоящее в том, что А не наступило.

События А и В называются несовместными, если наступление одного из них исключает возможность наступления другого.

Говорят, что событие В следует из события А, если событие В происходит всегда, когда произошло событие А. Два события А и В называются равными, если из А следует В и из В следует А.

События называются независимыми, если появление одного события не влечет появление другого.

Суммой (объединением) двух событий А и В называется событие А + В, состоящее в том, что произошло событие А или событие В.

Произведением (пересечением) двух событий А и В называется событие АВ, заключающееся в совместном наступлении событий А и В.

Классическое определение вероятности. Пусть некоторый опыт имеет n равновозможных и несовместных исходов. Вероятностью Р (А) события А называется отношение числа благоприятных исходов m (А) к общему числу n несовместных равновозможных исходов:

. (8)

Свойства вероятности

1. Для любого случайного события .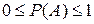

2. Пусть А ₁, А ₂, …, А_k – все события, которые могут произойти в результате опыта. Тогда (9)

3. Пусть А – некоторое событие, – противоположное событие, тогда верно равенство . (10)

Правило суммы вероятностей. Вероятность суммы несовместных событий есть сумма вероятностей этих событий:

. (11)

Правило произведения вероятностей независимых событий. Вероятность произведения событий есть произведение вероятностей этих событий:

. (12)

События А и В называются зависимыми, если появление одного из них изменяет вероятность появления другого.

Условной вероятностью Р (В/А) называется вероятность события В, вычисленная в предположении, что событие А уже произошло.

Правило произведения вероятностей зависимых событий. Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло, т.е.

. (13)

Вероятность суммы совместных событий. Вероятность суммы совместных событий есть сумма вероятностей этих событий без вероятности из совместного наступления:

. (14)

Пусть в результате некоторого случайного испытания может произойти или не произойти определенное событие А. Если событие произошло, испытание называется успешным, а событие – успехом; противоположное событие – неудача. Испытание повторяется n раз. При этом соблюдаются следующие условия: вероятность успеха в каждом испытании одна и та же; вероятность противоположного события (причем ; результат любого испытания не зависит от исходов предыдущих испытаний.

Такая последовательность испытаний с двумя исходами (успех/неудача) называется последовательностью независимых испытаний Бернулли или схемой Бернулли.

Вероятность того, что в схеме Бернулли из n независимых испытаний произошло ровно k успехов, находится по формуле Бернулли:

. (15)

Следствия из формулы Бернулли:

1. , .

2. .

 

 

Рассмотрим задачи на нахождение вероятности события.

Задача 4. Вася, Петя, Коля и Саша бросили жребий – кому начать игру. Найдите вероятность того, что начинать игру должен Коля.

Решение. Случайный эксперимент – бросание жребия. Элементарное событие – участник, который выиграл жребий. Общее число независимых равновозможных элементарных событий п =4. Событию А= {жребий выиграл Коля} благоприятен только один исход, поэтому т= 1. Тогда .

Задача 5. В случайном эксперименте симметричную монету бросили три раза. Какова вероятность того, что орел выпадет ровно два раза?

Решение. В описанном эксперименте элементарные исходы – тройки «орлов» (О) и «решек» (Р). Выпишем их все в таблицу:

Элементарный исход	ООО	ООР	ОРО	ОРР	РОО	РОР	РРО	РРР
Число орлов

Всего исходов 8, из них благоприятных 3, тогда .

Задачу можно решить по формуле вероятности двух успехов в серии из трех испытаний по формуле Бернулли (15): , где р= 0,5 – вероятность «орла» (успеха) при одном броске, q = 0,5 – вероятность «решки» (неудачи).

Ответ: 0,375.

Задача 6. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в одном автомате закончится кофе, равна 0,3; а в обоих автоматах – 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение. Определим события и их вероятность: А = {кофе закончится в первом автомате}, B ={кофе закончится во втором автомате}; и .

Событие С ={кофе останется в обоих автоматах} противоположно событию «кофе закончится хотя бы в одном автомате», т.е. .

По формуле (14) сложения вероятностей найдем вероятность события ; следовательно, .

Ответ: 0,52.

Задача 7. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал, а последние два раза промахнулся.

Решение. Результат каждого следующего выстрела не зависит от предыдущих, поэтому рассматриваются независимые события. Вероятность каждого попадания равна 0,8. Значит, вероятность каждого промаха 1 – 0,8=0,2.

По формуле (12) умножения вероятностей независимых событий находим: .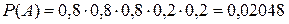

Ответ: 0,02048.

Поделиться:

Воспользуйтесь поиском по сайту: