 |
Задача 7. В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных изделий будет ровно одно окрашенное.
|
|
|
|
Задача 2
В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 5 отличников.
Решение. Задача решается с помощью формулы классической вероятности
Р(А)=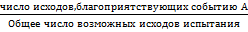 
Общее число элементарных событий n= 
= 
, т.к. всего студентов 12, а надо выбрать 9.
Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию А: среди 9 студентов будет 5 отличников. Очевидно, что число способов, которыми можно выбрать 5 отличников из 8, равно 
Произведем вычисления: 
Тогда используя формулу классической вероятности, получим
Р(А)== 
= 
Ответ: Р(А)= 
Задание №3
На складе имеется 15 холодильников, причем 10 из них изготовлены на Минском заводе. Найти вероятность того, что среди взятых наудачу 5 холодильников окажутся 3 холодильника Минского завода.
Решение.
. Задача решается с помощью формулы классической вероятности
Р(А)=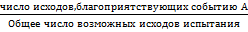
Число элементарных событий выбора 5 холодильников из общего числа 15 n= 
= 
Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию А: среди 5 холодильников будет 3 холодильника Минского завода. Очевидно, что число способов, которыми можно выбрать 3 холодильника Минского завода из 10, равно 
Произведем вычисления: 
0
Р(А)== 
= 
=0,3996 
Ответ: Р(А)=0,4
Задача 4
В лотерее участвуют 10 билетов, 4 из которых выигрывают. У одного из участников на руках 3 билета. Найти вероятность того, что 2 из них выиграют.
Решение. Воспользуемся классической формулой нахождения вероятности наступления события А: Р(А)=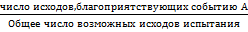
Подсчитаем общее возможных исходов как число сочетаний , т.е.
|
|
|
Число элементарных событий n= = 
Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию А вычислим по формуле, т.е. среди 3 билетов будут 2 выигрышных. Очевидно, что число способов, которыми можно выбрать 2 билета из 3, равно 
роизведем вычисления: 
Р(А)= 
= 
Ответ: Р(А)=3/35
Задача 5.
В партии из 12 деталей имеется 7 стандартных. Наудачу отобраны 5 деталей. Найти вероятность того, что среди отобранных деталей будет ровно 3 стандартных.
Решение.
Задача решается с помощью формулы классической вероятности
Р(А)=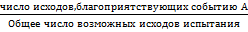
Всего в ящике 12 деталей, выбрать надо 5.
Число элементарных событий выбора 5 деталей из общего числа 12 равно n= = 
Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию А: среди 5 деталей будет 3 стандартных. Очевидно, что число способов, которыми можно выбрать 3 стандартные детали из7, равно 
а число способов, которыми можно довыбрать к ним детали нестандартные равно
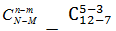
Произведем вычисления: 
0
Р(А)== 
= 
=0,44
Ответ: Р(А)=0,44
Задача 6
В группе, состоящей из 4 женщин и 3 мужчин, разыгрываются 4 билета в театр. Найти вероятность того, что среди обладателей билетов женщин и мужчин будет поровну.
Решение.
Воспользуемся классической формулой нахождения вероятности наступления события А: Р(А)=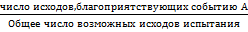
Р(А)=m/n, где m-число исходов, благоприятствующих появлению события А, n- общее число возможных исходов испытания. Общее число возможных исходов (розыгрыш 4 билетов среди 7 человек) равно числу сочетаний 
, т.е.
n= = 
Число исходов, благоприятствующих появлению событию А (билеты в театр получат любые 2 женщины и любые два мужчины) 
.= 
* 
* 
Тогда искомая вероятность интересующего нас события:
Р(А)= 
= 
Ответ. Р(А)=18/35=0,514
Задача 7. В коробке имеется 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди извлеченных изделий будет ровно одно окрашенное.
|
|
|
Решение. Задача решается с помощью классической формулы для вычисления вероятностей:
.
Общее число возможных исходов равно числу сочетаний 
. Число исходов, благоприятствующих появлению m окрашенных изделий, равно . Отсюда вероятность интересующего нас события: 
Число элементарных событий выбора 2 деталей из общего числа 5 равно n= = 
Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию А: среди 2 деталей будет 1 окрашенная. Очевидно, что число способов, которыми можно выбрать 1 изделие из 2, равно 
Произведем вычисления: 
Р(А)= 
= 
Ответ: Р(А)=0,6
8) В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 путевок. Найти вероятность того, что среди обладателей путевок окажутся две девушки.
Решение. Задача решается с помощью формулы классической вероятности
Р(А)=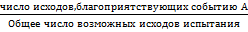
Общее число элементарных событий выбора 5 путевок из общего числа 25 n= = 
Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию А: среди 5обладателей путевок окажутся 2 девушки. Очевидно, что число способов, которыми можно выбрать 2 девушек из 10, равно 
Произведем вычисления: 
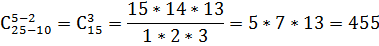
Р(А)= 
= 
= 
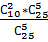=0,3853754 
Ответ: Р(А)=0,39
Задание №9
|
|
|
