 |
Векторный базис на плоскости. Координаты вектора
|
|
|
|
А.Г. Коровин
Методические указания
По выполнению контрольной работы №1
По высшей математике
Для групп заочного отделения
Н.Новгород
УДК 517
ББК 22.1я73
К 68
К 68 Коровин А.Г. Методические указания по выполнению контрольной работы №1 по высшей математике для групп заочного отделения. - Н.Новгород: НКИ, 2000. - 71 с.
Обсуждено и одобрено к изданию на заседании кафедры высшей математике от 21.04.99 г. Протокол № 3.
Настоящее пособие является руководством к решению задач по всем разделам высшей математики, включенным в контрольную работу №1 для студентов заочной формы обучения.
Основное назначение пособия - помочь слушателям заочного отделения в приобретении и углублении навыков решения математических задач.
ББК 22.1я73
Ó Нижегородский коммерческий
институт, 2000
Ó Коровин А.Г., 2000
Глава I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
Векторы
Основные понятия и свойства
Определение 1. Вектор - это отрезок прямой, характеризующийся длиной и направлением.
B C
А D
Обозначения векторов: 
, 
, где первая буква соответствует началу, а вторая концу вектора, либо 
.
Длиной, или модулем вектора , называется длина отрезка АВ и обозначается 
или 
.
Вектор, длина которого равна единице, называется единичным вектором: 
Вектор, начало которого совпадает с его концом, называется нулевым вектором и обозначается 
, 
.
Векторы, имеющие одинаковые направления, называются сонаправленными (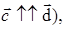
а векторы, имеющие противоположные направления, - противоположно направленными 
.
Векторы называются равными, если они сонаправлены и имеют одинаковые длины.
|
|
|
Векторы называются противоположными, если они имеют равные длины и противоположные направления. Они обозначаются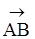 
и 
, 
.
Два ненулевых вектора называются коллинеарными, если они сонаправлены или противоположно направлены.
Векторы называются компланарными, если они лежат в одной плоскости.
Действия над векторами
Сложение векторов осуществляется по двум основным правилам:
- правило параллелограмма;
- правило треугольника.
Правило параллелограмма позволяет найти сумму двух векторов, которые откладываются из одной точки. Результатом сложения является диагональ параллелограмма, выходящая из этой же точки; другая диагональ является разностью этих векторов, т.е.:
|
|
, 
,
|
|
|
, 
,
|
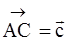то 
, или 
;
|
|
, или 
.
Правило треугольника позволяет найти сумму двух векторов, когда начало одного из них совмещено с концом другого, т. е.
|
В С ес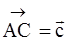ли , , ,
|
, или ;
А
Это правило может быть распространено на сумму любого числа векторов.
Операция сложения векторов обладает следующими свойствами:
1) коммутативность 
2) ассоциативность 
Умножение вектора на число
Определение 2. Произведением ненулевого вектора на число l¹0 называется вектор 
длина которого равна 
, а направление: 
при l>0; 
при l<0.
Умножение вектора на число обладает следующими свойствами:
1) l(b )=(lb) ,
2) l +b =(l+b) ,
3) l +l =l(
).
Теорема 1 Для того, чтобы два вектора и были коллинеарны, необходимо и достаточно, чтобы выполнялось условие =l , lÎR, причем, если l>0, то , если же l<0, то 
Векторный базис на плоскости. Координаты вектора
Определение 3. Векторным базисом на плоскости называют два неколлинеарных ненулевых вектора, выходящие из одной точки и взятые в определенном порядке, например, 
и 
Тогда любой вектор на плоскости можно разложить в этом базисе 
|
|
|
Это означает, что если на плоскости выбран базис (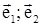
), то каждому вектору этой плоскости однозначно сопоставлена упорядоченная пара чисел х и y и наоборот. Числа x и y называют координатами вектора в базисе (
), при этом пишут 
.
Определение 4. Базис (
) на плоскости называют ортонормированным, если базисные вектора единичны и взаимно перпендикулярны 
=1, 
. Данный базис задает прямоугольную декартову систему координат. Векторы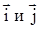 
называют ортами.
Любой вектор плоскости можно представить в виде разложения по базису (
) = 
где x и y называют прямоугольными координатами вектора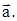 
Рассмотрим вектор , где А(
), В(
), тогда координаты определяются разностью одноименных координат точек В и А, т. е. 
.
|
|
|
