 |
Оценка случайной погрешности. Доверительный интервал
|
|
|
|
Методика оценки случайной погрешности основана на положениях теории вероятностей и математической статистики. Оценить случайную ошибку можно только в том случае, когда проведено неоднократное измерение одной и той же величины.
Пусть в результате проделанных измерений получено п значений величины х: х 1 , х 2 , …, хп. Обозначим через 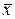 среднеарифметическое значение
среднеарифметическое значение
 . (3)
. (3)
В теории вероятностей доказано, что при увеличении числа измерений п среднеарифметическое значение измеряемой величины приближается к истинному:

При небольшом числе измерений (п £ 10) среднее значение может существенно отличаться от истинного. Для того, чтобы знать, насколько точно значение 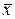 характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
характеризует измеряемую величину, необходимо определить так называемый доверительный интервал полученного результата.
Поскольку абсолютно точное измерение невозможно, то вероятность правильности утверждения «величина х имеет значение, в точности равное 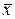 » равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью a (0 < a < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина a – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3).
» равна нулю. Вероятность же утверждения «величина х имеет какое-либо значение» равна единице (100%). Таким образом, вероятность правильности любого промежуточного утверждения лежит в пределах от 0 до 1. Цель измерения – найти такой интервал, в котором с наперед заданной вероятностью a (0 < a < 1) находится истинное значение измеряемой величины. Этот интервал называется доверительным интервалом, а неразрывно связанная с ним величина a – доверительной вероятностью (или коэффициентом надежности). За середину интервала принимается среднее значение, рассчитанное по формуле (3).
Очевидно, что ширина доверительного интервала (а следовательно, и ошибка D s x) зависит от того, насколько сильно отличаются отдельные измерения величины хi от среднего значения 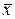 . «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой s, которую находят по формуле
. «Разброс» результатов измерений относительно среднего характеризуется среднеквадратичной ошибкой s, которую находят по формуле
|
|
|
 , (4)
, (4)
где  .
.
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке:
 . (5)
. (5)
Коэффициент пропорциональности tn,a называется коэффициентом Стьюдента; он зависит от числа опытов п и доверительной вероятности a.
Следует отметить, что доверительная вероятность никак не связана с точностью результата измерений. Величиной a задаются заранее, исходя из требований к их надежности. В большинстве технических экспериментов и в лабораторном практикуме значение a принимается равным 0,95.
Расчет случайной погрешности измерения величины х проводится в следующем порядке:
1) вычисляется сумма измеренных значений, а затем – среднее значение величины 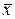 по формуле (3);
по формуле (3);
2) для каждого i -го опыта рассчитываются разность между измеренным и средним значениями  , а также квадрат этой разности (отклонения) (D хi)2 ;
, а также квадрат этой разности (отклонения) (D хi)2 ;
3) находится сумма квадратов отклонений, а затем – средне-квадратичная ошибка s по формуле (4);
4) по заданной доверительной вероятности a и числу проведенных опытов п из таблицы на с. 149 приложений выбирается соответствующее значение коэффициента Стьюдента tn,a и определяется случайная погрешность D s x по формуле (5).
Значения коэффициента Стьюдента tn,a
| a | Ч и с л о и з м е р е н и й п | ||||||||||
| 0,90 | 2,92 | 2,35 | 2,13 | 2,02 | 1,94 | 1,90 | 1,86 | 1,83 | 1,76 | 1,73 | 1,71 |
| 0,95 | 4,30 | 3,18 | 2,78 | 2,57 | 2,45 | 2,36 | 2,31 | 2,26 | 2,14 | 2,09 | 2,06 |
| 0,99 | 9,92 | 5,84 | 4,60 | 4,03 | 3,71 | 3,50 | 3,36 | 3,25 | 2,98 | 2,86 | 2,80 |
Плотность веществ r
| Вещество | Вода | Глицерин | Ртуть | Свинец |
| r, кг/м 3 |
Вязкость некоторых веществ h
| Глицерин | Т, ° С | ||||
| h, Па×с | 12,10 | 3,95 | 1,48 | 0,60 | |
| Воздух | Т, ° С | ||||
| h, мкПа×с | 17,2 | 17,9 | 18,4 | 19,6 |
|
|
|
|
|
|


