 |
Гранные геометрические тела
|
|
|
|
ТЕОРИЯ МНОГОГРАННИКОВ
Гранным геометрическим телом или многогранником называют часть пространства, ограниченную совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной другого одного многоугольника (называемого смежным), причем вокруг каждой вершины существует один цикл многоугольников. Упрощая вышеизложенное определение, получаем определение многогранника, знакомое из школьного учебника.
Многогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника.
Из истории
Греческая математика, в которой впервые появилась теория многогранников, развивалась под большим влиянием знаменитого мыслителя Платона.
Платон (427–347 до н.э.) – великий древнегреческий философ, основатель Академии и родоначальник традиции платонизма. Одним из существенных черт его учения является рассмотрение идеальных объектов - абстракций. Математика, взяв на вооружение идеи Платона, со времен Евклида изучает именно абстрактные, идеальные объекты. Однако и сам Платон, и многие древние математики вкладывали в термин идеальный не только смысл абстрактный, но и смысл наилучший. В соответствии с традицией, идущей от древних математиков, среди всех многогранников лучшие те, которые имеют своими гранями правильные многоугольники.
Многогранники можно классифицировать по нескольким признакам: например, по числу граней различают четырехгранники, пятигранники и т. д.
Различают правильные и полуправильные многогранники. Правильными называют такие многогранники, у которых все грани - правильные равные многоугольники и все углы при вершинах равны. Если гранями многогранника являются различные правильные многоугольники, то получается многогранник, который называется полуправильным (равноугольно полуправильным). Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон), и все многогранные углы равны.
|
|
|
Кроме правильных и полуправильных многогранников красивые формы имеют так называемые правильные звездчатые многогранники. Они получаются из правильных многогранников продолжением граней или ребер аналогично тому, как правильные звездчатые многоугольники получаются продолжением сторон правильных многоугольников.
Из множества многогранников выделим наиболее известные: призму и пирамиду (рис. 1).
Призмой называют многогранник, у которого две одинаковые взаимно параллельные грани - основания, а остальные - боковые грани – параллелограммы.
Пирамида представляет собой многогранник, у которого одна грань - произвольный многоугольник - принимается за основание, а остальные грани (боковые) - треугольники с общей вершиной, называемой вершиной пирамиды.
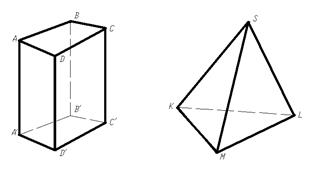
Рис. 1
На рис. 2 представлены несколько призм и пирамид. Пирамида, основание которой имеет форму треугольника, называется треугольной пирамидой. Так, можно говорить о квадратных, пятиугольных и т.д. пирамидах рис. 2, а и 2, б. Основанием треугольной пирамиды может служить любая грань.
На рис. 2, в, 2, г и 2, д приведены примеры некоторого класса многогранников, вершины которых можно разделить на два множества из одинакового числа точек; точки каждого из этих множеств являются вершинами р-угольника, причем плоскости обоих p-угольников параллельны. Если эти два р-угольника (основания) конгруэнтны и расположены так, что вершины одного р-угольника соединены с вершинами другого р-угольника параллельными прямолинейными отрезками, то такой многогранник называется р-угольной призмой. Примерами двух р-угольных призм могут служить треугольная призма (р = 3) на рис. 2, в и пятиугольная призма (р = 5) на рис. 2, г. Если же основания расположены так, что вершины одного р-угольника соединены с вершинами другого р-угольника зигзагообразной ломаной, состоящей из 2р прямолинейных отрезков, как на рис. 2, д, то такой многогранник называется р-угольной антипризмой.
|
|
|
Кроме двух оснований, у р-угольной призмы имеются р граней - параллелограммов. Если параллелограммы имеют форму прямоугольников, то призма называется прямой. У такой призмы ребра боковых граней перпендикулярны основанию. Призму, у которой основания не параллельны, называют усеченной.

Рис. 2.
2. Правильные многогранники. Выпуклый многогранник называется правильным, если он удовлетворяет следующим двум условиям:
- все его грани - конгруэнтные правильные многоугольники;
- к каждой вершине примыкает одно и то же число граней.
Если все грани правильного многогранника правильные многоугольники, то в правильных многогранниках все плоские, многогранные и двугранные углы равны.
Если все грани - правильные р-угольники и q из них примыкают к каждой вершине, то такой правильный многогранник обозначается {p, q}. Первое число в скобках указывает, сколько сторон у каждой грани, второе - число граней, примыкающих к каждой вершине. Это обозначение было предложено Л. Шлефли (1814-1895), швейцарским математиком, которому принадлежит немало изящных результатов в геометрии и математическом анализе. Существуют невыпуклые многогранники, у которых грани пересекаются и которые называются "правильными звездчатыми многогранниками". В геометрии условно под правильными многогранниками понимают исключительно выпуклые правильные многогранники
Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном.
Существует 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
|
|
|
ТЕТРАЭДР – правильный многогранник, поверхность которого состоит из четырех правильных треугольников.
ГЕКСАЭДР (КУБ) – правильный многогранник, поверхность которого состоит из шести правильных четырехугольников (квадратов
ОКТАЭДР – правильный многогранник, поверхность которого состоит из восьми правильных треугольников.
ДОДЕКАЭДР – правильный многогранник, поверхность которого состоит из двенадцати правильных пятиугольников.
ИКОСАЭДР – правильный многогранник, поверхность которого состоит из двадцати правильных треугольников.
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» - грань;
«тетра» - 4;
«гекса» - 6;
«окта» - 8;
«икоса» - 20;
«додека» - 12.
На рис. 3 изображены правильные многогранники

Рис. 3.
Из истории
Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим. Это была одна из первых попыток ввести в науку идею систематизации.
Древние греки рассматривали додекаэдр как форму Вселенной. Ими исследовались также и многие геометрические свойства платоновых тел; с плодами их изысканий можно ознакомиться по 13-й книге Начал Евклида.
Изучение платоновых тел и связанных с ними фигур продолжается и поныне. И хотя основными мотивами современных исследований служат красота и симметрия, они имеют также и некоторое научное значение, особенно в кристаллографии. Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются в природе в виде куба, тетраэдра и октаэдра соответственно. Икосаэдр и додекаэдр среди кристаллических форм не встречаются, но их можно наблюдать среди форм микроскопических морских организмов, известных под названием радиолярий.
|
|
|
Свойства правильных многогранников. Вершины любого правильного многогранника лежат на сфере (что вряд ли вызовет удивление, если вспомнить, что вершины любого правильного многоугольника лежат на окружности). Помимо этой сферы, называемой "описанной сферой", имеются еще две важные сферы. Одна из них, "срединная сфера", проходит через середины всех ребер, а другая, "вписанная сфера", касается всех граней в их центрах. Все три сферы имеют общий центр, который называется центром многогранника.
Число правильных многогранников. Естественно спросить, существуют ли кроме платоновых тел другие правильные многогранники.
Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются Начала Евклида
Как показывают следующие простые соображения, ответ должен быть отрицательным. Пусть {p, q} - произвольный правильный многогранник. Так как его гранями служат правильные р-угольники, их внутренние углы, как нетрудно показать, равны (180 - 360/р) или 180 (1 - 2/р) градусам. Так как многогранник {p, q} выпуклый, сумма всех внутренних углов по граням, примыкающим к любой из его вершин, должна быть меньше 360 градусов. Но к каждой вершине примыкают q граней, поэтому должно выполняться неравенство.
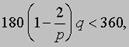
где символ < означает "меньше чем". После несложных алгебраических преобразований полученное неравенство приводится к виду

Нетрудно видеть, что p и q должны быть больше 2. Подставляя в (1) р = 3, мы обнаруживаем, что единственными допустимыми значениями q в этом случае являются 3, 4 и 5, т.е. получаем многогранники {3, 3}, {3, 4} и {3, 5}. При р = 4 единственным допустимым значением q является 3, т.е. многогранник {4, 3}, при р = 5 неравенству (1) также удовлетворяет только q = 3, т.е. многогранник {5, 3}. При p > 5 допустимых значений q не существует. Следовательно, других правильных многогранников, кроме тел Платона, не существует.
3. Полуправильные многогранники. Выше мы рассмотрели правильные многогранники, т.е. такие выпуклые многогранники, гранями которых являются равные правильные многоугольники, и в каждой вершине которых сходится одинаковое число граней. Если в этом определении допустить, чтобы гранями многогранника могли быть различные правильные многоугольники, то получим многогранники, которые называются полуправильными (равноугольно полуправильными).
|
|
|
Полуправильным многогранником называется выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон), и все многогранные углы равны.
К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны. Например, правильная пятиугольная призма на рисунке 4, а имеет своими гранями два правильных пятиугольника - основания призмы и пять квадратов, образующих боковую поверхность призмы. К полуправильным многогранникам относятся и так называемые антипризмы. На рисунке 4, б мы видим пятиугольную антипризму, полученную из пятиугольной призмы поворотом одного из оснований относительно другого на угол 36. Каждая вершина верхнего и нижнего оснований соединена с двумя ближайшими вершинами другого основания.
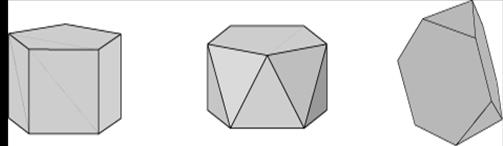
а б в
Рис. 4
Кроме этих двух бесконечных серий полуправильных многогранников имеется еще 13 полуправильных многогранников которые впервые открыл и описал Архимед - это тела Архимеда.
Самые простые из них получаются из правильных многогранников операцией "усечения", состоящей в отсечении плоскостями углов многогранника. Если срезать углы тетраэдра плоскостями, каждая из которых отсекает третью часть его ребер, выходящих из одной вершины, то получим усеченный тетраэдр, имеющий восемь граней (рис. 4, в). Из них четыре - правильные шестиугольники и четыре - правильные треугольники. В каждой вершине этого многогранника сходятся три грани.
Если указанным образом срезать вершины октаэдра и икосаэдра, то получим соответственно усеченный октаэдр (рис. 5, а) и усеченный икосаэдр (рис. 5, б). Обратите внимание на то, что поверхность футбольного мяча изготавливают в форме поверхности усеченного икосаэдра. Из куба и додекаэдра также можно получить усеченный куб (рис. 5,в) и усеченный додекаэдр (рис. 5, г).
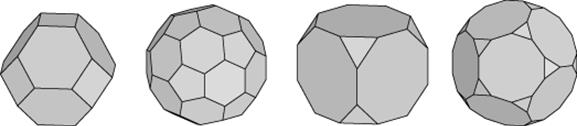
а б в г
Рис. 5
Мы рассмотрели 4 из 13 описанных Архимедом полуправильных многогранников. Оставшиеся - многогранники более сложного типа.
Из истории
Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников. Кеплер предположил, что расстояния между шестью известными тогда планетам выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой небесных сфер, по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр.
Серьезный шаг в науке о многогранниках был сделан в XVIII веке Леонардом Эйлером (1707-1783), который без преувеличения «поверил алгеброй гармонию». Теорема Эйлера о соотношении между числом вершин, ребер и граней выпуклого многогранника, доказательство которой Эйлер опубликовал в 1758 г. в «Записках Петербургской академии наук», окончательно навела математический порядок в многообразном мире многогранников.
Вершины + Грани - Рёбра = 2.
Элементы симметрии правильных многогранников
| Многогранник | Вершины | Грани | Рёбра | Оси симметрии | Плоскости симметрии |
| Тетраэдр | |||||
| Куб | |||||
| Октаэдр | |||||
| Додекаэдр | |||||
| Икосаэдр |
Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов, простейших микроорганизмов
Звездчатые многогранники
Звездчатые многогранники получаются из правильных многогранников продолжением граней или ребер аналогично тому, как правильные звездчатые многоугольники получаются продолжением сторон правильных многоугольников.
Первые два правильных звездчатых многогранника были открыты И. Кеплером (1571-1630), а два других почти 200 лет спустя построил французский математик и механик Л. Пуансо (1777-1859). Именно поэтому правильные звездчатые многогранники называются телами Кеплера-Пуансо.
В работе "О многоугольниках и многогранниках" (1810) Пуансо описал четыре правильных звездчатых многогранника, но вопрос о существовании других таких многогранников оставался открытым. Ответ на него был дан год спустя, в 1811 году, французским математиком О. Коши (1789-1857). В работе "Исследование о многогранниках" он доказал, что других правильных звездчатых многогранников не существует.
Рассмотрим вопрос о том, из каких правильных многогранников можно получить правильные звездчатые многогранники. Из тетраэдра, куба и октаэдра правильные звездчатые многогранники не получаются. Возьмем додекаэдр. Продолжение его ребер приводит к замене каждой грани звездчатым правильным пятиугольником (рис. 30,а), и в результате возникает многогранник, который называется малым звездчатым додекаэдром (рис. 30,б).

При продолжении граней додекаэдра возникают две возможности. Во-первых, если рассматривать правильные пятиугольники, то получится так называемый большой додекаэдр (рис. 31). Если же, во-вторых, в качестве граней рассматривать звездчатые пятиугольники, то получается большой звездчатый додекаэдр (рис. 32).
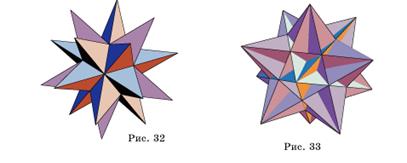
Икосаэдр имеет одну звездчатую форму. При продолжении граней правильного икосаэдра получается большой икосаэдр (рис. 33).
Таким образом, существуют 4 типа правильных звездчатых многогранников.
Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений.
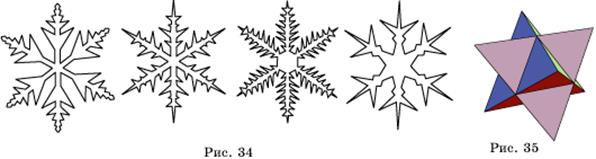
Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники (рис 34). С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.
|
|
|


