 |
Задания для контрольных работ
|
|
|
|
К.А.Зиновьев, Е.С. Рогозина, А.З. Скопец, Л.П. Щипина
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению контрольной работы по дисциплине «Математика»
для студентов 1 курса инженерного факультета заочной формы обучения
МАТЕМАТИКА
Ярославль
Порядок выполнения контрольных работ
К выполнению каждой контрольной работы следует приступать только после изучения соответствующего материала в учебной литературе, список которой дан в каждой главе, и примеров решений задач, приведенных в данном пособии. Можно также использовать ресурсы сети Internet.
При этом необходимо руководствоваться следующими указаниями:
1. Контрольную работу следует выполнять в отдельной тетради, на обложке которой должны быть указаны фамилия и инициалы студента, полный шифр, номер контрольной работы и дата её отправки в академию. Решения всех задач и пояснения к ним должны быть достаточно подробными. Все вычисления необходимо делать полностью, чертежи должны быть выполнены аккуратно и четко, с указанием координатных осей, единиц масштаба и других элементов.
2. Студент выполняет вариант контрольной работы, совпадающий с последней цифрой номера его зачетной книжки. Например, если номер зачетной книжки студента 02076, то он решает все задачи шестого варианта. Номера задач указаны в таблице 1.
3. Незачтённая работа возвращается студенту, который должен в кратчайший срок выполнить все требования рецензента и представить ее на повторное рецензирование вместе с первоначальным текстом.
Таблица 1 – Распределение задач по вариантам
| Вариант (последняя цифра номера зачетной книжки) | Номера задач | ||||||||
|
|
|
Тема 1. Аналитическая геометрия на плоскости
Примеры решения задач
Задача №1. Даны вершины треугольника АВС: А (–2; 4), В (6; –2), С (8; 7). Найти: 1) периметр треугольника; 2) уравнения сторон в общем виде; 3) внутренний угол А в градусах; 4) координаты точки пересечения медиан Q; 5)уравнение высоты АD; 6) уравнение прямой, проходящей через точку А параллельно стороне ВС; 7) составить систему неравенств, определяющую внутреннюю область треугольника АВС. Сделать чертеж.
Решение. 1) Расстояние между двумя точками А (х 1; у 1) и В (х 2; у 2) вычисляется по формуле
АВ = 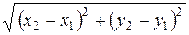 .
.
Подставив в нее координаты точек А и В, получаем:
АВ =  = 10.
= 10.
Аналогично находим ВС =  ; АС =
; АС =  . Так как периметр Р треугольника равен сумме длин его сторон, то
. Так как периметр Р треугольника равен сумме длин его сторон, то
Р = 10 +  +
+  .
.
C
A Q

2 D
E
–2 0 2 4 6 8 10 х
B
Рисунок 2 – Треугольник АВС на плоскости
2) Уравнение прямой, проходящей через точки А (х 1; у 1) и В (х 2; у 2) имеет вид
 .
.
Подставив в него координаты точек А и В, получим уравнение прямой АВ
 или 3 х + 4 у – 10 = 0.
или 3 х + 4 у – 10 = 0.
Аналогично получаем уравнения прямых АС 3 х – 10 у + 46 = 0, и ВС 9 х – 2 у – 58 = 0.
3) Для нахождения внутреннего угла А треугольника воспользуемся формулой тангенса угла между двумя прямыми
 .
.
Из рис. 1 следует, что в качестве k 1 следует взять угловой коэффициент прямой АВ, а в качестве k 2 - угловой коэффициент прямой АС. Чтобы найти угловой коэффициент прямой АВ, запишем ее уравнение в виде
|
|
|
 .
.
Тогда  . Следовательно,
. Следовательно,  . Аналогично из уравнения прямой АС 3 х – 10 у + 46 = 0 находим
. Аналогично из уравнения прямой АС 3 х – 10 у + 46 = 0 находим  . Подставив в формулу для вычисления tgA угловые коэффициенты
. Подставив в формулу для вычисления tgA угловые коэффициенты  и
и 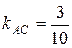 , получим:
, получим:
 .
.
Откуда 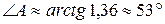 .
.
4) Известно, что точка пересечения медиан Q делит каждую из них в отношении 2:1, считая от вершины. Тогда для отрезков медианы CE имеет место равенство:  . Таким образом, координаты точки Q можно вычислить по формулам деления отрезка в данном отношении
. Таким образом, координаты точки Q можно вычислить по формулам деления отрезка в данном отношении
 ,
, 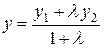 .
.
По этим формулам найдем координаты точки Е, делящей отрезок АВ пополам, при этом l = 1.
 ,
,  .
.
Итак, Е (2; 1). Воспользуемся формулами деления отрезка в данном отношении для нахождения координат точки Q, подставив в них координаты точек С и Е, при этом l = 2:

 .
.
Точка пересечения медиан треугольника Q (4; 3).
5) Высота АD перпендикулярна стороне ВС, поэтому угловые коэффициенты этих прямых обратны по величине и противоположны по знаку. Следовательно,
 . Так как
. Так как  , то
, то  .
.
Уравнение прямой, проходящей через данную точку М 1(х 1; у 1) имеет вид:
y – у 1 = k (x – x 1).
Подставив в него координаты точки А (–2; 4) и найденный угловой коэффициент  , получаем уравнение высоты АD
, получаем уравнение высоты АD
 или 2 х + 9 у – 32 = 0.
или 2 х + 9 у – 32 = 0.
6) Обозначим искомую прямую L. Так как прямая L параллельна ВС, то их угловые коэффициенты равны, k L = k BC =  . Подставим в уравнение y – у 1 = k (x – x 1) координаты точки А (–2; 4) и угловой коэффициент прямой L равный
. Подставим в уравнение y – у 1 = k (x – x 1) координаты точки А (–2; 4) и угловой коэффициент прямой L равный  и получим искомое уравнение прямой L
и получим искомое уравнение прямой L
9 х – 2 у + 26 = 0.
7) Множество точек треугольника АВС можно рассматривать как пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А, третья – прямой АС и содержит точку В.
Подставив в левую часть уравнения прямой АВ координаты точки С, получим
3×8 + 4×7 – 10 > 0.
Следовательно, неравенство, определяющее первую из этих полуплоскостей, имеет вид
3 х + 4 у – 10 > 0.
Аналогично, вторая полуплоскость определяется неравенством
9 х – 2 у – 58 < 0, третья – 3 х – 10 у + 46 > 0.
Таким образом, множество точек данного треугольника АВС определяется системой неравенств
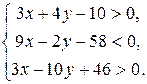
Тема 2. Введение в математический анализ
Примеры решения задач
Задача 2. Найти предел функции
|
|
|
 .
.
Решение. При непосредственной подстановке предельного значения х = 3, получаем неопределенность 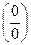 . Для раскрытия неопределенности сократим дробь
. Для раскрытия неопределенности сократим дробь  предварительно разложив на множители числитель и знаменатель дроби.
предварительно разложив на множители числитель и знаменатель дроби.
 =
=  =
=  =
=  .
.
Задача 3. Найти предел функции
 .
.
Решение. При непосредственной подстановке предельного значения х = 3, получаем неопределенность  . Для раскрытия неопределенности умножим числитель и знаменатель дроби
. Для раскрытия неопределенности умножим числитель и знаменатель дроби  на выражение, сопряженное числителю
на выражение, сопряженное числителю  . Такое преобразование даст возможность сократить дробь на множитель х –3, отличный от нуля при х ®3.
. Такое преобразование даст возможность сократить дробь на множитель х –3, отличный от нуля при х ®3.
 =
=  =
= 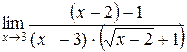 =
=
=  =
=  =
=  .
.
Задача 4. Найти предел функции
 .
.
Решение. Так как при х ® ¥ не существуют пределы числителя и знаменателя дроби  , то получаем неопределенность вида
, то получаем неопределенность вида  . Для раскрытия этой неопределенности разделим почленно числитель и знаменатель на старшую степень переменной, то есть на х 2, а затем применим теоремы о пределах.
. Для раскрытия этой неопределенности разделим почленно числитель и знаменатель на старшую степень переменной, то есть на х 2, а затем применим теоремы о пределах.
 =
=  =
= 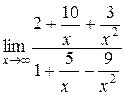 =
=
=  =
=  .
.
Задача 6. Найти предел функции
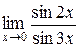 .
.
Решение. При непосредственной подстановке предельного значения х = 0, получаем неопределенность  . Для раскрытия неопределенности используем первый замечательный предел
. Для раскрытия неопределенности используем первый замечательный предел  , или, в другой форме,
, или, в другой форме,  .
.

 =
=  =
= 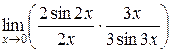 =
=
 ×
×  =
=  .
.
Задача 7. Найти предел функции
 .
.
Решение. Для нахождения предела воспользуемся вторым замечательным пределом
 .
.
Положим  , тогда
, тогда  , при этом, если
, при этом, если  , то
, то  . Получим
. Получим
 =
= 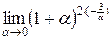 =
=  =
=  .
.
Тема 3. Производная функции и ее приложения
Примеры решения задач.
Задача 8. Найти производную функции
 .
.
Решение. Данная функция сложная и она может быть представлена в виде y = u, где
 .
.
По правилу дифференцирования сложной функции  . Для данной функции имеем
. Для данной функции имеем
 .
.
Используя формулы  и
и  , а также правила дифференцирования степенной функции
, а также правила дифференцирования степенной функции  и суммы функций, получаем
и суммы функций, получаем


=  .
.
Задача 9. Найти производную функции
 .
.
Решение. По правилу дифференцирования частного
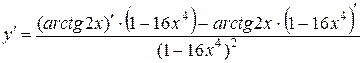 .
.
Используя далее формулы  и
и 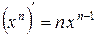 , получаем
, получаем
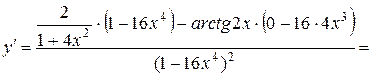

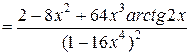 .
.
Задача 10. Найти производную функции
|
|
|
 .
.
Решение. В данном случае целесообразно вначале упростить данное выражение, используя свойства логарифмов
 =
= 
 .
.
Далее, пользуясь правилами дифференцирования и таблицей производных, получаем
 =
=
= 

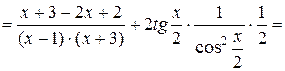
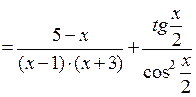 .
.
Задача 11. Найти производную функции
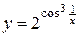 .
.
Решение. Последовательно применяя правило дифференцирования сложной функции, получим

 =
= 

= 
 .
.
Задача 12. Найти производную функции
 .
.
Решение. В данном случае функциональная зависимость задана в неявном виде. Для нахождения у ¢ нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно у ¢.
 ,
,  ,
,
 ,
,
 ,
,
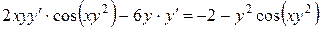 ,
,


 .
.
Задача 13. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Исследование функции предусматривает нахождение области определения, точек экстремума и интервалов возрастания и убывания, а также точек перегиба и интервалов выпуклости и вогнутости графиков функции.
1. Находим область определения функции.
Выражение  имеет смысл при любом действительном значении аргумента х, следовательно, областью определения функции является множество действительных чисел
имеет смысл при любом действительном значении аргумента х, следовательно, областью определения функции является множество действительных чисел  .
.
2. Находим первую производную заданной функции:
 или
или  .
.
3. Критическими точками функции  называются точки, в которых производная
называются точки, в которых производная  равна нулю или не существует. Найдем их.
равна нулю или не существует. Найдем их.
 , т. е.
, т. е.  или
или  , откуда
, откуда  и
и  .
.
Других критических точек нет.
Обращение производной функции в нуль или ее отсутствие в точках, где функция определена, есть лишь необходимое условие существования экстремума функции в этих точках.
Достаточным условием существования экстремума функции в критической точке является изменение знака производной первого порядка при переходе через эту точку. В частности, если производная меняет знак с плюса на минус, то в критической точке функция имеет максимум. Если же при переходе через критическую точку производная меняет знак с минуса на плюс, то в этой точке функция имеет минимум.
Определим, являются ли точки  и
и  точками экстремума. Они разбивают всю числовую ось на три промежутка, в которых определим знак производной с помощью «пробной» точки.
точками экстремума. Они разбивают всю числовую ось на три промежутка, в которых определим знак производной с помощью «пробной» точки.
В интервале (–∞; 1) возьмем точку х = 0. Тогда
 • •
• •
1 5 х
Рис. 5.
 .
.
В интервале (1; 5) возьмем точку х = 2. Имеем
 .
.
В интервале (5; ∞) – точку х = 6. В этом случае
 .
.
Итак, в точке х = 1 мы имеем максимум данной функции, а в точке х = 5 – минимум. Найдем значение функции в точках экстремума:
|
|
|
у max = y (1) =  (13 – 9∙12 + 15∙1 – 3) = 1.
(13 – 9∙12 + 15∙1 – 3) = 1.
у min = у (5) =  (53 – 9∙52 + 15∙5 – 3) = – 7.
(53 – 9∙52 + 15∙5 – 3) = – 7.
5. Если производная  функции положительна внутри некоторого промежутка, то функция
функции положительна внутри некоторого промежутка, то функция  возрастает на этом промежутке. Если же производная
возрастает на этом промежутке. Если же производная  отрицательна внутри некоторого промежутка, то функция
отрицательна внутри некоторого промежутка, то функция  убывает на этом промежутке.
убывает на этом промежутке.
Итак, данная функция возрастает на промежутках (–∞; 1) и (5; ∞), а убывает на промежутке (1; 5).Результат исследований п. 4 и п. 5 удобно представить в виде схемы.

 + – +
+ – +


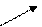
 • •
• •
 1 5 х
1 5 х
Max min
Рис. 6.
6. Найдем вторую производную у ″(х) данной функции
у ″(х) =  (3 х 2 – 18 х + 15)′ =
(3 х 2 – 18 х + 15)′ =  (6 х – 18).
(6 х – 18).
Найдем точки, в которых вторая производная функции равна нулю
 (6 х - 18) = 0, откуда х = 3.
(6 х - 18) = 0, откуда х = 3.
Точка х = 3 разбивает всю числовую ось на два интервала (–∞; 3) и (3; ∞). В интервале (–∞; 3) возьмем, например, точку х = 0 и определим в ней знак второй производной:
у ″(0) =  (6∙0 – 18) =
(6∙0 – 18) =  < 0.
< 0.
В интервале (3; ∞) возьмем, например, точку х = 4, тогда
у ″(4) =  (6∙4 – 18) =
(6∙4 – 18) =  > 0.
> 0.
Если вторая производная f ″(х) положительна внутри некоторого промежутка, то график этой функции  на этом промежутке вогнут вверх (или выпукл вниз). Если же вторая производная f ″(х) внутри некоторого промежутка отрицательна, то график функции
на этом промежутке вогнут вверх (или выпукл вниз). Если же вторая производная f ″(х) внутри некоторого промежутка отрицательна, то график функции  на этом промежутке вогнут вниз (или выпукл вверх).
на этом промежутке вогнут вниз (или выпукл вверх).
На интервале (-∞; 3) график данной функции вогнут вниз, а на промежутке (3; ∞) вогнут вверх.
7. Если вторая производная f ″(х) в некоторой точке х 0 обращается в нуль и при переходе через эту точку меняет знак, то точка  является точкой перегиба графика функции
является точкой перегиба графика функции  . Итак, х = 3 – абсцисса точки перегиба. Найдем ее ординату
. Итак, х = 3 – абсцисса точки перегиба. Найдем ее ординату
у (3) =  (33 – 9∙32 + 15∙3 – 3) =
(33 – 9∙32 + 15∙3 – 3) =  (–12) = -3.
(–12) = -3.
Таким образом, точка (3; -3) - точка перегиба графика функции.
8. Строим график функции: у =  (х 3 – 9 х 2 + 15 х – 3) (рис.7).
(х 3 – 9 х 2 + 15 х – 3) (рис.7).
 |
 1
1

 |
-2 -1 0 1 2 3 4 5 6 7
 |
 -2
-2
 -3
-3
 -4
-4


 -6
-6
-7
Рис. 7.
Задача 14. Из квадратного листа жести со стороной a требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была наибольшей?
Решение. Обозначим сторону вырезаемого квадрата за х. (Рис. 8).
 |
х х
 | ||
 |
Рис. 8.
По условию задачи х удовлетворяет неравенству 0 < х <  . Основанием получившейся коробки будет квадрат со стороной а – 2 х, высота коробки будет равна х.
. Основанием получившейся коробки будет квадрат со стороной а – 2 х, высота коробки будет равна х.
V¢(x) = a 2 – 8 ax + 12 x 2, a 2 – 8 ax + 12 x 2 = 0, откуда
 ,
,  .
.
Второй корень не удовлетворяет неравенству 0 < х <  , следовательно, сторона вырезаемого квадрата будет равна одной шестой части стороны данного листа жести, объем коробки будет наибольшим.
, следовательно, сторона вырезаемого квадрата будет равна одной шестой части стороны данного листа жести, объем коробки будет наибольшим.
Тема 4. Неопределенный интеграл
Примеры решения задач
Задача 15. Найти интеграл  .
.
Решение. Преобразуем подынтегральную функцию, а затем применяем свойства неопределенного интеграла и табличные интегралы
 и
и 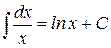 .
.
Получаем:
 =
= 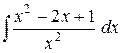 =
=  =
=  =
=
=  =
=  =
=  .
.
Задача 16. Найти интеграл  .
.
Решение. Чтобы привести данный интеграл к табличному  , положим
, положим  , тогда
, тогда  . Произведем замену в подынтегральном выражении
. Произведем замену в подынтегральном выражении
 =
=  =
=  .
.
Задача 17. Найти интеграл  .
.
Решение. Чтобы привести данный интеграл к табличному, положим  . Тогда
. Тогда  или
или  . Отсюда
. Отсюда  . Выполнив замену в подынтегральном выражении, получаем
. Выполнив замену в подынтегральном выражении, получаем
 =
=  =
=  =
=  =
=  =
=  =
=  .
.
Задача 18. Найти интеграл  .
.
Решение. Чтобы привести данный интеграл к табличному, положим  . Тогда
. Тогда  или
или  . Выполнив некоторые преобразования подынтегрального выражения, произведем замену переменной:
. Выполнив некоторые преобразования подынтегрального выражения, произведем замену переменной:
 =
=  =
=  =
=  .
.
Задача 19. Найти интеграл 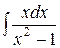 .
.
Решение. Чтобы привести данный интеграл к табличному  , положим
, положим  , тогда
, тогда  или
или  . Заметив, что числитель подынтегрального выражения отличается от дифференциала переменной t лишь на постоянный множитель, произведем замену
. Заметив, что числитель подынтегрального выражения отличается от дифференциала переменной t лишь на постоянный множитель, произведем замену
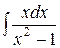 =
= 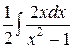 =
=  =
=  =
=  .
.
Задача 20. Найти интеграл  .
.
Решение. Для нахождения данного интеграла применим формулу интегрирования по частям:  .
.
Положим  ,
,  . Тогда
. Тогда  ,
, 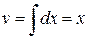 .
.
Отсюда
 .
.
В интеграле применим  подстановку
подстановку  , откуда
, откуда
 , или
, или  . Следовательно,
. Следовательно,
 =
=  =
=  =
=  .
.
Окончательно имеем: 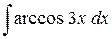
 .
.
Задача 21. Найти интеграл  .
.
Решение. Для нахождения данного интеграла также используем формулу интегрирования по частям. Положим u=x2 и dv= sin x×dx. Тогда du=2xdx и  . Отсюда
. Отсюда
 = -x 2cos x +
= -x 2cos x +  = -x2 cos x +
= -x2 cos x +  .
.
Для нахождения  опять воспользуемся методом интегрирования по частям, положив u=x, а dv=cosx dx. Тогда d u=dx и v=sinx. Окончательно получим
опять воспользуемся методом интегрирования по частям, положив u=x, а dv=cosx dx. Тогда d u=dx и v=sinx. Окончательно получим
 =
= 

Задача 22. Найти интеграл  .
.
Решение. Применяя метод интегрирования по частям, положим u= sin2 x, dv=ex dx. Тогда d u= 2cos2 x dx и v=ex. Получим
 =
= 
Для нахождения  применим метод интегрирования по частям еще раз, положив u= cos2 x, dv=ex dx. Тогда d u=- 2sin2 x dx и v=ex. Получим:
применим метод интегрирования по частям еще раз, положив u= cos2 x, dv=ex dx. Тогда d u=- 2sin2 x dx и v=ex. Получим:
 =
= 
Или:
 =
= 
Выразим искомый интеграл из полученного равенства и добавим константу интегрирования:
 + 4
+ 4  =
= 
5  =
= 
 =
=  .
.
Тема 5. Определенный интеграл
Примеры решения задач.
Задача 23. Вычислить определенный интеграл
 .
.
Решение. Данный интеграл приводится к табличному с помощью подстановки t = ln x. Отсюда  . Определим пределы интегрирования новой переменной. При х = 1, t = ln1 = 0, при х = е, t = lne = 1. Произведем замену переменной и используем формулу Ньютона–Лейбница.
. Определим пределы интегрирования новой переменной. При х = 1, t = ln1 = 0, при х = е, t = lne = 1. Произведем замену переменной и используем формулу Ньютона–Лейбница.
 =
=  =
=  = arcsin1 – arcsin0 =
= arcsin1 – arcsin0 =  .
.
Задача 24. Вычислить определенный интеграл  .
.
Решение. Преобразуем подынтегральную функцию
 =
=  =
=  =
=  .
.
Обозначим t = e x, тогда d t = e x d x. Определим пределы интегрирования новой переменной. При х = 0, t = e0 = 1, при х = 1, t = e1 = e. Тогда
 =
=  =
=  =
=  =
=
=  =
=  .
.
Задача 25. Вычислить определенный интеграл  .
.
Решение. Применим формулу интегрирования по частям для определенного интеграла
 .
.
Положим u = ln(x 2 +4), d v = d x, тогда  , v = x. Имеем
, v = x. Имеем
 =
=  =
=  =
=
= 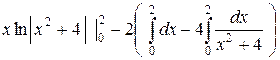 =
= 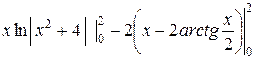 =
=
= 2 ln(4 + 4) – 0 – 2 (2 – 0 – 2arctg1 + 2 arctg0) =
= 2 ln8 – 2(2 – 2  + 2×0) = 2 ln23 – 4 + p = 6 ln2 – 4 + p.
+ 2×0) = 2 ln23 – 4 + p = 6 ln2 – 4 + p.
Задача 26. Найти площадь фигуры, ограниченной линиями:
y = x 2, 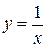 , y = 0, x = 2 (x > 0).
, y = 0, x = 2 (x > 0).
Решение. Данную фигуру можно разбить на две криволинейные трапеции, площади которых соответственно равны: S1 и S2. (Рис. 9).
Тогда S = S1 + S2. Найдем абсциссу точки А –точки пересечения двух линий.

Отсюда  , или х 4 = 1, то есть х 1 = –1 и х 2 = 1. Так как по условию x > 0, то абсцисса точки А равна 1.
, или х 4 = 1, то есть х 1 = –1 и х 2 = 1. Так как по условию x > 0, то абсцисса точки А равна 1.

 у
у

 2,0
2,0 
 1,5
1,5


 1,0
1,0
|
|
|


