Выбор стандартного состояния

Понятие об активности компонента

Рассмотренные выше разбавленные и совершенные растворы относятся к классу идеальных растворов. Уравнения, выведенные для описания этих растворов, не пригодны для термодинамического анализа реальных металлургических систем: сплавов, шлаков, штейнов и др. Особенностью таковых является наличие в них взаимодействия между частицами компонентов раствора. Именно наличие этого взаимодействия обуславливает отклонения в поведении компонентов раствора от поведения компонентов в идеальных растворах. Термодинамические уравнения, выведенные для идеальных растворов, позволяют на основе свойств компонентов предсказывать свойства раствора в целом и наоборот. Поэтому возникла задача найти такую характеристику раствор, которая могла бы связать свойства реальных растворов, и на основании которой можно было хотя бы приближённо предсказывать свойства реального раствора на основе известных свойств компонентов. Из общих соображений эта характеристика должна отвечать следующим требованиям:

- через неё должны легко выражаться термодинамические свойства раствора;

- в предельных случаях, когда реальный раствор становится идеальным, она должна совпадать с концентрацией;

- с помощью этой характеристики желательно сохранить форму уравнений, выражающих законы идеальных растворов.

Всем этим требованиям отвечает термодинамическая активность. Под термодинамической активностью понимают величину, после подстановки которой в уравнения для идеальных растворов вместо концентрации компонента, становится возможным использовать эти уравнения для термодинамического анализа реальных растворов.

Одним из основных термодинамических уравнений теории растворов является уравнение химического потенциала. Это уравнение имеет вид:

- для растворённого вещества разбавленного раствора

 

μ_i = μ + RTlnC₁; (10.1)

 

- для растворителя разбавленного раствора

 

μ₁ = μ + RTlnХ₁; (10.2)

 

- для любого компонента совершенного раствора

 

μ_i = μ + RTlnХ₁. (10.3)

 

С учётом определения термодинамической активности уравнение химического потенциала компонента реального раствора будет иметь вид:

 

μ_i = μ +RTln , (10.4)

 

где μ_i – химический потенциал i – го компонента реального раствора;

μ - стандартный потенциал i – го компонента реального раствора;

-термодинамическая активность i –го компонента реального раствора.

Из уравнения (10.1) видно, что если = 1, то μ_i = μ . Таким образом, в стандартном состоянии активность компонента реального раствора равна единице. Очевидно, что для компонентов идеальных растворов μ = μ .

Термодинамическая активность является безразмерной величиной и определяется давлением насыщенного пара компонента. Рассмотрим равновесие раствор – пар. Для условий равновесия справедливо:

 

μ_i = μ_i(газ) = μ 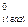+ RTlnP_i (10.5)

 

C другой стороны для стандартного состояния, как и для любого, можно записать:

 

μ = μ 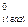+ RTlnP (10.6)

 

Вычитая из уравнения (10.5) уравнение (10.6), получим:

 

μ_i = μ + RTln (10.7)

 

Сравнение (10.7) и (10.4) даёт:

 

(10.8)

 

Таким образом, термодинамическая активность определяется как отношение давления пара компонента над реальным растворов к давлению пара этого компонента в стандартном состоянии.

 

Выбор стандартного состояния

Для расчёта активности компонента реального раствора помимо давления пара компонента над реальным раствором необходимо знать стандартное состояние этого компонента для определения давления его паров в этом состоянии. Обычно в качестве стандартного выбирается такое состояние компонента, при котором поведение реального раствора становится таким же, как и идеального. В таком состоянии активность компонента совпадает с его концентрацией.

Выберем стандартное состояние для компонентов реального раствора, близкого к совершенному раствору. Для любого компонента совершенного раствора справедлив закон Рауля:

 

Х_i = (10.9)

 

Для активности компонента реального раствора можно записать:

 

= (10.2)

 

Для стандартного состояния компонента реального раствора справедливо:

 

или = (10.3)

откуда видно, что

 

P = P (10.4)

 

Поскольку P представляет собой давление пара компонента над чистым жидким компонентом, то в качестве стандартного состояния для любого компонента реального раствора близкого к совершенному раствору принимается чистый компонент. Тогда активность компонента такого раствора будет выражаться уравнением:

 

, (10.5)

 

а закон Рауля для каждого компонента раствора уравнением:

 

P_i = _iP , (10.6)

 

где - активность i – го компонента раствора;

P_i – давление пара i – го компонента над реальным раствором;

P - давление пара i – го компонента над чистым жидким компонентом.

Рассуждая аналогичным образом, можно показать, что в качестве стандартного состояния для растворителя в реальном разбавленном растворе принимается чистый жидкий растворитель. Для него также справедливы уравнения (10.5) и (10.6).

Рассмотрим стандартное состояние для растворённого вещества реального разбавленного раствора. Для растворенного вещества идеального разбавленного раствора справедлив закон Генри:

 

С_i = Г_iР_i (10.7)

 

Активность растворённого вещества в разбавленном растворе определяется уравнением:

 

= (10.8)

 

Для стандартного состояния растворённого вещества реального разбавленного раствора справедливо:

 

или Г_iР_i = (10.9)

 

Из сравнения видно, что

 

Р = 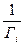(10.10)

 

Уравнение (10.10) отвечает такому состоянию реального раствора при котором начинает соблюдаться закон Генри. Тогда закон Генри для растворенного вещества будет иметь вид:

 

= Г_iP_i (10.11)

 

Количественной мерой отклонения в поведении компонентов реального раствора от поведения компонентов в идеальных растворах служит коэффициент активности компонента. Для растворителя в реальном разбавленном растворе и любого компонента реального раствора, близкого к совершенному раствору, коэффициент активности выражается уравнением:

 

γ_i = , (10.12)

 

а для растворённого вещества реального разбавленного раствора уравнением:

 

γ_i = , (10.13)

 

где γ_i – коэффициент активности i – го компонента раствора.

Если γ_i > 1, то говорят о положительном отклонении в поведении компонента от законов идеальных растворов. Если γ_i < 1, то говорят об отрицательном отклонении в поведении компонента от законов идеальных растворов. И если γ_i = 1, то имеет место идеальный раствор.

 

 

 

 

 

 

Поделиться:

Воспользуйтесь поиском по сайту: