 |
Комплексные числа. Действия над комплексными числами.
|
|
|
|
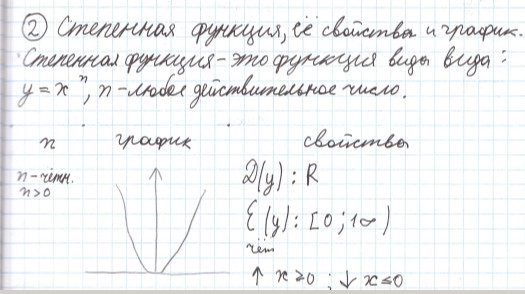
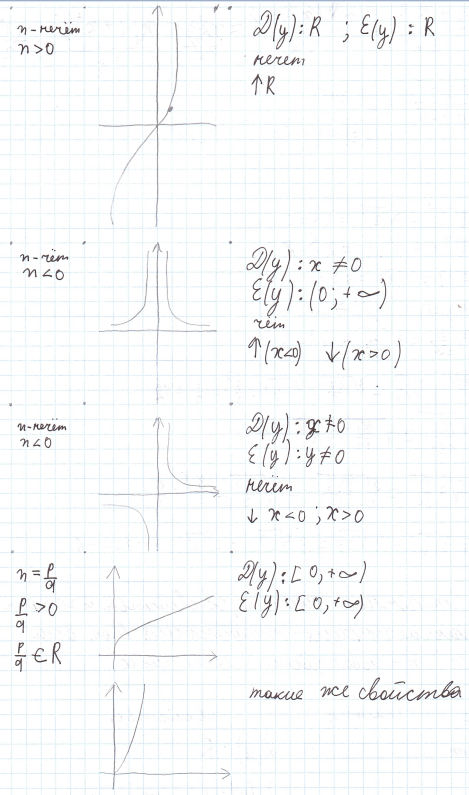
Степенная функция. Её свойства и график.
Степень числа “а” с натуральным показателем “n” – это выражение вида 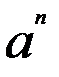 значение, которого равно произведению “n” множителей, каждый из которых равен “a”.
значение, которого равно произведению “n” множителей, каждый из которых равен “a”.
Степенью числа “a” с показателем 1 называют само число “a”.
Число, которое возводится в степень, записывают в скобках: (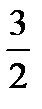 )
) 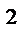
Степень числа “a” с целым положительным показателем – это степень числа с натуральным показателем: 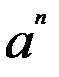 = a * a *,,, * a, где “n” целое положительное число.
= a * a *,,, * a, где “n” целое положительное число.
(под a*a*a) n раз
Свойства степеней:
1) 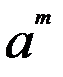 *
* 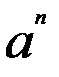 =
= 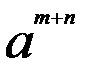 4) (a * b)
4) (a * b) 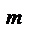 =
= 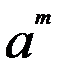 *
* 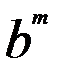 7)
7) 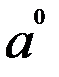 = 1
= 1
2) 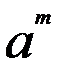 :
: 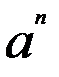 =
= 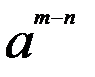 5) (
5) (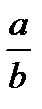 )
) 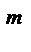 =
= 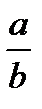
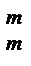
3) (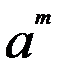 )
) 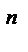 =
= 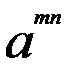 6)
6)  =
= 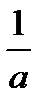
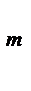
 +
+ 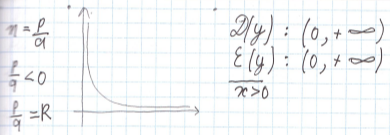
Показательная функция. Её свойства и график.
Решение показательных уравнений.
Показательным уравнениями называют уравнение вида: a 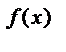 = a
= a 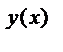 , где a > 0, a
, где a > 0, a 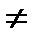 1 и уравнение сводящиеся к такому виду. Существует три основных метода решения показательных уравнений:
1 и уравнение сводящиеся к такому виду. Существует три основных метода решения показательных уравнений:
1) Функционально-графический
2) Метод уравнивания показателей
3) Метод замены (метод введения новой перемены)
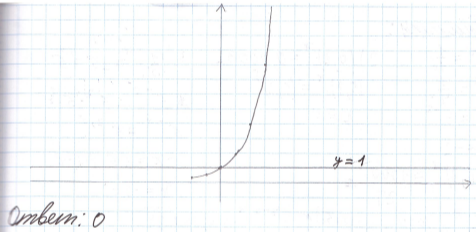
Функционально-графический метод основан на построении графика функции и нахождением им точки этих графиков, решением будет абсцисса этой точки. 
Метод уравнения показателей основан на теореме: Показательное уравнение a 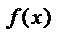 = a
= a 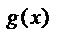 , где f(x), g(x) некоторые функции, а > 0 и a
, где f(x), g(x) некоторые функции, а > 0 и a  1
1
Показательное уравнение: a 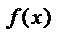 = a
= a 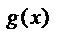 равносильно уравнению: f(x) = g(x)
равносильно уравнению: f(x) = g(x)
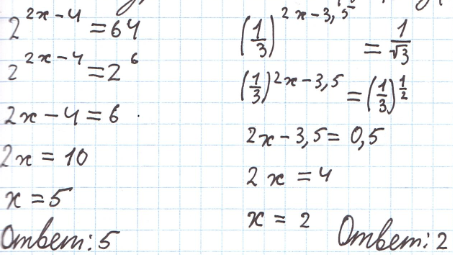
Метод замены
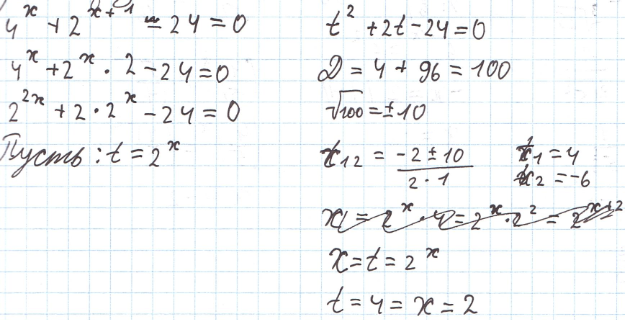
Решение показательных неравенств.
Чтобы решить показательное неравенство, нам нужно от сравнения степеней перейти к сравнению показателей.
a 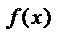 > a
> a 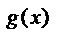
1)0 < a < 1
f(x) < g(x) |меняется знак|
2) а > 1
f(x) < g(x) |не меняется знак|
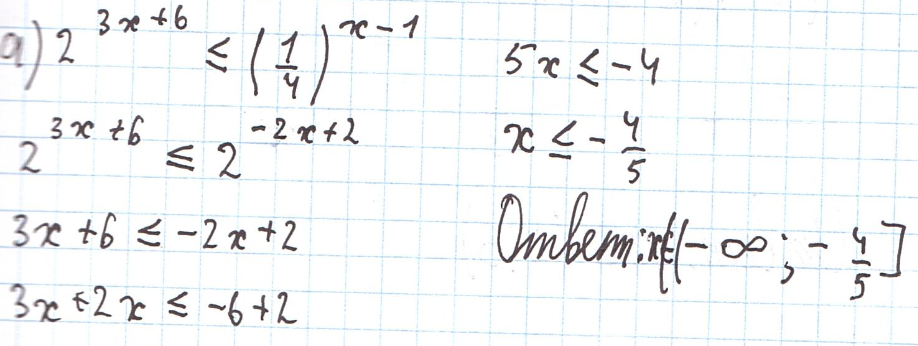
 (не забыть про ОДЗ)
(не забыть про ОДЗ)
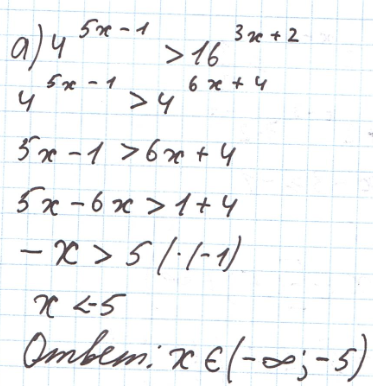
Логарифмы и их свойства.
Логарифмом числа “b” по основанию к “a”, называется показатель степени, которую нужно возвести в основание, чтобы получить число, стоящее под знаком алгорифма.
|
|
|
Log 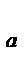 b; b > 0 | a > 0, a
b; b > 0 | a > 0, a 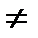 1
1
log 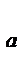 b = c
b = c
a 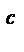 = b
= b
Свойства логарифмов:

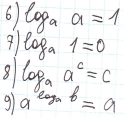
Основные логарифмические тождества.
Десятичные, натуральные логарифмы.
Операцию нахождения логарифмов, называют логарифмированием – это операция является обратной по отношению возведению в степень, соответствующим основаниям.
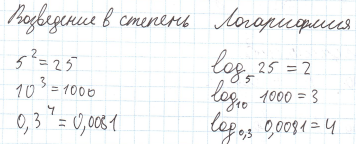
lg = Логарифм по основанию 10, обычно называют десятичным логарифмом, например:
log 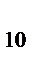 125; log
125; log 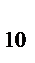 1000
1000
Также выделяют логарифм по основанию e, e примерно равно 2,71828
Называется натуральным логарифмом.
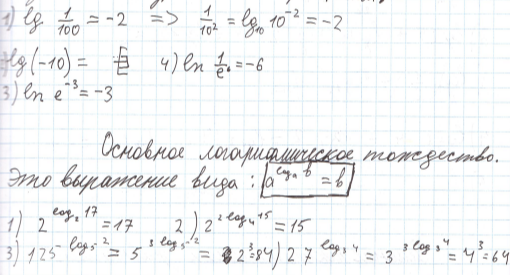
Решение логарифмических уравнений.
log  b = c b > 0
b = c b > 0
a 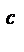 = b
= b
Логарифмическое уравнение – это уравнение, в котором не известное стоит под знаком логарифма.
Существует три основных способа решения логарифмических уравнений:
1)По определению логарифмов.
log 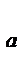 f(x) = c
f(x) = c
f(x) = a 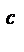
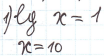
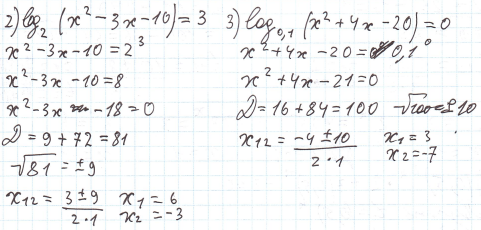
2) Потенцирование
log  f(x) = log
f(x) = log 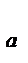 g(x)
g(x)
f(x) = g(x)
f(x) > 0
g(x) > 0
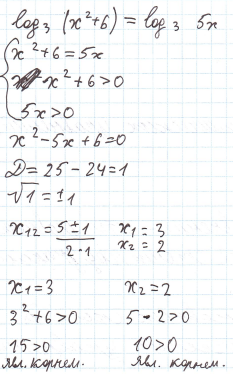
3) Метод замены

Комплексные числа. Действия над комплексными числами.
Допустим, что существует такое число, квадрат которого равен “-1”, обозначить это число “i”, тогда можно записать: i 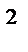 = -1
= -1
Число “i” будем называть мнимой единицой, а предыдущее равенство будем считать определением мнимой единицы. Из этого равенства следует: 1 = 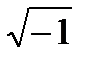
Введение понятия мнимой единицы позволяет нам теперь извлекать корни квадратные из отрицательных чисел.
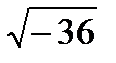 =
= 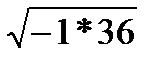 =
= 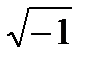 *
* 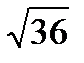 = 6i
= 6i
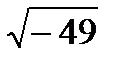 = 7i
= 7i
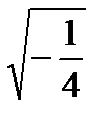 =
= 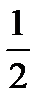 i
i
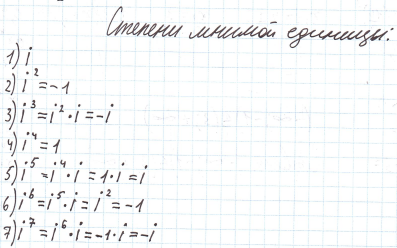
Определение комплексного числа.
Числа вида: z = a + bi, где a и b ∈ R, i – мнимая единица
Будем называть комплексные числа.
Число “a” будем называть действительной частью, “bi” мнимой частью.
Число “b” будем называть коэффициентом при мнимой части.
Выражение z = a + bi, называется алгебраической формой комплексного числа.
Возможны случаи:
1) a = 0
Z = a +bi = bi (чисто мнимое число)
2) b = 0
Z = a +bi = a (действительное число)
3) a = 0; b = 0
Z = a + bi = 0 + 0i = 0
Из этого можно сделать вывод, что действительные числа являются частным случаем комплексных чисел.
|
|
|
Два комплексных числа (z) 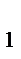 = a + bi; z
= a + bi; z 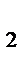 = c + di будем считать равными, тогда и только тогда a = c; b = d
= c + di будем считать равными, тогда и только тогда a = c; b = d
Пример:
Найти x,y из равенства:
3y + 5xi = 15 – 7i
3y = 15 5x = -7
Y = 5 x = - 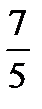
Ответ: x = - 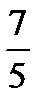 ; y = 5
; y = 5
Действия над комплексными числами в алгебраической форме.
Сложение, вычетание, умножение комплексных чисел в алгебраической форме, производят по правилам соответствующих действий над многочленами.

Два комплексных числа, называются сопряжёнными, если они отличаются друг от друга только знаками при мнимой части.
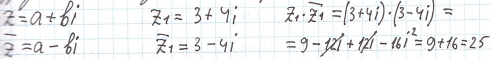
Мы видим, что произведение двух сопряжённых чисел всегда равно действительному числу. Воспользуемся этим свойством для выполнения деления двух комплексных чисел. Чтобы выполнить деление необходимо произвести дополнительное действие: умножить делимое и делитель на комплексное число, сопряжённое делителю.
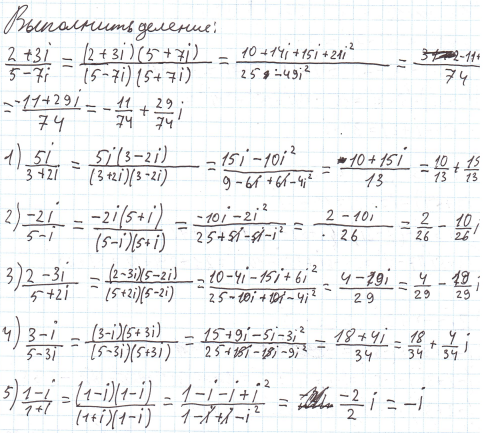
Геометрическая интерпретация комплексного числа.
Комплексное число z = a + bi можно изобразить точкой “Z” плоскости с координатами (a,b), для этого выберем на плоскости декартовую прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которые называем действительной осью, чисто мнимые числа, точками оси ординат, которую называют мнимой осью. В каждой точке плоскости с координатами (a,b), соответствует один и только один вектор с началом в точке О (0,0) и концом в точке Z (a,b), по этому комплексное число z = a + bi можно изобразить в виде вектора с началом в точке О и концом в точке Z.
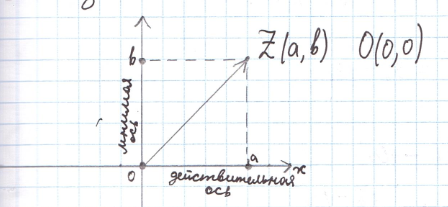
КОМПЛЕКСТНАЯ ПЛОСКОСТЬ
|
|
|


