 |
Задачи для самостоятельного решения
|
|
|
|
ПРЕДИСЛОВИЕ
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________
При изучении физики важнейшее значение имеет приобретение навыков решения задач. Именно задачи позволяют лучше понять и закрепить знание законов физики, создают представление о характерных особенностях и границах их применения. Умение решать задачи является лучшим критерием оценки глубины понимания и усвоения программного материала.
В основу любой физической задачи положен тот или иной частный случай проявления общих законов физики. Поэтому, прежде чем приступить к выполнению задания какого-либо раздела, необходимо тщательно проработать теорию. Следует помните, что без твердого знания основ теории нельзя рассчитывать на успех в выполнении даже самых простых заданий.
Цель пособия – помочь студентам научаться решать задачи по механике.
Каждый раздел состоит из следующих элементов:
· краткая теория и методические указания;
· основные законы и формулы;
· контрольные вопросы;
· примеры решения задач;
· задачи для самостоятельного решения.
При работе с данным пособием рекомендуется придерживаться следующей схемы подготовки. Прежде чем приступить к решению задач, нужно изучить теорию по рекомендованным преподавателям и программой курса учебникам или учебным пособиям. В начале каждого параграфа даются общие методические указания о наиболее рациональных методах и приемах решения задач. Далее изложены основные положения теории, приводятся важнейшие законы и формулы, применяемые при решении этих задач. Необходимо четко разобраться в физическом смысле переменных, входящих в математическое описание физических законов, ответить на контрольные вопросы, решить качественные задачи. Следует попытаться самостоятельно решить типовые задачи, рассмотренные в качестве примеров, разобрать приведенные решения, показывающие, как практически пользоваться описанными методами, решить задачи, предлагаемые в разделе для самостоятельно работы, а также предназначенные для работы в аудитории и для домашних самостоятельных занятий. К ответу имеет смысл обращаться только в том случае, если решение найдено. Числовое совпадение ответа с указанным в пособии почти наверняка означает, что ваши рассуждения были верными. Несовпадение может иметь следующие причины: а) ошибка в технике вычислений; б) неправильное применение единиц измерения; в) неверные выводы общей формулы; г) использование законов и формул, которые неприменимы при данных условиях задачи.
|
|
|
Несмотря на различие в типах задач, при их решении можно придерживаться следующих методических указаний.
1) Прочитать внимательно условие задачи, проанализировать ее исходные данные и требования, посмотреть, все ли термины в условии задачи известны и понятны. Следует помнить, что условия всех задач содержат обычно не только явные, но и скрытые данные. К скрытым данным относятся физические константы и параметры, характеризующие физические и механические свойства тел.
2) Записать краткое условие задачи, включая и скрытые данные. Правильно перевести значения данных величин в СИ. Когда введены стандартные обозначения, легче вспомнить формулы, связывающие соответствующие величины; четче видно, какие характеристики заданы, все ли они выражены в одной системе единиц.
3) Если это необходимо, сделать рисунок (схему, чертеж), на котором указать все необходимые параметры и векторы (силы, скорость, ускорение и т. п.). Рисунок позволяет более полно раскрыть содержание задачи и облегчает выявление скрытых в ней данных.
|
|
|
4) Проанализировать задачу с точки зрения того, какие физические явления и процессы в ней рассматриваются, какими законами они описываются. При этом нужно обраить особое внимание на начальное и конечное состояние рассматриваемого тела или системы тел.
5) Установить, какие физические законы, свойства и формулы могут быть использованы, выработать план решения задачи.
6) Составить в общем виде систему уравнений, связывающих искомые и заданные величины. При этом, как правило, приходится использовать дополнительные, промежуточные формулы. Если в условии задачи идет речь о векторных физических величинах, то сначала целесообразно записать векторное уравнение, а затем, выбрав направления координатных осей, перейти к скалярным уравнениям, содержащим проекции векторов.
7) Решить полученную систему уравнений в общем виде, причем искомая величина должна быть выражена через заданные величины. Применить к конечной формуле правило размерностей. Если это возможно, исследовать поведение решения в предельных случаях, убедившись в его непротиворечивости физическому смыслу задачи.
8) Подставить в полученную формулу численные значения входящих в нее физических величин в системе СИ и, выполнив необходимые математические операции, получить численный результат. Чтобы облегчить определение порядка вычисляемой величины, полезно представить исходные величины в виде чисел, близких к единице, умноженных на 10 в соответствующей степени. При вычислениях следуйте правилам действий с приближенными числами, помня, что точность вычислений должна соответствовать точности исходных данных.
9) Проанализировать полученный ответ как с точки зрения правильности размерности искомой величины, так и физической правдоподобности численного значения. Для исправления ошибки сначала надо проверить расчеты и, если они верны, то тогда еще раз проверить решение и математические преобразования.
КИНЕМАТИКА
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________
Краткая теория и методические указания
Закон движения системы точек – зависимость их координат от времени. Если закон движения известен, то с помощью простых математических операций можно найти соответствующие характеристики: скорость как функцию времени, время, за которое точка проходит определенный отрезок пути и т. д. Основной задачей кинематики является исследование характеристик движения системы точек или одной точки без учета природы сил, вызывающих это движение.
|
|
|
Одной из простых, но практически важных задач исследования движения точки является нахождение уравнений, описывающих в пространстве линию движения точки, т. е. ее траекторию. В начале необходимо сделать чертеж, выбрать систему координат, связанную с телом отсчета, отобразить траекторию движения, векторы скорости, ускорения, перемещения. Далее следует составить для данного движения уравнения, отражающие в векторной форме математическую связь между изображенными на схеме физическими величинами. Для получения расчетных формул нужно записать эти уравнения в скалярной форме, т. е. в проекциях на координатные оси.
Приступая к решению задач, в первую очередь необходимо в условии задачи увидеть те признаки, по которым можно судить о законе движения. Если описываемое в задаче движение сложно и не относится к одному из известных видов, то, вероятно, его можно разложить на совокупность более простых движений. Для этого систему координат нужно выбрать так, чтобы движение вдоль их осей можно было описывать наиболее просто. Таким образом, удачный выбор системы координат может существенно помочь решению задачи. Обязательно нужно обращать внимание на дополнительные данные, выявленные при анализе задачи (например, одновременность начала движения тел, равенство координат тел в момент их встречи и т. п.)
Важным разделом является кинематика вращательного движения. Рассмотрим движение точки по окружности. Оно может происходить или под действием специальных сил взаимодействия, или при наличии связи. Связь, наложенная на точку, такова, что точка может совершать только вращательное движение (например, маятник, точка, находящаяся на вращающемся диске, и т. д.).
|
|
|
Положение точки А на окружности удобно определять углом поворота  который образован радиусом
который образован радиусом  направленным из центра окружности О и связанным с точкой А, и некоторым начальным фиксированным радиусом
направленным из центра окружности О и связанным с точкой А, и некоторым начальным фиксированным радиусом  . В этом случае вводят угловую скорость
. В этом случае вводят угловую скорость  . Повернувшись на малый угол
. Повернувшись на малый угол  , точка пройдет по малой дуге расстояние
, точка пройдет по малой дуге расстояние  . Поэтому
. Поэтому  . Но
. Но  есть значение линейной скорости движения точки, направленной по касательной к окружности. Следовательно,
есть значение линейной скорости движения точки, направленной по касательной к окружности. Следовательно,  При равномерном вращении угловая скорость постоянна, т. е.
При равномерном вращении угловая скорость постоянна, т. е.  поэтому
поэтому  Часто считается, что точка А в начальный момент времени
Часто считается, что точка А в начальный момент времени  находится в точке x, т.е.
находится в точке x, т.е.  . Постоянная угловая скорость
. Постоянная угловая скорость  называется угловой (циклической) частотой вращения.
называется угловой (циклической) частотой вращения.
Даже если точка движется по окружности с постоянной угловой скоростью, у нее есть ускорение, так как направление вектора скорости  меняется. Это ускорение называется центростремительным (нормальным) и выражается формулой
меняется. Это ускорение называется центростремительным (нормальным) и выражается формулой  (отрицательный знак соответствует направлению ускорения к центру окружности). Если угловая скорость непостоянна, то имеется угловое ускорение
(отрицательный знак соответствует направлению ускорения к центру окружности). Если угловая скорость непостоянна, то имеется угловое ускорение 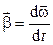 .
.
Основные законы и формулы
Если пространство отнесено к некоторой неподвижной (относительно наблюдателя) прямоугольной декартовой системе координат XYZ,то положениематериальной точки в пространстве определяется ее радиусом-вектором

где  ,
,  ,
,  –координаты вектора
–координаты вектора 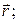
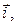

 – координатные орты.
– координатные орты.
Движение материальной точки описывается кинематическим законом

где 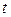 – время.
– время.
Скорость  и ускорение
и ускорение 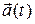 материальной точки определяются формулами
материальной точки определяются формулами
 ;
;  .
.
В случае прямолинейного равномерного движения 

В случае прямолинейного равнопеременного движения ( )
)


где  – начальная скорость в момент времени
– начальная скорость в момент времени 
 – перемещение тела.
– перемещение тела.
При криволинейном движении вектор скорости в каждой точке траектории совпадает с направлением касательной к траектории в этой же точке. Ускорение при криволинейном движении разлагается на две составляющие: тангенциальное (или касательное) ускорение  и нормальное (или центростремительное) ускорение
и нормальное (или центростремительное) ускорение  . Тангенциальное ускорение характеризует изменение скорости по величине, оно направлено по касательной и выражается формулой
. Тангенциальное ускорение характеризует изменение скорости по величине, оно направлено по касательной и выражается формулой 
Нормальное ускорение характеризует изменение скорости по направлению, оно направлено к центру кривизны траектории  и выражается формулой
и выражается формулой 
Полное ускорение
 ,
,
а направление полного ускорения определяется углами, которые оно образует с радиусом кривизны или с касательной (направляющие косинусы).
При вращательном движении в общем случае угловая скорость
 ,
,
где  – угол, описываемый радиус-вектором за время
– угол, описываемый радиус-вектором за время 
|
|
|
Угловая  и линейная
и линейная  скорости любой точки вращающегося твердого тела связаны соотношением
скорости любой точки вращающегося твердого тела связаны соотношением
 ,
,
где  – радиус-вектор рассматриваемой точки относительно произвольной точки оси вращения.
– радиус-вектор рассматриваемой точки относительно произвольной точки оси вращения.
Угловое ускорение
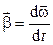 .
.
В случае равномерного вращательного движения угловая скорость

где  – период вращения,
– период вращения,  – частота вращения.
– частота вращения.
Тангенциальное и нормальное ускорения при вращательном движении могут быть выражены следующим образом:


Связь между скоростями материальной точки относительно двух различных систем отсчета выражается законом сложения скоростей

где  – скорость точки относительно неподвижной системы отсчета;
– скорость точки относительно неподвижной системы отсчета;  –скорость этой же точки относительно движущейся системы отсчета;
–скорость этой же точки относительно движущейся системы отсчета;  –скорость движущейся системы отсчета относительно неподвижной.
–скорость движущейся системы отсчета относительно неподвижной.
Контрольные вопросы
1. Какие системы координат Вам известны? Из каких соображений должна выбираться система координат для описания того или иного круга явлений?
2. Какие способы описания движения Вы знаете?
3. В чем состоят преимущества векторных обозначений и векторной записи движения?
4. По каким правилам вводится вектор перемещения?
5. Чем отличается перемещение от пути?
6. В каком случае модуль перемещения и пути совпадают?
7. Что такое мгновенная скорость и как она ориентирована относительно траектории?
8. Как связаны компоненты скорости и ускорения материальной точки с производными ее координат по времени?
9. Как найти соотношения между векторами угловой и линейной скорости?
10. Какие два простейших вида движения лежат в основе любых более сложных?
11. Каковы направления нормального и тангенциального ускорений относительно траектории и чем определяется их абсолютное значение?
12. Может ли криволинейное движение быть равномерным?
13. Откуда следует, что угловая скорость является вектором?
14. Чему равно скалярное произведение скорости и ускорения в случае равномерного движения по окружности?
15. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?
16. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?
17. Что такое вектор углового ускорения? Как он направлен, если угловая скорость неизменна по направлению?
18. Сформулируйте первую и вторую задачи кинематики для материальной точки. Какую роль играют начальные условия при попытках предсказать характер движения тела и его местонахождение через заданный промежуток времени от начала?
19. Что представляет собой траектория кончика винта летящего самолета в системе отсчета, связанной с: а) самолетом; б) поверхностью Земли?
20. Почему дождевые капли в безветренную погоду оставляют наклонные полосы на стеклах окон равномерно движущегося автобуса? От чего зависит угол наклона полос?
21. Эскалатор метро движется вверх. С какой скоростью и в каком направлении необходимо двигаться человеку по этому эскалатору, чтобы быть неподвижным относительно перрону?
22. Может ли астронавт для измерения скорости воздушного шара использовать парус?
23. Могут ли средняя и мгновенная скорости быть равными между собой?
24. Шарик свободно падает без начальной скорости с высоты  на горизонтальную поверхность. Изобразите график координаты, пути и скорости шарика. Считайте, что при соударении шарика с поверхностью направление его скорости изменяется на противоположное, а ее модуль остается неизменным. Продолжительность удара пренебрежимо мала.
на горизонтальную поверхность. Изобразите график координаты, пути и скорости шарика. Считайте, что при соударении шарика с поверхностью направление его скорости изменяется на противоположное, а ее модуль остается неизменным. Продолжительность удара пренебрежимо мала.
25. Тяжелый шарик с помощью нити поднимается ускоренно вверх. Как будет двигаться шарик после обрыва нити? Нарисуйте графики координаты, пути, скорости и ускорения шарика.
26. Чему равны периоды вращения минутной и часовой стрелок часов?
27. Точка движется по окружности с постоянной по модулю линейной скоростью. За какую долю периода она проходит путь, равный радиусу окружности?
28. Точка движется по окружности с постоянной по модулю линейной скоростью. За какую долю периода модуль перемещения точки равен
радиусу окружности?
29. Определите ускорение, с которым шарик движется по наклонному желобу. Имеются желоб, шарик, линейка, секундомер, штатив.
30. Определите скорость падения шарика на дно сосуда с маслом. Имеются высокий сосуд с маслом, алюминиевый шарик, линейка, секундомер.
Примеры решения задач
Задача 1
Туристу необходимо попасть из пункта А, находящегося на реке, в пункт В, находящийся в лесу. Расстояние между ними  . Часть пути турист может преодолеть на плоту. Скорость плота
. Часть пути турист может преодолеть на плоту. Скорость плота  , скорость движения туриста по лесу
, скорость движения туриста по лесу 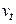 . Найти наименьшее время, за которое турист попадет из А в В. Какое расстояние он преодолеет при этом, если В находится на расстоянии
. Найти наименьшее время, за которое турист попадет из А в В. Какое расстояние он преодолеет при этом, если В находится на расстоянии  от реки?
от реки?

Рис. 1.1
Решение.
Чтобы найти наименьшее время, которое проведет турист в пути, необходимо записать функцию зависимости времени от пути и проанализировать ее. Предположим, что часть пути турист проплывет на плоту со скоростью  , затем, на расстоянии
, затем, на расстоянии  от точки С турист оставит реку и пойдет по лесу со скоростью
от точки С турист оставит реку и пойдет по лесу со скоростью 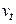 (рис. 1.1). Тогда расстояние ВС равно
(рис. 1.1). Тогда расстояние ВС равно  . В таком случае, расстояние
. В таком случае, расстояние 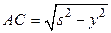 . Время в пути запишем как:
. Время в пути запишем как:
 .
.
Для нахождения минимального времени необходимо проанализировать полученную функцию на экстремумы и найти минимум. Первая производная должна равняться нулю:
 .
.
Отсюда,  .
.
Для того чтобы определить, является ли полученная точка максимумом или минимумом функции времени, проанализируем вторую производную функции в данной точке:
 .
.
Следовательно, функция в данной точке имеет минимум.
Подставив полученное значение  в функцию времени, получим значение наименьшего времени пути:
в функцию времени, получим значение наименьшего времени пути:
 .
.
Найдем расстояние, пройденное туристом, подставляя значение  в выражение:
в выражение:
 .
.
Ответ:  ;
; 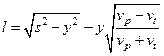 .
.
Задача 2
Материальная точка движется в плоскости  со скоростью
со скоростью  где
где  – положительные константы,
– положительные константы,  – орты координатных осей. Определить: 1) вид траектории; 2) скорость и ускорение в верхней точке траектории, если в начальный момент времени
– орты координатных осей. Определить: 1) вид траектории; 2) скорость и ускорение в верхней точке траектории, если в начальный момент времени  .
.
Решение.
Согласно условию задачи
 (1.1)
(1.1)
 . (1.2)
. (1.2)
Умножая уравнение (1.1) на  а уравнение (1.2) на
а уравнение (1.2) на  и складывая их, приходим к уравнению траектории:
и складывая их, приходим к уравнению траектории:
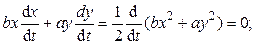

где  – некоторая константа. Из начальных условий следует, что
– некоторая константа. Из начальных условий следует, что  . Поэтому уравнение траектории имеет вид
. Поэтому уравнение траектории имеет вид

Это уравнение эллипса с полуосями, равными 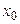 и
и  . В верхней точке траектории
. В верхней точке траектории  ,
,  Следовательно, скорость в этой точке
Следовательно, скорость в этой точке

Находим теперь проекции ускорения как функции координат:
 ;
;  .
.
Поэтому в верхней точке

Отсюда ускорение в верхней точке траектории

Ответ: 
Задача 3
Максимальная дальность полета камня, выпущенного из неподвижной катапульты, равна  м. Найти максимально возможную дальность полета камня, выпущенного из этой же катапульты, установленной на платформе, которая движется горизонтально с постоянной скоростью
м. Найти максимально возможную дальность полета камня, выпущенного из этой же катапульты, установленной на платформе, которая движется горизонтально с постоянной скоростью  м/c.
м/c.
Решение.
Вначале рассмотрим случай, когда катапульта неподвижна. В этом
случае максимальная дальность полета будет тогда, когда камень вылетает под углом 45°. Тогда дальность полета:
 (1.3)
(1.3)
а уравнение подъема камня по вертикали:
 (1.4)
(1.4)
В момент падения камня 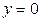 , тогда
, тогда
 (1.5)
(1.5)
Подставляя (1.5) в (1.3), получаем:

Отсюда  15 м/с (1.6)
15 м/с (1.6)
Теперь перейдем к случаю, когда катапульта движется на платформе (рис. 1.2). Начало координат совместим с положением катапульты в момент вылета камня. Здесь следует сделать одно замечание. Факт, что максимальная дальность полета достигается при угле, равном 45° имеет ограниченные рамки применения и справедлив тогда, если: а) не учитывать сопротивление воздуха; б) точка вылета и точка падения находятся на одном уровне; в) метательный снаряд неподвижен. Допустим, что катапульта выбрасывает камень под углом a к горизонту.
В этом случае проекции скорости равны
 (1.7) (1.7)
 (1.8)
Подставляя (1.8) в уравнение (1.4), находим, что в этом случае время полета камня равно: (1.8)
Подставляя (1.8) в уравнение (1.4), находим, что в этом случае время полета камня равно:

|  Рис. 1.2
Рис. 1.2
|
а уравнение (1.3) с учетом (1.7) будет иметь вид:

 . (1.9)
. (1.9)
Из условия, что когда  максимальна, производная от
максимальна, производная от  по углу должна быть равна нулю:
по углу должна быть равна нулю:
 (1.10)
(1.10)
Учитывая, что  и
и  , из (1.10) получаем
, из (1.10) получаем
 . (1.11)
. (1.11)
Решая это квадратичное уравнение относительно  , находим, что
, находим, что  или 1/2. Из условия задачи следует, что требуемое значение
или 1/2. Из условия задачи следует, что требуемое значение  , т. е. a = 60°. Тогда, подставляя найденное значение угла в уравнение (1.9), вычисляем
, т. е. a = 60°. Тогда, подставляя найденное значение угла в уравнение (1.9), вычисляем  58,5 м.
58,5 м.
Ответ:  58,5 м.
58,5 м.
Задача 4
Материальная точка движется по окружности c радиусом R со скоростью  , где s – пройденный путь;
, где s – пройденный путь;  – положительная константа. Найти: 1) зависимость пути от времени; 2) величину ускорения как функцию скорости.
– положительная константа. Найти: 1) зависимость пути от времени; 2) величину ускорения как функцию скорости.
Решение.
Согласно условию задачи
 .
.
Разделяя переменные, имеем

Проинтегрируем это уравнение:

 (1.12)
(1.12)
Полагая, что s = 0 при t = 0, из уравнения (1.12) получаем C = R. Следовательно,
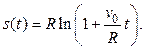
Находим тангенциальную и нормальную проекции ускорения:
 ;
;

Найдем величину ускорения как функцию скорости:
 .
.
Ответ: 1)  ; 2)
; 2)  .
.
Задача 5
Движение груза А определяется законом  (
( – в см,
– в см, 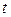 – в секундах). Груз приводит в движение вал С радиусом
– в секундах). Груз приводит в движение вал С радиусом  . На вал насажен шкив Н радиусом
. На вал насажен шкив Н радиусом  , связанный гибкой передачей со шкивом Е радиусом
, связанный гибкой передачей со шкивом Е радиусом  . Найти скорость, нормальное, тангенциальное, полное ускорение точки М обода шкива Е в момент, когда груз А, привязанный к перекинутой через блок В веревке, пройдет путь
. Найти скорость, нормальное, тангенциальное, полное ускорение точки М обода шкива Е в момент, когда груз А, привязанный к перекинутой через блок В веревке, пройдет путь 

Рис. 1.3
Решение.
 – обобщенная координата механизма, изображенного на рис. 1.3. Проскальзывание между веревкой и валом отсутствует, поэтому линейная скорость точек поверхности вала
– обобщенная координата механизма, изображенного на рис. 1.3. Проскальзывание между веревкой и валом отсутствует, поэтому линейная скорость точек поверхности вала  равна скорости движения груза А:
равна скорости движения груза А:

Угловая скорость вращения вала

Вал С и шкив Н соединены жестко, следовательно, вращаются с одинаковой угловой скоростью 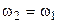 . Шкивы Н и Е связаны гибкой передачей, поэтому линейные скорости точек обода этих шкивов одинаковы:
. Шкивы Н и Е связаны гибкой передачей, поэтому линейные скорости точек обода этих шкивов одинаковы:
 ,
,  ,
,
откуда

Скорость точки М, находящейся на ободе шкива Е,

По скорости  найдем закон движения точки М. Так как
найдем закон движения точки М. Так как  , то
, то
 .
.
Нормальное, тангенциальное и полное ускорения точки М соответственно равны:
 ,
,
 ,
,
 .
.
Угловое ускорение шкива Е
 .
.
Момент времени  , когда груз А пройдет путь
, когда груз А пройдет путь  соответствует
соответствует 
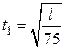 . Подставляя
. Подставляя  в соотношения, определяющие
в соотношения, определяющие  ,
,  ,
,  найдем их искомые значения.
найдем их искомые значения.
Ответ:  ,
,  ,
,  ,
,  .
.
Задача 6
Колесо равномерно катится по горизонтальной плоскости вокруг оси. Ось закреплена шарнирно в точке О, которая находится на высоте, равной радиусу колеса  . Скорость верхней точки колеса . Скорость верхней точки колеса 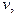 длина оси длина оси  Найти угловую скорость и угловое ускорение движения колеса. Найти угловую скорость и угловое ускорение движения колеса.
|  Рис. 1.4
Рис. 1.4
|
Решение.
Колесо участвует одновременно в двух вращательных движениях. С одной стороны колесо вращается вокруг своего центра со скоростью  , с другой стороны, ось колеса совершает вращательное движение вокруг точки О со скоростью
, с другой стороны, ось колеса совершает вращательное движение вокруг точки О со скоростью  (рис. 1.5).
(рис. 1.5).
Колесо вращается вокруг своей оси по часовой стрелке, а ось вращается вокруг точки О против часовой стрелки. Как видно из рис. 1.5, вектор скорости  направлен по оси колеса к точке О. А вектор скорости направлен перпенди-кулярно, от точки О вертикально вверх. направлен по оси колеса к точке О. А вектор скорости направлен перпенди-кулярно, от точки О вертикально вверх.
|  Рис. 1.5
Рис. 1.5
|
Таким образом, угловая скорость колеса 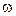 как вектор является геометрической суммой двух векторов скоростей
как вектор является геометрической суммой двух векторов скоростей  и
и  . Поскольку эти вектора перпендикулярны, то
. Поскольку эти вектора перпендикулярны, то
 .
.
Скорость  определяется как отношение линейной скорости центра колеса
определяется как отношение линейной скорости центра колеса  к расстоянию до оси вращения, т. е. к его радиусу. Скорость
к расстоянию до оси вращения, т. е. к его радиусу. Скорость  определяется как отношение линейной скорости центра колеса
определяется как отношение линейной скорости центра колеса  к расстоянию до оси вращения, т. е. к длине оси. Учитывая, что линейная скорость центра колеса вдвое меньше скорости верхней точки, получаем:
к расстоянию до оси вращения, т. е. к длине оси. Учитывая, что линейная скорость центра колеса вдвое меньше скорости верхней точки, получаем:
 ,
,  ,
,  .
.
Тогда  .
.
Несмотря на то, что обе угловые скорости  и
и  постоянны по модулю, в системе возникает угловое ускорение. Вектор угловой скорости
постоянны по модулю, в системе возникает угловое ускорение. Вектор угловой скорости  вращается вокруг вертикальной оси, проходящей через точку О. Ускорение в системе определяет изменение направления вектора угловой скорости
вращается вокруг вертикальной оси, проходящей через точку О. Ускорение в системе определяет изменение направления вектора угловой скорости  .
.
Совместим концы векторов  и
и  в точке О. Систему отсчета выберем таким образом, что в начальный момент времени вектор
в точке О. Систему отсчета выберем таким образом, что в начальный момент времени вектор  направлен по оси ОХ, а вектор
направлен по оси ОХ, а вектор  направлен по оси OZ. Вектор
направлен по оси OZ. Вектор  вращается вокруг оси OZ. В некоторый момент времени он повернется на угол
вращается вокруг оси OZ. В некоторый момент времени он повернется на угол  . В таком случае проекции угловой скорости колеса на оси запишутся как
. В таком случае проекции угловой скорости колеса на оси запишутся как
 ,
,  ,
,  .
.
С учетом того, что  , проекции углового ускорения можно найти как
, проекции углового ускорения можно найти как

 ,
, 
В таком случае, полное ускорение равно

Ответ:  ,
,  .
.
Задачи для самостоятельного решения
1.1. Точка прошла половину пути со скоростью  . На оставшейся части пути она половину времени двигалась со скоростью
. На оставшейся части пути она половину времени двигалась со скоростью  , а последний участок прошла со скоростью
, а последний участок прошла со скоростью  . Найти среднюю за все время движения скорость точки.
. Найти среднюю за все время движения скорость точки.
Ответ:  .
.
1.2. Все звезды, в частности и некоторая звезда N, удаляются от Солнца со скоростями, пропорциональными их расстоянию до него. Как будет выглядеть эта картина с «точки зрения» звезды N.
Ответ: аналогично.
1.3. Две частицы, 1 и 2, движутся с постоянными скоростями 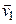 и
и  . Их радиу-векторы в начальный момент равны
. Их радиу-векторы в начальный момент равны 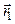 и
и  . При каком соотношении между этими четырьмя векторами частицы испытают столкновение друг с другом?
. При каком соотношении между этими четырьмя векторами частицы испытают столкновение друг с другом?
Ответ:  .
.
1.4. От бакена, который находится на середине широкой реки, отошли две лодки, A и B. Они стали двигаться по взаимно перпендикулярным прямым: лодка A – вдоль реки, а лодка B – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись обратно. Найти отношение времен движения лодок  если скорость каждой лодки относительно воды в
если скорость каждой лодки относительно воды в  раза больше скорости течения.
раза больше скорости течения.
Ответ:  .
.
1.5.Из пункта А, находящегося на шоссе, необходимо за кратчайшее время попасть в пункт В (рис. 1.6), расположенный в поле на расстоянии  от шоссе. Известно, что скоростьмашины по полю в < от шоссе. Известно, что скоростьмашины по полю в <
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

