 |
Рекомендации по выполнению лабораторных работ
|
|
|
|
К каждому выполняемому эксперименту нужно относиться как к небольшому самостоятельному научному исследованию. Описания задач — только стержни, вокруг которых строится работа. Конкретное содержание, лабораторной работы, объем навыков и сведений, извлекаемых из нее, определяются главным образом не описанием, а подходом студента к ее выполнению. Самое ценное, что может дать практикум, — умение обдумывать свои опыты, применять теоретические знания в экспериментальной работе, правильно планировать эксперимент и избегать ошибок, видеть важные и интересные особенности и казалось бы мелочи, из которых нередко получаются потом серьезные научные исследования. Все эти навыки студент должен развить в себе сам в процессе упорного, вдумчивого, сознательного и сосредоточенного труда.
Результатом выполненной работы является отчет, который должен содержать:
1) 
 описание теоретических предпосылок выполняемого эксперимента с
описание теоретических предпосылок выполняемого эксперимента с
кратким выводом необходимых формул и соотношений;
2) схему экспериментальной установки;
3) словесное описание хода эксперимента и таблицы для записи экспе-
риментальных данных;
4) обработку результатов: вычисление расчетных величин и заполнение таблиц, построение графиков, вычисление результата эксперимента;
5) сравнение полученных результатов с известными (в литературе и справочниках), обсуждение возможных ошибок, предложения по улучшению эксперимента.
Подготовка к работе. Вначале нужно внимательно прочитать описание работы и теоретическое введение по ее тематике. Это необходимо, чтобы получить представление о явлениях, закономерностях и порядках измеряемых величин, с которыми придется иметь дело при выполнении работы, а также о методе измерения и используемых приборах, последовательности действий при проведении измерений.
|
|
|
Для записей результатов работы надо подготовить рабочую тетрадь, лучше большого формата, чтобы ее можно было использовать в течение, по крайней мере, одного семестра. Оформление каждой работы нужно начинать с номера и названия. Далее должны быть представлены краткое изложение теории, схема установки и описание хода эксперимента.
Прежде чем приступить к выполнению работы, следует продумать предложенный в описании план действий, определить необходимое количество измерений. В соответствии с этим предварительно подготовить таблицы, в которые будут заноситься результаты.
Желательно заранее представлять диапазон изменения измеряемых величин и выбрать для них соответствующие единицы. В крайнем случае, это нужно сделать на начальном этапе работы. Необходимо подумать о точности измерений. Например, при косвенных измерениях величин, имеющих степенную зависимость от непосредственно измеряемых, относительная погрешность величин, входящих с большими показателями степени, должна быть меньше, то есть их следует измерять точнее. По возможности следует избегать методов, при которых приходится вычислять разность двух близких по значениям величин. Например, толщину стенки тонкой трубки лучше измерить, как отмечалось, непосредственно, а не вычислять по значениям внешнего и внутреннего диаметров.
Начало работы. В начале работы необходимо тщательно ознакомиться с экспериментальной установкой, проверить работоспособность приборов. Нужно хорошо разобраться, как они регулируются, включаются и выключаются.
Всегда очень важно аккуратное и бережное обращение с приборами. Не следует вскрывать чувствительные приборы и менять настройку.
Все сведения о приборах (в первую очередь класс точности, максимальное значение на шкале, по которой производятся измерения, и цену деления) и условиях эксперимента необходимо записать в рабочей тетради, так как они потребуются при получении окончательных результатов.
|
|
|
При составлении (собирании) электрических схем источники питания подключаются к схеме в последнюю очередь.
Прежде чем приступить к основным измерениям, необходимо проверить работу установки. Первые измерения должны быть контрольными, чтобы убедиться, что все работает нормально, диапазон и точность измерений выбраны правильно. Если разброс повторных измерений не превышает систематическую погрешность, то многократных измерений не требуется.
Замеченные неполадки в работе приборов и установок надо зафиксировать (делать соответствующую запись в тетради) и сообщить об этом преподавателю.
Проведение измерений. Все записи результатов измерений должны быть сделаны четко и подробно, с нужными пояснениями.
Полезно строить предварительные графики зависимостей измеряемых величин между собой или от изменения параметров по мере получения результатов. При этом сразу выделяются области резких изменений, в которых измерения должны проводиться подробнее (больше точек), чем на участках плавного изменения. Если изучаемая закономерность, например, линейность, выполняется только на некотором участке, то область измерений должна быть выбрана шире этого участка, чтобы можно было установить границы выполнения закономерности.
Если в начале работы выясняется, что разброс результатов измерений очень большой, то иногда лучше поискать и устранить причину этого, чем выполнять большое количество измерений для получения необходимой точности результата. При изучении зависимости измеряемой величины от параметра или другой измеряемой величины надо убедиться, что за время измерений в процессе работы не произошло никаких сбоев или существенных изменений внешних условий, влияющих на результаты, для чего в конце работы необходимо повторить начальные измерения либо проделать все измерения в обратном порядке.


 Перед каждой таблицей должны быть указаны значения цены деления и класс точности каждого прибора, которым производятся измерения. В таблицу необходимо заносить число делений, а не саму величину, например, тока или напряжения. Это убережет вас от ошибки при записи экспериментальных данных. В конечном счете это главное, так как обработка данных может быть проведена разными способами и в любое время, а измерения воспроизвести бывает трудно, а иногда и невозможно.
Перед каждой таблицей должны быть указаны значения цены деления и класс точности каждого прибора, которым производятся измерения. В таблицу необходимо заносить число делений, а не саму величину, например, тока или напряжения. Это убережет вас от ошибки при записи экспериментальных данных. В конечном счете это главное, так как обработка данных может быть проведена разными способами и в любое время, а измерения воспроизвести бывает трудно, а иногда и невозможно.
|
|
|
Единицы измерения надо выбирать так, чтобы результаты измерения представлялись числами в диапазоне примерно от 0,1 до 1000. При этом таблицы не будут громоздкими, а графики будут удобными для использования. Например, для модуля Юнга металлов (обозначаемых буквой Е), численные значения которых в системе СИ очень велики, в качестве единицы измерения берут 1010 Н/м2. Тогда наименование графы таблицы или оси графика будет выглядеть следующим образом: Е, 1010 Н·м -2. Запятая здесь играет важную роль — она отделяет обозначение величины, приводимой в таблице или откладываемой по оси координат, от единицы измерения. В графе таблицы для алюминия будет стоять 7,05, а на шкалах графиков — небольшие целые числа. Вместо множителя перед единицами измерения могут быть использованы также слова или их сокращения.
Иногда используется другой способ наименования. В таблицах или на осях графиков представляют не саму величину, а произведение ее на некоторый коэффициент, которое измеряют в обычных единицах. Для модуля Юнга при этом получаем: Е · 10 -10, Н·м -2. Хотя и в данном случае в таблице для алюминия будет стоять 7,05, этот способ меньше используется из-за возможных ошибок при переходе к значению Е, так как множитель по ошибке может быть отнесен к единицам измерения.
Расчеты, анализ и представление результатов. Полученные первичные результаты в виде таблиц и графиков используются для расчета конечных значений величин и их погрешностей либо для нахождения зависимости измеряемых величин между собой. Все расчеты удобно проводить в той же рабочей тетради, где записаны первичные результаты измерений, и заносить в соответствующие свободные колонки таблиц с экспериментальными данными. Это поможет проводить проверку, анализ и сопоставление получаемого результата с исходными данными.
|
|
|
Для измеряемых величин окончательные результаты должны быть представлены в виде среднего значения, погрешности и количества проведенных измерений. В случае косвенных измерений для получения окончательного результата используются их зависимости от измеряемых величин, по которым вычисляют и средние значения и погрешности.
Поскольку погрешность ошибки редко удается определить с точностью лучше 20%, при записи результата нужно округлять величину ошибки до одной -двух значащих цифр. Например, правильные записи погрешностей: ±3; ±0,2; ±0,08; ±0,14; неправильные записи: ±3,2; ±0,23; ±0,084. Величину ±0,14 не следует округлять до ±0,1, так как при этом округлении погрешность изменяется на 40%. При записи результата измерения последняя цифра значения физической величины должна быть того же разряда, что и в погрешности. Например, некоторый результат при погрешности ±0,012, записываемый 1,243 ±0,012, при большей погрешности (±0,03) принимает вид 1,24 ± 0,03, а при еще большей погрешности (0,2) — 1,2 ± 0,2. В промежуточных расчетах можно сохранить в числах лишнюю значащую цифру для лучшего округления конечного значения. В зависимости от выбора единиц измерения погрешность может составлять десятки, сотни, тысячи или более единиц измерения. Например, если вес тела определен с точностью до 0,5 кг и составляет 58,3 ± 0,5 кг, то его можно выразить и в граммах: (583 ± 5) · 102 г. Неправильно было бы написать: 58300 ± 500 г.
Для окончательной оценки качества полученных результатов измерений надо сравнить их с данными, приводимыми в справочниках.
Построение и обработка графиков. Для построения графиков следует использовать специальную бумагу: в клетку, миллиметровую, логарифмическую или полулогарифмическую. Размер графика (и соответственно формат листа бумаги) не должен быть очень малым или очень большим. Лучше если он будет иметь размер от четверти до полного листа рабочей тетради.
При построении графика, прежде чем наносить точки, нужно выбрать подходящий масштаб и начало отсчета на осях координат. Выбор должен быть таким, чтобы наносимые точки располагались на всей площади листа.
На рисунке 2 изображены примеры правильного и неправильного построения графика. На левом (неправильно построенном) графике экспериментальные точки занимают нижнюю правую часть рисунка. Чтобы этого избежать, следует выбрать более крупный масштаб по оси Y и сместить нуль на оси абсцисс, как это сделано на правом графике.
|
|
|
Обозначения функций и единиц измерения на осях координат должны быть ясными и четкими. Не обязательно наименовать все деления шкалы, но надо сделать столько надписей, чтобы ими было легко и удобно пользоваться. Писать их лучше на внешней стороне осей координат. Если используется бумага с сеткой, имеющей линии различной
толщины, то на жирных линиях следует располагать круглые значения величин. Удобно, если клеточка сетки соответствует 0,1; 0,2; 0,5; 1; 2; 5; 10 единицам масштаба измерения откладываемой по оси величины. Неудобно, если одной клетке соответствуют 2,5; 3; 4; 7 и тому подобное количество единиц масштаба. При неудобном масштабе нанесение точек на график и определение координат точек на графике требует большего времени и нередко сопровождается ошибками. Наименование величины, откладываемой по оси абсцисс, пишется снизу у конца оси, а по оси ординат — вверху слева. Через запятую указывается единица измерения.
Точки, наносимые на график, должны изображаться четко и ясно. Их следует наносить карандашом, чтобы можно было исправить при обнаружении ошибок. Не следует делать никаких загромождающих график больших пояснительных надписей или указывать около точек их числовые значения. Если пояснения необходимы, то точка или линия обозначается цифрой и в тексте или на полях графика делается соответствующее пояснение. Точки, полученные в различных условиях, например, при нагревании и охлаждении, при увеличении и уменьшении нагрузки и т. д., полезно наносить различными значками или цветами.
При нанесении на график экспериментальных точек, для которых известны погрешности, полезно указывать эти погрешности отрезками линий, величина которых соответствует величине погрешности по каждой из переменных, определяющих точку. В таком случае точка изображается крестом. Половина размера креста по горизонтали должна быть равна погрешности по оси абсцисс, а половина размера по вертикали — погрешности по оси ординат. В том случае, если одна из погрешностей - из-за своей малости — не может быть изображена графически, результаты изображаются черточками, вытянутыми на ±  в том направлении, где погрешность не мала. Такое изображение экспериментальных точек облегчает анализ результатов, в частности, поиск зависимостей, наилучшим способом их описывающих, сравнение с теоретическими расчетами или результатами других исследований.
в том направлении, где погрешность не мала. Такое изображение экспериментальных точек облегчает анализ результатов, в частности, поиск зависимостей, наилучшим способом их описывающих, сравнение с теоретическими расчетами или результатами других исследований.
На рисунке 3а, б, на которых изображены одни и те же экспериментальные точки при разных погрешностях измерений, график 3а, несомненно, указывает на нерегулярный ход изучаемой зависимости. Эта зависимость изображена на рисунке кривой линией. Те же данные при больших погрешностях опыта (рисунок 3б) с успехом описываются прямой линией, так как только одно измерение отступает от этой прямой больше, чем на стандартную погрешность (и меньше, чем на две такие погрешности). То обстоятельство, что данные на рисунке 3а требуют  проведения кривой линии, а на рисунке 3б не требуют, проясняется лишь при изображении результатов в виде креста погрешностей.
проведения кривой линии, а на рисунке 3б не требуют, проясняется лишь при изображении результатов в виде креста погрешностей.
Часто измерения проводятся с целью получения или подтверждения зависимостей между измеряемыми величинами. В этих случаях необходимо по экспериментальным точкам провести соответствующую зависимость и, если нужно, найти погрешности измеряемых величин по разбросу экспериментальных точек. Легче всего по экспериментальным точкам проводить прямую линию. Поэтому если из теории или некоторых предположений известна возможная зависимость между измеряемыми величинами, то по осям координат надо отложить такие функции измеряемых величин, которые лучше соответствуют линейной зависимости. Например, при исследовании зависимости времени падения тела в поле тяжести от высоты, с которой оно падает, по осям нужно отложить высоту и квадрат времени, так как в однородном поле тяжести без учета сопротивления воздуха квадрат времени падения пропорционален высоте падения. Это особенно удобно, если требуется определить еще и ускорение падения. Менее удобным было бы откладывание по осям времени и корня квадратного из высоты, хотя и в этом случае зависимость также линейна. Отметим, что линейная зависимость должна получиться и при откладывании по осям координат логарифмов времени и высоты. Но логарифмический масштаб в данном случае плох тем, что линейность сильно нарушается при небольших погрешностях в начале отсчета времени и высоты. Логарифмический масштаб удобен в случае степенных зависимостей и больших диапазонов изменения переменных. Получающиеся линейные зависимости позволяют по графику найти показатель степенной зависимости.
Существуют различные методы проведения прямых линий через экспериментальные точки. Самый простой способ, пригодный для оценки результатов, но не для получения окончательного значения, состоит в использовании прозрачной линейки или прозрачного листа с нарисованной на нем прямой линией. Благодаря прозрачности линейки видно, сколько точек находится по обе стороны от проводимой линии. Ее надо провести так, чтобы по обе стороны было одинаковое количество экспериментальных точек. Параметры этой линии (наклон, пересечения с осями координат) измеряются непосредственно на графике. В результате получаем аналитическое выражение прямой  , которая в общем случае при а, не равном нулю, не проходит через начало координат.
, которая в общем случае при а, не равном нулю, не проходит через начало координат.
Случайные погрешности определения а и b можно оценить по графику следующим образом. Для оценки погрешности а находим величины, на которые надо параллельно сместить линию, чтобы число точек по обе стороны относилось, как 1: 2 (рисунок 4). То есть при смещении линии

вверх по у на  выше линии находится в два раза меньше точек, чем ниже ее, а при смещении вниз на
выше линии находится в два раза меньше точек, чем ниже ее, а при смещении вниз на  ниже ее находится в два раза меньше точек, чем выше. Если всего экспериментальных точек
ниже ее находится в два раза меньше точек, чем выше. Если всего экспериментальных точек  , то для оценки погрешности а имеем
, то для оценки погрешности а имеем
 .
.
Для оценки погрешности коэффициента b надо диапазон изменения координаты х экспериментальных точек разделить на три равные части и поворачивать линию таким образом, чтобы в крайних частях соотношения числа точек на разных сторонах линии было 1: 2 (рисунок 5).

|


 То есть увеличиваем наклон линии до значения
То есть увеличиваем наклон линии до значения  так, чтобы в левом крайнем участке над линией оказалось в два раза больше экспериментальных точек, чем под ней, а в правом крайнем участке под линией оказалось в два раза точек больше, чем над ней. Затем уменьшаем наклон линии до
так, чтобы в левом крайнем участке над линией оказалось в два раза больше экспериментальных точек, чем под ней, а в правом крайнем участке под линией оказалось в два раза точек больше, чем над ней. Затем уменьшаем наклон линии до  так, чтобы в левом крайнем участке под линией было в два раза больше точек, чем над ней, а в правом участке было под линией в два раза меньше точек, чем над ней. Для оценки погрешности
так, чтобы в левом крайнем участке под линией было в два раза больше точек, чем над ней, а в правом участке было под линией в два раза меньше точек, чем над ней. Для оценки погрешности  имеем
имеем
 .
.
В случае зависимости  , проходящей через начало координат, для оценки погрешности коэффициента
, проходящей через начало координат, для оценки погрешности коэффициента  также надо диапазон изменения координаты х разбить на три равные части. Точки в ближайшей к началу координат части не учитываются. Определяется
также надо диапазон изменения координаты х разбить на три равные части. Точки в ближайшей к началу координат части не учитываются. Определяется  ,при котором над линией находится точек в два раза меньше, чем под ней (из всех точек в средней и правой частях), и
,при котором над линией находится точек в два раза меньше, чем под ней (из всех точек в средней и правой частях), и  , при котором соотношение числа точек над и под линией противоположное. Для оценки погрешности
, при котором соотношение числа точек над и под линией противоположное. Для оценки погрешности  имеем
имеем
 .
.
Более точным и обоснованным методом проведения прямой линии по точкам является метод наименьших квадратов, который основан на минимизации суммы квадратов отклонений точек от прямой. Это означает, что коэффициенты а и b в линейной зависимости  находятся из условия минимума функции
находятся из условия минимума функции

 . (26)
. (26)
Здесь  и
и 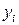 — координаты экспериментальных точек.
— координаты экспериментальных точек.
Приведем окончательные формулы для а и b и их погрешностей через средние значения  и
и 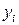 :
:
 , (27)
, (27)
 . (28)
. (28)
Погрешности этих коэффициентов соответственно равны:
 , (29)
, (29)
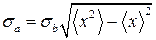 . (30)
. (30)
Если известно, что точки должны описываться линейной зависимостью у = kх, проходящей через начало координат, то для коэффициента k и погрешности его определения получаем
 , (31)
, (31)
 . (32)
. (32)
Этот метод довольно трудоемкий, но при наличии калькулятора или компьютера он является наиболее предпочтительным.
Бывают случаи, когда по экспериментальным точкам не надо находить описывающую их зависимость, а требуется определить лишь численное значение функции для переменной, лежащей где-то между экспериментальными точками. В таких случаях используются интерполяционные методы. В простейшем случае предполагается линейная зависимость между соседними точками и используются значения в этих точках. Для интерполяции по параболе (метод Симпсона) требуются значения в трех точках.
Еще раз подчеркнем, что графики необходимы для наглядного представления результатов измерений. Они очень удобны для сравнения результатов экспериментов и теорий, выяснения качественных особенностей зависимостей, быстрых оценок характера изменения величин на отдельных участках. Однако документом эксперимента является таблица с экспериментальными данными.
Как правило, результаты опытов получаются из экспериментальных данных путем вычисления. Вычисления следует проводить не точнее, чем это необходимо в данном конкретном случае. Большую помощь при расчетах оказывают формулы для приближенных вычислений, позволяющих во многих случаях значительно упростить расчеты. В таблице 1 приводится ряд таких формул. В последних графах таблицы приводятся значения переменных, для которых написанные приближенные формулы обеспечивают указанную в заголовке графы точность.
Отметим, что наши рекомендации по обработке результатов эксперимента не претендуют ни на полноту, ни на особую строгость, так как рассчитаны на студентов 1-го курса, чья математическая подготовка недостаточна для строгого рассмотрения всех вопросов, связанных с математической статистикой. Более глубокое изложение станет возможным лишь после первых двух курсов обучения, когда накопится достаточный опыт экспериментальной работы и будет освоен соответствующий математический аппарат. Поэтому часть формул, применяемых
для обработки экспериментальных результатов измерений, была приведена без вывода. Напомним о некоторых из них, включив в сводку основных формул (таблица 2).
В заключение дадим несколько рекомендаций по обработке результатов измерений.
При обработке результатов следует тщательно обдумывать возможные источники ошибок. Промежуточные вычисления должны выполняться с точностью, несколько превосходящей точность измерений, чтобы избежать влияния неоправданных ошибок, связанных с вычислениями. При вычислениях обычно сохраняют на один знак больше, чем будет оставлено в окончательном ответе.
| Формула | Точность 5% | Точность 1% | Точность 0,1% |


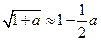





|  меньше
0,22
0,63
0,36
0,31
0,10
0,55
0,4
0,8 меньше
0,22
0,63
0,36
0,31
0,10
0,55
0,4
0,8
|  меньше
0,1
0,28
0,16
0,14
0,02
0,24
0,17
0,34 меньше
0,1
0,28
0,16
0,14
0,02
0,24
0,17
0,34
|  меньше
0,032
0,09
0,052
0,045
0,002
0,077
0,055
0,11 меньше
0,032
0,09
0,052
0,045
0,002
0,077
0,055
0,11
|



|
Таблица 1 – Некоторые формулы приближенных вычислений
Таблица 2 – Сводка основных формул
| Наилучшее значение измеряемой величины | 
|
| Оценка погрешности среднего значения измеряемой величины | 
|
| Сложение погрешностей (независимых) | 
|
| Погрешность результата расчета |  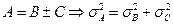
  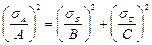

|
| Допустимые масштабы | 1:1; 1:2; 1:5; 1:10; 1:20… 2:1; 5:1; 10:1; 20:1… |
Проведение наилучшей прямой 
| 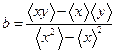 , , 
|
Проведение наилучшей прямой 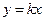
| 
|
СПИСОК ЛИТЕРАТУРЫ
1. Лабораторные занятия по физике / Под ред. Л.Л. Гольдина. — М.: Наука,
1983.
2. Лабораторный практикум по общей физике. Т. 3 / Под ред. Ю.М. Ципеню-
ка. — М.: Изд-во МФТИ, 1998.
3. Сквайре Дж. Практическая физика. — М.: Мир, 1971.
|
|
|
12 |


