 |
Информационное обеспечение
|
|
|
|
Пояснительная записка
Учебной дисциплиной "Математика" предусматривается формирования у студентов представлений о математике как универсальном языке науке; развития логического мышления, пространственного воображения, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования.
Контрольные задания составлены на основе рабочей программы по математике по специальностям среднего профессионального образования.
По данной дисциплине предусматривается выполнение одной домашней контрольной работы, охватывающей все разделы учебной программы.
На установочных занятиях студентов знакомят с программой дисциплины, методикой работы над материалом и выполнения домашней контрольной работы.
Выполнение контрольной работы определяет степень усвоения студентами изучаемого материала и умения применять полученные знания при решении практических задач.
Проведение практических занятий предусматривает своей целью закрепление теоретических знаний и приобретение практических умений по программе учебной дисциплины.
В результате изучения учебной дисциплины студент должен:
уметь: выполнять необходимые измерения и связанные с ними расчеты; вычислять площади и объемы деталей строительных конструкций, объемы земляных работ; применять математические методы для решения профессиональных задач;
знать: основные понятия о математическом синтезе и анализе, дискретной математики, теории вероятности и математической статистики; основные формулы для вычисления площадей фигур и объемов тел, используемых в строительстве.
ТЕМАТИЧЕСКИЙ ПЛАН И СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
|
|
|
| Наименование разделов и тем | Содержание учебного материала |
| Раздел 1. Дифференциальные и интегральное исчисления | |
| Тема 1.1. Функция. Предел функции в точке | Функция. Свойства функции. Предел функции в точке |
| Тема 1.2. Производная и дифференциальная функции. Приложение производной к исследованию функции | Производная функции в точке. Правила и формулы дифференцирования. Применение производной к исследованию функций |
| Тема 1.3. Интеграл и его приложения | Неопределенный интеграл, его свойства. Таблица неопределенных интегралов. Определенный интеграл, его свойства. Вычисление определённого интеграла |
| Тема 1.4. Дифференциальные уравнения | Дифференциальные уравнения I порядка. Дифференциальные уравнения II порядка |
| Раздел 2. Элементы теории вероятностей и математической статистики | |
| Тема 2.1. Элементы теории вероятности | Элементы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей. Случайный опыт. Случайное событие. Закон распределения случайной величины. Числовые характеристики случайной величины |
ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
| Наименование практических работ | |
| Тема 1.2. | Вычисление производных функции. Исследование и построение графиков функции с помощью производной |
| Тема 1.3. | Методы интегрирования. Приложение определенного интеграла к вычислению площадей плоских фигур |
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ
И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ЕЕ ВЫПОЛНЕНИЮ
Учебный план по математике предполагает выполнение студентами одной контрольной работы и дифференцированного зачёта по предмету.
Содержание контрольной работы приведено в десяти вариантах. Номер варианта определяется последней цифрой учебного шифра студента, если шифр заканчивается нулем, то выполняется десятый вариант.
|
|
|
Работа должна быть выполнена в отдельной тетради чернилами (черными или синими). Условие заданий записываются полностью. Решение должно быть подробным и сопровождаться краткими пояснениями. Завершается решение ответом, в котором при необходимости ответ комментируется.
Для пометок и замечаний преподавателя необходимо оставлять поля шириной 40 мм и соблюдать достаточный интервал между строчками. Тексты заданий переписывать обязательно. В конце контрольной работы должна быть указана литература, использованная при ее выполнении, дата окончания работы и личная подпись студента.
Контрольная работа должна быть выполнена в сроки, указанные в индивидуальном учебном графике. К сдаче экзамена допускаются студенты, имеющие зачет по домашней контрольной работе.
После получения прорецензированной работы студенту необходимо исправить отмеченные ошибки, выполнить все указания преподавателя, повторить недостаточно усвоенный материал.
Не зачтенные контрольные работы подлежат повторному выполнению.
Контрольная работа
Вариант 1
1. Вычислите пределы:
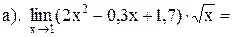
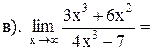
2. Найдите производную функции: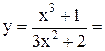 
3. Вычислите ускорение движущейся материальной точки в момент времени t=4c, если скорость определяется формулой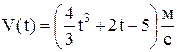 
4. Найдите неопределённый интеграл: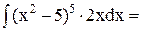 
5. Вычислите площадь фигуры, ограниченной линиями 
; 
; 
; 
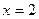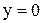
6. Решите дифференциальное уравнение: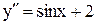 
7. Составьте уравнение кривой, проходящей через точку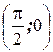 
, если угловой коэффициент касательной к ней в любой точке определяется по формуле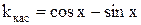 
8. Сколькими способами можно назначить двух дежурных из 30 студентов?
9. Какова вероятность того, что при бросании игрального кубика на его верхней грани выпадает четное число очков?
Вариант 2
1. Вычислите пределы:
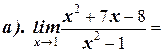
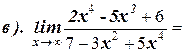
2. Найдите производную функции: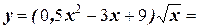 
3. Найдите формулу мгновенной угловой скорости w, если закон вращения тела вокруг своей оси задается формулой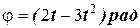 
4. Найдите неопределённый интеграл: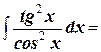 
5. Вычислите объем тела, полученного от вращения вокруг оси 0х криволинейной трапеции, ограниченной линиями: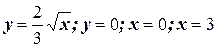 
6. Решите дифференциальное уравнение: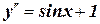 
7. Составьте закон движения материальной точки, если скорость его движения определяется формулой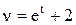 
и 
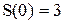, где t в секундах, 
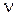в 
и S в м.
|
|
|
8. Имеется две путёвки в один санаторий. Сколькими способами их можно распределить между пятью претендентами?
9. Студент знает 50 вопросов из 60. Какова вероятность того, что он знает ответ на два вопроса, предложенных ему на экзамене?
Вариант 3
1. Вычислите пределы:
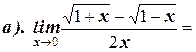
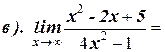
2. Найдите производную функции: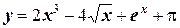 
3. Тело вращается по закону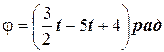 
. Найдите угловую скорость вращения w в момент времени t = 2с.
4. Найдите неопределённый интеграл: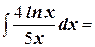 
5. Вычислите работу, которую надо совершить, чтобы растянуть пружину на 2 см, если коэффициент упругости материала пружины 2200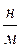 
6. Решите дифференциальное уравнение: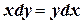 
7. Тело вращается вокруг оси с угловой скоростью 
. Составьте закон движения 
, если 
.
8. Сколько трёхзначных чисел можно составить из цифр 1; 3; 5; 7; 9, без повторения цифр в числе?
9. На сто билетов в денежно-вещевой лотерее приходится 1 денежный и 9 вещевых выигрышей. Какова вероятность того, что наудачу взятый билет выигрышный?
Вариант 4
1. Вычислите пределы:
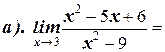
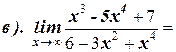
2. Найдите производную функции: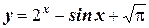 
3. Вычислите угловой коэффициент касательной к параболе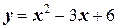 
в точке, абсцисса которой равна 4.
4. Найдите неопределённый интеграл: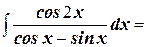 
5. Вычислите работу, которую надо совершить, чтобы растянуть пружину длиной 0,5 м до 0,55 м, если коэффициент упругости материала пружины 2000 .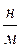
6. Решите дифференциальное уравнение: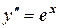 
7. Составьте уравнение функции, график которой проходит через точку М0 (0;5) и производная функции задана формулой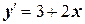 
8. Сколько трёхцветных флагов можно раскрасить тремя цветными карандашами, располагая полосы горизонтально?
9. Одновременно бросают два игральных кубика. Какова вероятность того, что сумма очков на верхних гранях равна 9?
Вариант 5
1. Вычислите пределы:
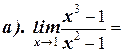
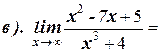
2. Найдите производную функции: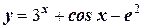 
3. Материальная точка движения по закону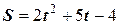 
. Найдите ускорение движения.
4. Найдите неопределённый интеграл: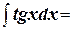 
5. Вычислите площадь фигуры, ограниченной линиями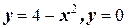 
6. Решите дифференциальное уравнение: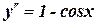 
|
|
|
7. График функции проходит через точку (0;3), а её производная задана уравнением 
. Составьте уравнение этой кривой.
8. Сколько способов расставить 7 учебников на полке, чтобы 2 учебника по математике были рядом?
9. Из колоды карт (36 листов) выбирают одну. Какова вероятность того, что вынули даму?
Вариант 6
1. Вычислите пределы:
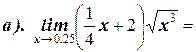
2. Найдите производную функции: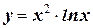 
3. Вычислите ускорение движущейся материальной точки в момент времени 
, если скорость движения задана формулой: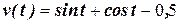 
.
4. Найдите неопределённый интеграл: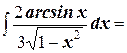 
5. Вычислите площадь фигуры, ограниченной линиями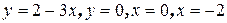 
6. Решите дифференциальное уравнение: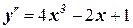 
7. Составьте уравнение кривой, проходящей через точку (p;5), если угловой коэффициент касательной к ней в любой точке определяется по формуле 
.
8. Сколько вариантов выбора старосты и физорга из 30 студентов?
9. Какова вероятность того, что из полного набора домино (28 пластинок) взяли дубль?
Вариант 7
1. Вычислите пределы:
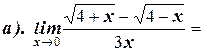
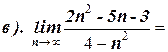
2. Найдите производную функции: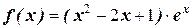 
3. Исследуйте функцию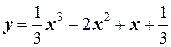 
на выпуклость, вогнутость и точку перегиба.
4. Найдите неопределённый интеграл: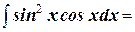 
5. Вычислите объем тела полученного от вращения криволинейной трапеции, ограниченной линиями: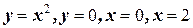 
, вокруг оси Ох.
6. Решите дифференциальное уравнение: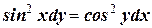 
7. Материальная точка движется со скоростью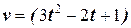 
. Составьте закон движения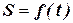 
, если начальный путь равен 0.
8. Имеются две путёвки в разные санатории. Сколькими способами их можно распределить между пятью претендентами?
9. В ящике 10 деталей, из них две нестандартные. Какова вероятность того, что среди трёх, наудачу взятых деталей, нестандартных не будет?
Вариант 8
1. Вычислите пределы:
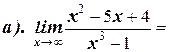
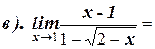
2. Найдите производную функции: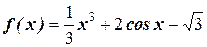 
3. Тело вращается вокруг своей оси по закону 
. Вычислите угловую скорость вращения w в момент времени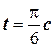 
.
4. Найдите неопределённый интеграл: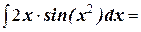 
5. Вычислите работу, которую совершает сила в 60 Н, растягивающая пружину на 0,02 м.
6. Решите дифференциальное уравнение: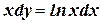 
.
7. Тело вращается вокруг своей оси с угловой скоростью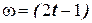 
. Составьте закон вращения, если .
8. Сколько двузначных чисел можно составить из цифр 2, 4, 6, 8?
9. Какова вероятность правильно набрать номер телефона, если вы забыли последнюю цифру?
Вариант 9
1. Вычислите пределы:
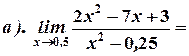
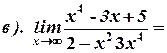
2. Найдите производную функции: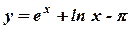 
3. Исследуйте функцию 
на монотонность.
4. Найдите неопределённый интеграл: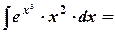 
5. Вычислите силу давления воды на прямоугольную пластинку, длина которой равна 2 м, ширина 0,5м, расположенную вертикально, большей стороной параллельно поверхности воды, верхний край которой находится на глубине 1,5 м, если плотность воды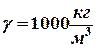 
, ускорение свободного падения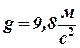 
|
|
|
6. Решите дифференциальное уравнение: 
7. Составьте уравнение функции, график которой проходит через точку (0;3), угловой коэффициент касательной в любой точке графика задан уравнением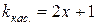 
8. Сколько способов расставить 7 книг на полке?
9. Какова вероятность того, что четырёхтомное собрание сочинений А.С. Макаренко стоит на полке по порядку?
Вариант 10
1. Вычислите пределы:
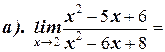
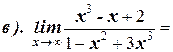
2. Найдите производную функции: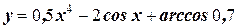 
3. Вычислите максимум и минимум функции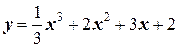 
4. Найдите неопределённый интеграл: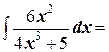 
5. Вычислите площадь фигуры, ограниченной линиями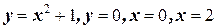 
6. Решите дифференциальное уравнение: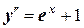 
7. Составьте уравнение кривой, проходящей через точку (1;5), угловой коэффициент касательной которой в любой точке задан уравнением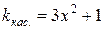 
8. Сколько трёхзначных номеров для автомашин можно составить из 10 цифр, без повторения цифр?
9. В урне 7 белых, 5 красных и 8 чёрных шаров. Какова вероятность того, что вынутый шар белый?
ВОПРОСЫ К ЗАЧЁТУ
1. Что называется числовой функцией?
2. Что называется последовательностью?
3. Какая функция называется монотонной?
4. Какая функция называется периодической?
5. Какая функция называется чётной или нечётной?
6. Какая функция называется обратной заданной функции?
7. Какая функция называется сложной?
8. Что называется пределом функции в точке?
9. Что называется пределом последовательности?
10. Какая функция называется непрерывной в точке, на (а; в), на [а; в]?
11. Что такое точка разрыва? Их виды (по графику)
12. Что называется производной функции в точке? Её геометрический и механический смысл.
13. Что называется первообразной? Неопределенным интегралом? Его свойства.
14. Уметь читать формулы табличных производных и интегралов, применять их для решения задач.
15. Что называется определенным интегралом? Его свойства.
16. Вычисление площади криволинейной трапеции с помощью определенного интеграла.
17. Применение определенного интеграла для решения геометрических и физических задач.
18. Какое уравнение называется дифференциальным? Его порядком? Решением: общим, частным, особым.
19. Решение дифференциального уравнение с разделяющимися (разделенными) переменными I порядка.
20. Решение дифференциальных уравнений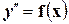 
, где 
- многочлен, показательная функция или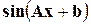 
.
21. Какое уравнение называется дифференциальным однородным, линейным II порядка с постоянными коэффициентами и три случая его решения.
22. Что называется размещением 
- перестановками, сочетанием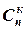 
, формулы для подсчета их количества.
23. Что называется случайным событием, их виды?
24. Относительная частота и вероятность случайного события.
25. Определение суммы событий и теоремы о сложении вероятностей.
26. Определение произведения событий и теорема об умножении вероятностей.
27. Формула полной вероятности.
28. Формула Бернулли.
29. Случайная величина, закон её распределения.
30. Характеристики случайной величины: математическое ожидание, дисперсия, их свойства.
ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ
Основные источники:
1. В.С. Щипачев. «Основы высшей математики» – М.: «Высшая школа» 2012 г.
2. П.Е. Данко, А.Г. Попов «Высшая математика в упражнениях и задачах» ч.I,II - М.: «Высшая школа» 2011 г.
3. Г.И. Москинова «Дискретная математика» М.: «Логос» 2012 г.
4. Н.В. Боголюбов «Практические занятия по математике» - М.: «Высшая школа» 2011 г.
5. В.Е. Гмурман «Руководство к решению задач по теории вероятности и математической статистике» - Москва, Форум. ИНФРА-И, 2011 г.
6. В.Е. Гмурман «Теория вероятности и математическая статистика» - Москва, 2011 г.
Дополнительные источники:
1. Е.С. Кочетков, С.О. Смерчинская, В.В. Соколов «Теория вероятностей и математическая статистика» М.: «Форум» «ИНФРА-И», 2010 г.
2. А.А.Дадоян «Математика» - М. «Форум» «ИНФРА», 2011 г.
3. И.И. Валуцэ «Математика для техникумов» - М. «Наука», 2010 г.
4. В.Е. Гмурман «Руководство к решению задач по теории вероятности и математической статистике» - Москва, «Форум». «ИНФРА-И», 2010 г.
5. Н.В. Богомолов «Практические занятия по математике». М.: «Высшая школа», 2011 г.
Интернет-ресурсы:
1. http//www.pm298.ru – Математика: справочник формул по алгебре и геометрии.
2. http://www. mathtest.ru – Математика в помощь школьнику и студенту.
3. http://www.klyaksa.net
4. http://infoschool.narod.ru/
|
|
|
