Функция, заданная неявно, и ее производная

Производная по направлению, градиент ФНП

Применим теперь правила вычисления производных сложных функций нескольких переменных для вычисления производных по направлению.

Прежде всего разберемся, что такое направление. Допустим, что мы находимся на плоскости. Проведем вектор единичной длины, исходящий из начала координат. Его определяет угол от оси абсцисс до радиус-вектора и общий вид такого вектора - . К любой точке 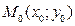прикладываем этот вектор и тем самым указываем направление движения. В какую точку мы попадем, если из точки 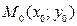продвинемся в направлении на расстояние ? Это будет точка . Теперь естественным будет определение производной функции двух переменных по направлению.

Определение 14. Пусть задана функция , точка 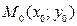и направление . Предел , (5) если этот предел существует, называется производной функции по направлению в точке 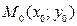и обозначается .

Геометрически понятней будет запись предела в виде . Если функция дифференцируема, то справедливо соотношение и формула (5) преобразуется к виду . (6) Также будет верна запись . В обоих случаях правую часть формул можно представить в виде скалярного произведения вектора, составленного из частных производных функции в этой точке на единичный вектор направления. Теперь естественным выглядит следующее определение.

Определение 15. Вектор, составленный из частных производных функции нескольких переменных в точке, называется градиентом ФНП в этой точке и обозначается .

Итак, для функции двух переменных . (7)

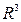Рассмотрим теперь случай функции трех переменных в пространстве . Проведем вектор единичной длины, исходящий из начала координат. Пусть у этого вектора угол с осью абсцисс равен , угол с осью ординат равен , угол с осью аппликат равен . Заметим, что при этом вектор направления записывается в виде и обязательно выполнено условие , т. к. длина этого вектора равна 1. Аналогично к любой точке прикладываем этот вектор и тем самым указываем направление движения. Если из точки продвинемся в направлении на расстояние , то окажемся в точке . Производная по направлению функции трех переменных может быть снова представлена в виде или записано в развернутом виде . (8)

Также справедливо равенство . Градиент функции (9) также может быть использован для вычисления производной по направлению.

Отметим факты, верные для функций любого числа переменных. Пусть задана функция или , точка или и направление, определяемой вектором единичной длины , где 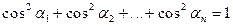. Производная по направлению также определяется формулой , где переменной является точка . Вектор из частных производных функции в точке , т. е. вектор-градиент помогает нам получить простую формулу для производной по направлению (10) или развернуто .

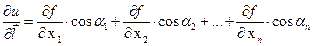Формула (10) показывает, что производная ФНП по направлению равна скалярному произведению градиента этой функции в данной точке на единичный вектор данного направления, т. е. равна произведению длины градиента на косинус угла между вектором градиента и единичным вектором направления. Следовательно, при изменении направления наибольшее значение производной по направлению будем в том случае, когда это направление совпадает с направлением градиента. В этом случае . Наименьшее значение производной по направлению будем в том случае, когда это направление противоположно направлению градиента. В этом случае . Если направление перпендикулярно направлению градиента, то значение производной по направлению равно 0.

Функция, заданная неявно, и ее производная

С уравнениями вида . (11) мы уже встречались. Например, это было уравнение эллипса (12) с положительными полуосями и . Эллипс образуют пары точек на плоскости с координатами , координаты которых удовлетворяют уравнению (12). Тем самым формируется зависимость одной из переменных, скажем от другой переменной, в данном случае . Порождает ли такое соответствие функцию 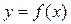? Ситуация здесь неоднозначная. Для того же эллипса (12) каждому соответствуют 2 значения второй переменной . Тем не менее в окрестности любой точки эллипса с ординатой, не равной 0, существует искомая функция или , которая содержит точки эллипса из окрестности такой точки. Множество точек на плоскости или просто пар таких чисел, удовлетворяющих (11), может быть пустым, например для мнимого эллипса 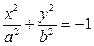. Оно может состоять из одной точки, например, для вырожденного эллипса это точка . Нам надо разобраться в этом вопросе и выяснить, при каких условиях и в какой области уравнение (11) равносильно функции .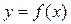

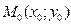Теорема 3. Пусть для дифференцируемой функции существует точка , координаты которой удовлетворяют уравнению (11), причем выполнено условие . Тогда существует функция 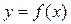, определенная в некоторой окрестности точки , обладающая тем свойством, что 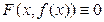в этой окрестности.

Доказательство. В силу дифференцируемости функции в окрестности точки 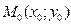справедливо равенство . Если величина отлична от 0, то можно на нее поделить полученное равенство и получить соотношение 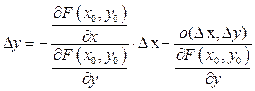. (13) Отсюда видно, что каждому приращению однозначно соответствует приращение . Это однозначно определяет функцию 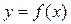, т. к. по условию теоремы точка 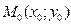уже удовлетворяет условию (11). Теорема доказана.

Следствие. Если в (13) поделить обе части на и перейти к пределу при , то мы получим формулу для вычисления производной функции, заданной неявно формулой (11): .