Гиперболический параболоид.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего образования

«Ижевский государственный технический университет им. М.Т. Калашникова»

(ФГБОУ ВО «ИжГТУ имени М.Т. Калашникова»)

Чайковский технологический институт (филиал) Федерального государственного бюджетного образовательного учреждения высшего образования

«Ижевский государственный технический университет им. М.Т. Калашникова»

(ЧТИ (филиал) ФГБОУ ВО «ИжГТУ имени М.Т. Калашникова»)

 

 

Кафедра «Промышленные технологии»

 

 

Работа защищена с оценкой

«______________________»

«___»______________20__г.

____________/____________

                                                                                                          

Реферат

по дисциплине «Линейная алгебра»

на тему «Поверхности второго порядка»

Выполнил:
Студент гр. Э-18/3,5з	М.В.Бусыгин
дата, подпись
Проверил:
к.т.н., доцент	Зверева Н.В.

Рецензия:

Степень достижения поставленной цели работы____________________________________

 

Полнота разработки темы _______________________________________________________

 

Уровень самостоятельности работы обучающегося__________________________________

_____________________________________________________________________________

Недостатки работы_____________________________________________________________

 

 

Чайковский, 2019

Содержание

Введение

Поверхности второго порядка

Понятие поверхности второго порядка.

Эллипсоид.

Однополосный гиперболоид.

Двуполостный гиперболоид.

Эллиптический параболоид.

Гиперболический параболоид.

Конус второго порядка.

Список литературы.

 

Введение

Чтобы заключить обзор развития и успехов новейшей геометрии, нам остается рассмотреть еще одну из отдельных теорий, наиболее важную и разработанную, именно теорию поверхностей второго порядка. Древние знали из поверхностей второго порядка кажется только конус, цилиндр и поверхности вращения, которые они называли сфероидами и коноидами. до Эйлера не усматривалось никакой другой аналогии между формами в пространстве и столь знаменитыми плоскими кривыми, названными коническими сечениями. Этот великий геометр распространил на кривые поверхности аналитический прием, служивший ему для исследования кривых линий на плоскости и открыл в общем уравнении второй степени с тремя обыкновенными координатами пять различных видов поверхностей, между которыми сфероиды и коноиды древних являются не более как частными формами.

Эйлер ограничился только этою классификациею. Но этого было достаточно, чтобы открыть геометрам обширное поле исследований, представляемых теориею поверхностей второго порядка.

 

Поверхности второго порядка

 1. Понятие поверхности второго порядка.

 

Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

a ₁₁ х² + а₂₂у² + a ₃₃z²+ 2 a ₁₂ xy + 2 a ₂₃ уz + 2 a ₁₃ xz + 2а ₁₄ x + 2а ₂₄ у+2а ₃₄ z +а ₄₄ = 0 (1)

в котором по крайней мере один из коэффициентов a ₁₁ , а₂₂, a₃₃ , a ₁₂ , a _23, a ₁₃ отличен от нуля.

Уравнение (1) мы будем называть общим уравнением по­верхности второго порядка. Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной де­картовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравне­ние (1) и уравнение, полученное после преобразования коор­динат, алгебраически эквивалентны.

 

Эллипсоид.

Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением:             

                                 (1)

 

Уравнение (1) называется каноническим уравнением эллипсоида.

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z = h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями

                                              (2)

Исследуем уравнения (2) при различных значениях h.

1) Если > c (c>0), то  и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z = h с данным эллипсоидом не существует.

2) Если , то  и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c) (плоскости  касаются эллипсоида).

3) Если , то уравнения (2) можно представить в виде

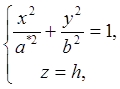
откуда следует, что плоскость z = h пересекает эллипсоид по эллипсу с полуосями  и . При уменьшении  значения и увеличиваются и достигают своих наибольших значений при , т. е. в сечении эллипсоида координатной плоскостью Oxy получается самый большой эллипс с полуосями  и .

Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz.

Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосями эллипсоида. В случае a = b = c эллипсоид является сферой.

Однополосный гиперболоид.

   Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

                   (3)

 

Уравнение (3) называется каноническим уравнением однополосного гиперболоида.

Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y =0) и Oyx (x =0). Получаем соответственно уравнения

                            и 

 

 

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями

                 или (4)

из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями   и ,

достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании  величины a* и b* возрастают бесконечно.

Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy.

Величины a, b, c называются полуосями однополосного гиперболоида.

 

Двуполостный гиперболоид.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

                      (5)

 

Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.

Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения

                          и

из которых следует, что в сечениях получаются гиперболы.

Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями

                            или           (6)

из которых следует, что при >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и . При увеличении  величины a* и b* тоже увеличиваются.

При   уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с) (плоскости  касаются данной поверхности).

При  уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом не существует.

Величина a, b и c называются полуосями двуполостного гиперболоида.

 

Эллиптический параболоид.

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

(7)

где p>0 и q>0.

Уравнение (7) называется каноническим уравнением эллиптического параболоида.

Рассмотрим сечения данной поверхности координатными плоскостями  Oxy и Oyz. Получаем соответственно уравнения

                                       и

из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат.

Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями

                               или          (8)

из которых следует, что при  плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями  и . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет.

Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши.

Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.

В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения).

 

Гиперболический параболоид.

Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением

  (9)           

где p>0, q>0.

Уравнение (9) называется каноническим уравнением гиперболического параболоида.

Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение

 

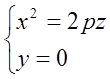                                          (10)

из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.

                                     

рассмотрим сечение данного параболоида плоскостью Oyz (x=0).

Получаем уравнение

                                          

из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения

                               

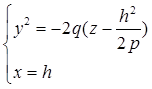
из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10).

Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy. получим уравнения

                     или

из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых

                          и

точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами.

 

Конус второго порядка.

Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

                      (11)

Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию

                            

распадающуюся на две пересекающиеся прямые

                       и

Аналогично, в сечении конуса плоскостью Oyz (x=0) также получаются две пересекающиеся прямые

                                               и

Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим

                                    или

из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями   . При увеличении абсолютной величины h полуоси a* и b* также увеличиваются.

При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).

 

Список литературы.

1. Канатиков А.Н., Крищенко А.П. Аналитическая геометрия: Учеб. для вузов. 2-е изд. / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000 – 388с.(Сер. Математика в техническом университете; Вып.III).

2. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.

3. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.

4. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: "Наука", 1988.

 

Поделиться:

Воспользуйтесь поиском по сайту: