 |
шаг – формирование третьего столбца.
|
|
|
|
Решение систем линейных алгебраических уравнений
Общий вид системы линейных алгебраических уравнений (СЛАУ)
Система 
линейных алгебраических уравнений с 
неизвестными записывается в виде:
где
– коэффициент 
-го 
уравнения системы при неизвестном 
для всех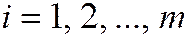 
и 
;
– неизвестные;
– свободные члены.
Таблица коэффициентов при неизвестных называется матрицей системы:
;
столбец 
– столбцом неизвестных;
столбец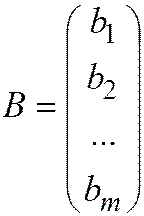 
– столбцом свободных членов.
Если матрица системы A – квадратная, то ее определитель обозначается чаще всего через 
и называется определителем системы.
Основными методами решения СЛАУ являются: метод Крамера, матричный метод и метод Гаусса. Первые два метода применимы только для систем с квадратной невырожденной матрицей. Методом Гаусса можно решать любую СЛАУ.
Формулы Крамера
Если определитель 
СЛАУ уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое может быть найдено по формулам:
, 
,…, 
,
где 
– определитель системы,
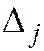– вспомогательные определители, которые получаются из определителя заменой столбца коэффициентов при 
столбцом свободных членов:
, (
).
Эти формулы называются формулами Крамера.
Задача 1.2.1
Решите СЛАУ 
,используя формулыКрамера.
Решение
Определитель системы:
Вспомогательные определители:
,
,
.
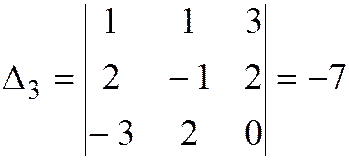По формулам Крамера: 
, 
, 
.
Матричный метод
СЛАУ уравнений с неизвестными можно записать в виде матричного уравнения
,
где
– матрица системы,
– столбец неизвестных,
– столбец свободных членов.
Если матрица 
невырожденная, то существует обратная матрица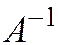 
и, умножая обе части матричного уравнения на 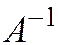слева, получим:
|
|
|
, 
, 
.
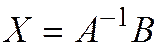Задача 1.2.2
Решите матричным методом СЛАУ 
.
Решение
Матрица системы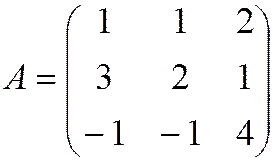 
, столбец неизвестных 
и столбец свободных членов 
.
Определитель матрицы равен:
Союзная матрица:
.
Союзная транспонированная матрица:
.
Обратная матрица:
.
Теперь можно получить решение системы в матричном виде:
замечание
Иногда требуется решить матричное уравнение вида: 
. Если – квадратная невырожденная матрица, то решение этого уравнения имеет вид: 
.
Задача 1.2.3
Решите матричное уравнение , где 
, 
.
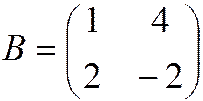Решение
Решением этого матричного уравнения является матрица 
, которая определяется по формуле:
.
Поскольку 
,
,
то
.
Проверка
.
Метод Гаусса
Рассмотрим СЛАУ систему уравнений с неизвестными
.
Матрица системы, к которой присоединен столбец свободных членов, отделенный от других столбцов вертикальной чертой, называется расширенной матрицей системы.
Определение
Элементарными преобразованиями в расширенной матрице системы называются преобразования, не меняющие множества ее решений.
К элементарным преобразованиям относятся следующие преобразования:
1) перемена местами строк матрицы;
2) умножение (деление) строки на число, отличное от нуля;
4) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно, и то же число;
5) вычеркивание одной из двух пропорциональных (равных) строк;
6) вычеркивание нулевой строки;
7) перемена местами столбцов, кроме последнего за чертой с запоминанием, какому неизвестному соответствует каждый столбец.
Принято знак элементарных преобразований обозначать: ~.
Целью метода Гаусса является приведение элементарными преобразованиями расширенной матрицы системы к такому виду, чтобы в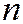 
первых ее столбцах сформировалась единичная матрица.
|
|
|
Задача 1.2.4
Решите систему методом Гаусса 
.
Решение
Расширенная матрица системы:
Шаг – формирование первого столбца
Шаг – формирование второго столбца.
шаг – формирование третьего столбца.
Решение системы, которая соответствует полученной расширенной матрице, очевидно 
.
Однородные системы
Однородная СЛАУ уравнений с неизвестными записывается в виде:
.
Однородная СЛАУ всегда совместна, она всегда имеет нулевое (тривиальное) решение: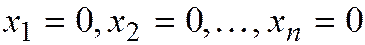 
.
Если матрица A однородной системы – квадратная, то однородная система имеет ненулевые решения тогда и только тогда, когда 
Если матрица A однородной системы не является квадратной, то выяснить, есть ли у нее ненулевые решения, можно методом Гаусса.
Определение
Пусть однородная СЛАУ имеет k ненулевых решений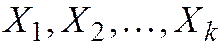 
. Эти решения образуют фундаментальную систему, если любое решение системы 
, можно представить в виде:
Задача 1.3.1
Имеет ли однородная СЛАУ 
ненулевые решения? Если да, то найти их, выписав фундаментальную систему.
Решение
Выпишем расширенную матрицу системы и преобразуем ее по методу Гаусса.
Выпишем систему, которая соответствует полученной расширенной матрице.
, 
.
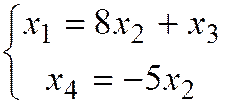Неизвестные 
и 
называются базисными. Неизвестные 
и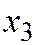 
– свободными, их можно задавать произвольно.
Чтобы получить фундаментальную систему решений, обозначим свободные неизвестные:
и 
,
где 
– любые вещественные числа. Выпишем решение системы 
в матричном виде:
.
или
,
где решения 
и 
образуют фундаментальную систему решений.
|
|
|
