Главная | Обратная связь | Поможем написать вашу работу!

Общее исследование функции для построения её графика

Использование производной при исследовании функций сообщает многое о поведении функции, но не все. Есть моменты в исследовании, не связанные с дифференцированием, но, тем не менее очень важные для построения графика функции. Рассмотрим эти моменты в рамках общей схемы исследования функций с целью построения ее графика.

1) Нахождение области определения функции, т.е. указание тех значений переменной, при которых функция существует.

2) Определение четности (нечетности) функции.

3) Определение точек пересечения графика с осями координат.

Точками пересечения с осью абсцисс (OX) являются корни функции, т.е. те значения переменной х, при которых .

Точками пересечения с осью ординат (OY) являются точки с координатами

4) Определение промежутков знакопостоянства функции.

Промежутки, на которых функция сохраняет свой знак, можно найти методом интервалов, нанеся на числовую ось корни функции и точки разрыва (это те точки, в которых может происходить смена знака).

5) Нахождение асимптот графика функции.

Асимптотой графика функции называется прямая, к которой стремится график при бесконечном удалении от начала координат.

Асимптоты делятся на три вида: горизонтальные, вертикальные и наклонные.

Горизонтальная асимптота определяется уравнением вида , где b – имеет конечное значение и определяется из условия (если пределы при совпадают, то у функции одна горизонтальная асимптота, если пределы различны – то две).

Прямая является вертикальной асимптотой графика функции , если хотя бы один из пределов или равен +¥ или –¥. В качестве а выбирают точки разрыва функции или границы области определения.

Наклонная асимптота определяется уравнением , где k и b определяются из условий:

Примечание: так же, как и в случае с горизонтальной асимптотой, пределы при могут быть одинаковыми, а могут быть различными. Наклонная асимптота имеется, если и k, и b имеют конечные значения.

6) Определение промежутков возрастания и убывания, исследование на экстремум. Определение промежутков выпуклости и вогнутости графика функции.

Эти вопросы рассмотрены в начале раздела.

При построении графика функции вначале на координатной плоскости отмечают пунктиром или тонкой чертой асимптоты графика функции, если они имеются. Затем отмечают точки пересечения с осями координат, если они есть, и экстремумы функции. После этого рисуют график функции, сообразуясь со знаками функции, возрастанием или убыванием, характером выпуклости или вогнутости, поведением вблизи асимптот.

Пример. Исследовать функцию и построить ее график.

1) Областью определения являются все значения x, кроме .

2) Т.к. , то функция нечетная.

3) График функции проходит через начало координат, т.к. при .

4) Для определения промежутков знакопостоянства функции нанесем на числовую ось точки и , в которых она может менять знак, и определим знак функции в полученных интервалах.

5) Исследуем наличие асимптот у графика функции.

следовательно, горизонтальной асимптоты нет.

Исследуем точки разрыва функции.

Прямые будут вертикальными асимптотами.

Для определения наклонной асимптоты составим пределы:

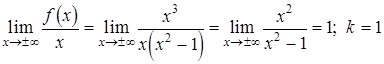Уравнение наклонной асимптоты .

6) Находим первую производную функции:

Критические точки производной . Наносим их на числовую ось и определяем знаки производной:

На промежутке функция возрастает, на 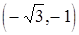, , 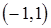– убывает, на промежутке – снова возрастает. При у функции имеется максимум, равный ; при у функции имеется минимум, равный .