 |
Частные производные функции нескольких переменных
|
|
|
|
Элементы теории функции нескольких переменных
Примеры и определение функции нескольких переменных
Существует большое количество величин, которые зависят от нескольких других. Например, падение напряжения на резисторе U зависит от силы тока I и сопротивления R:  .
.

|
Объем комнаты V зависит от длины l, ширины d и высоты h:  .
.
Расстояние r от начала координат до точки A зависит от трех ее координат
 .
.
Температура  в каждой точке нагретого тела зависит от четырех переменных - координат точки
в каждой точке нагретого тела зависит от четырех переменных - координат точки  и времени
и времени 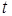 :
:
 .
.
Эти и еще множество других зависимостей можно объединить понятием функции нескольких переменных.
Если каждому набору значений переменных  соответствует вполне определенное значение величины y, то говорят, что y является функцией n переменных, и записывают
соответствует вполне определенное значение величины y, то говорят, что y является функцией n переменных, и записывают
 .
.
Для функций нескольких переменных могут использоваться и другие обозначения, например:
 .
.

|
Областью определения функции нескольких переменных называется совокупность значений переменных, при которых функция имеет смысл.
Пример. Найти и изобразить область определения функции
 .
.
Так как на множестве действительных чисел логарифм можно найти только от положительных чисел, то должно выполняться условие:
 или
или  .
.
Подстановкой значений переменных можно убедиться, что это часть плоскости, лежащая выше прямой  .
.
Способы задания, графическое изображение
Рассмотрим способы задания функции нескольких переменных.
1. Аналитический способ.
а) Функция задана в явном виде формулой  , позволяющей по значениям переменных вычислить значение функции, например,
, позволяющей по значениям переменных вычислить значение функции, например,  .
.
б) Функция задана в неявном виде соотношением 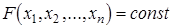 , связывающим значение функции и переменные, например,
, связывающим значение функции и переменные, например,  ;
;  .
.
|
|
|
2) Табличный способ задания функции нескольких переменных.
Практически этот способ удобен только для функции двух переменных:

| y 1 | y 2 | ... | ym | |
| x 1 | z 11 | z 12 | ... | z 1 m | |
| x 2 | z 21 | z 22 | ... | z 2 m | |
| ... | ... | ... | ... | ... | |
| xn | zn 1 | zn 2 | ... | znm |

|
3) Графическое изображение функции нескольких переменных.
Функцию одной переменной можно изобразить графически линией. Функцию двух переменных можно изобразить поверхностью. Например, на рисунке представлено изображение поверхности, задаваемой уравнением  . Поверхность, заданная уравнением такого вида, называется параболоидом.
. Поверхность, заданная уравнением такого вида, называется параболоидом.

|
Уравнение сферы с центром в начале координат  представляет собой неявную функцию двух переменных, которая может быть представлена двумя явными функциями:
представляет собой неявную функцию двух переменных, которая может быть представлена двумя явными функциями:
 и
и 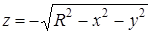 .
.
Линией уровня функции двух переменных называется линия, на которой функция сохраняет постоянное значение. Например, линиями уровня функции  будут окружности различного радиуса
будут окружности различного радиуса
 .
.
Поверхностью уровня функции трех переменных называется поверхность, на которой она сохраняет постоянное значение. Например для функции трех переменных  поверхностями уровня будут плоскости, уравнения которых имеют вид
поверхностями уровня будут плоскости, уравнения которых имеют вид 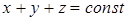 .
.
Функция большего числа переменных также может принимать постоянные значения, но объект, соответствующий совокупности значений переменных, для которых функция принимает постоянное значение, представить графически нельзя. Тем не менее, по аналогии с функциями трех переменных, его называют поверхностью или гиперповерхностью уровня.
Частные производные функции нескольких переменных
Частным приращением  функции нескольких переменных
функции нескольких переменных  по переменной
по переменной 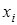 называется разность:
называется разность:
 ,
,
где  – приращение переменной
– приращение переменной 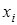 .
.
Частной производной  функции
функции  по переменной
по переменной 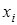 называется предел отношения частного приращения
называется предел отношения частного приращения  к приращению
к приращению  , когда последнее стремится к 0 произвольным образом:
, когда последнее стремится к 0 произвольным образом:
 .
.
Учитывая соответствующие обозначения, для функции двух переменных получим:
|
|
|
 ;
;
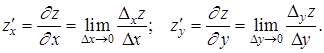
Частные производные функции нескольких переменных можно найти по правилам дифференцирования и таблице производных для функции одной переменной, т.к. при дифференцировании по одной переменной 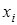 все остальные переменные имеют постоянное значение. Рассмотрим несколько примеров для функции двух переменных.
все остальные переменные имеют постоянное значение. Рассмотрим несколько примеров для функции двух переменных.
1)  ;
;
 ;
;

2)  .
.
Дифференцирование сложной функции нескольких переменных рассмотрим на примере функции двух переменных.
Пусть  , а
, а 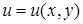 . Тогда
. Тогда
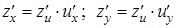 .
.
Пример. 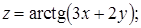

Пусть  , а
, а  , тогда
, тогда  - сложная функция от
- сложная функция от 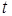 . Производную
. Производную  можно найти аналогично производной сложной функции одной переменной:
можно найти аналогично производной сложной функции одной переменной:

Пример. Найти  , если
, если  .
.

|
|
|


