 |
Примеры исследования на экстремум
|
|
|
|
Исследование функции нескольких переменных на экстремум
Определение экстремума
Набору значений двух переменных 
и 
соответствует точка на плоскости, набору значений трех переменных 
– точка в пространстве. По аналогии набор значений нескольких переменных 
будем называть точкой М, набор значений 
будем называть точкой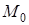 
.
Нарисуем на плоскости круг с центром в точке 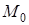и радиусом 
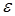. Для всех точек этого круга расстояние до 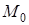не превосходит :
.
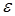Будем называть такой круг 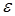-окрестностью точки 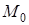. Аналогично, для произвольного числа переменных 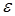-окрестностью точки 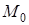называется множество точек 
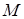, для которых выполняется условие:
.
Используя введенные понятия, дадим определение экстремума функции нескольких переменных. Функция 
имеет в точке 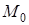максимум(минимум, если существует такая 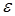-окрестность точки 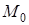, для всех точек которой выполняется условие: 
.
Если составить приращение 
, то в точке минимума приращение всегда положительно (
), в точке максимума – отрицательно (
).
Необходимые и достаточные условия экстремума
Рассмотрим функцию двух переменных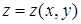 
. Пусть в точке 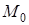у нее имеется экстремум. Зафиксируем значение одной из переменных, например, возьмем 
, тогда функция 
является функцией одной переменной, и для нее в точке экстремума должно выполняться условие: производная равна 0 или не существует. Во втором случае функция имеет так называемый «острый» экстремум. Такие функции достаточно редки, поэтому в дальнейшем будем рассматривать только функции с «гладкими» экстремумами, когда производная равна 0: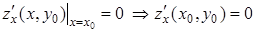 
. Аналогично можно показать, что и 
. Продолжая рассуждения для функции произвольного числа переменных, можно показать, что необходимым условием существования экстремума функции нескольких переменных является равенство 0 всех частных производных функции:
|
|
|
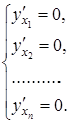
Точки, которые являются решением этой системы, называются стационарными. Чтобы узнать, будут ли они точками экстремума, и, если да, то какого, нужно проверить выполнение достаточных условий экстремума.
Для функции нескольких переменных, также, как и для функции одной переменной можно написать формулу Тейлора в следующем виде:
При малых дифференциалах независимых переменных (меньше 1), основной вклад в приращение дают дифференциалы малых порядков - первого, второго и т.д. Чем больше порядок, тем меньше величина слагаемого 
. Поскольку в точке экстремума все частные производные первого порядка обращаются в 0, то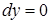 
и величина приращения определяется величиной второго дифференциала: 
.
Из этого обстоятельства следуют достаточные условия существования экстремума.
Если в стационарной точке второй дифференциал функции при любых значениях дифференциалов независимых переменных положителен, то в этой точке имеется минимум, если второй дифференциал при любых значениях дифференциалов независимых переменных отрицателен, то в этой точке имеется максимум.
Примеры исследования на экстремум
Пример 1. Исследовать на экстремум функцию 
.
Необходимые условия: 
.
Найдем вторые производные: 
. Составим дифференциал второго порядка и преобразуем его, выделив полный квадрат: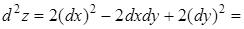 
.
Из последней формулы видно, что знак второго дифференциала в стационарной точке при любых 
и 
положителен, следовательно, в ней имеется минимум и 
.
Пример 2. Исследовать на экстремум функцию 
.
Необходимые условия: 
.
Найдем вторые производные: 
. Составим дифференциал второго порядка и преобразуем его:
.
Исследуем знак второго дифференциала в зависимости от соотношения между и :
Знак второго дифференциала зависит от значений независимых дифференциалов, значит, в исследуемой точке экстремума нет.
|
|
|
Пример 3. Исследовать на экстремум функцию
.
Необходимые условия: 
.
Вторые производные: 
.
. Видно, что знак второго дифференциала всегда положителен, значит, в исследуемой точке у функции имеется минимум и 
.
|
|
|
