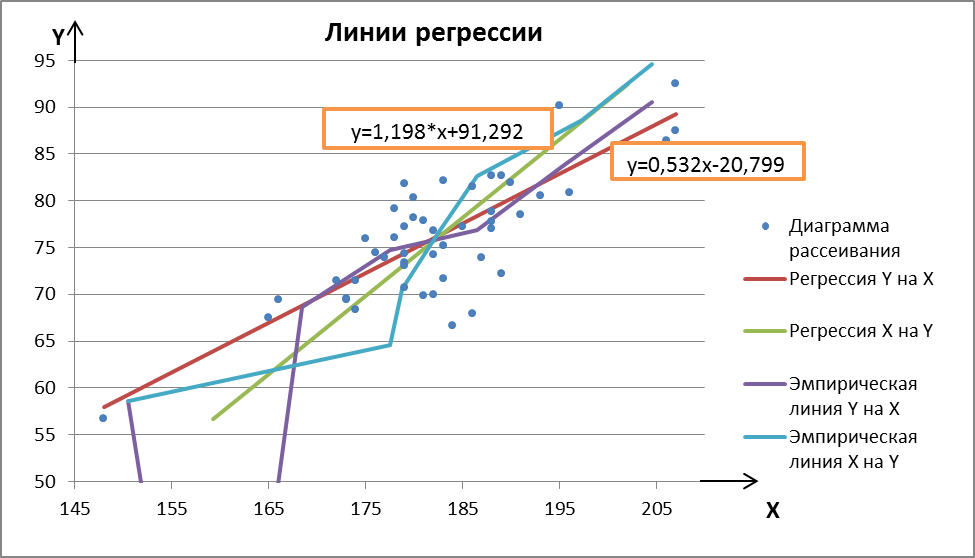
Координаты для построения эмпирической линии регрессии Y на X
xср
150,5
159,5
168,5
177,5
186,5
195,5
204,5
y(x)
58,6
0
68,6
74,7
76,9
83,8
90,6
6.4 Координаты для построения эмпирической линии регрессии X на Y
yср
58,6
64,6
70,6
76,6
82,6
88,6
94,6
x(y)
150,5
177,5
178,8
182,5
186,5
197,3
204,5
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Часть 2. Регрессионный анализ
Построение множественной модели
Множественная модель : y=-26,253 + 0,532 * x1 + 0,155 * x2
ryx1
0,7982108
- корреляция Y и X1
ryx2
0,1420646
- корреляция Y и X2
rx1x2
-0,005759
- корреляция X1 и X2
β1
0,7990555
- коэффициенты уравнения множественной регрессии в стандартном виде
β2
0,1466669
Уравнение множественной регрессии в стандартном виде:ty=β1*tx1 +β2*tx2
ty=0,799 * tx1 + 0,147 * tx2
b1
0,5323721
- коэффициенты уравнения множественной
b2
0,1550329
регрессии в естественной форме
a
-26,25324
Уравнение множественной регрессии в естественной форме:
y=a+b1*x1+b2*x2
y= - 26,253 + 0,532* x1 + 0,155 * x2
ryx1x2
0,807229666
-линейные коэффициенты
ryx2x1
0,243475679
частной
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
корреляции
rx1x2y
-0,199838054
Эyx1
1,273293821
- средние коэффициенты эластичности
Эyx2
0,069975616
Ryx1x2
0,8115731
- линейный коэффициент множественной корреляции
%
0,6586509
66%
F факт
91,65371489
- общий критерий Фишера
Fx1
89,78047885
- частные
Fx2
3,024769034
критерии Фишера
Fтабл
3,2
- табличные критерии
Fтабл
4,04
Фишера при α=0,05
Вывод:
1.
Модель допустима, ошибка аппроксимации не превосходит 8-10%;
2.
Коэффициент множественной корреляции (Ryx1x2)^2 = 0,812 характеризует зависимость y от x1 и x2 (веса от возраста и роста) как тесную, в которой 66% вариации веса определяется вариацией учтенных в модели факторов: роста и возраста. Прочие факторы не включенные в модель составляют 34%;
3.
На уровне значимости 0,05 Fтабл. = 3,2 < F факт. = 91,65 следовательно уравнение множественной модели статистически значимо и надёжно;
4.
Сравнивая F табл и F факт приходим к выводу о целесообразности включения в модель фактора x1 после фактора x2, т.к Fx1 факт=89,78> F табл=4,04;
5.
Небольшое значение Fx2 факт=3,03< F табл=4,04 свидетельствует о статической незначимости прироста ryx1^2 за счет включения в модель фактора x2 после фактора x1.
Построение парных регрессионных моделей
Линейная модель
Линейная модель: y= - 20,799 + 0,532 x
Коэф.корреляции rxy
0,798211
Средняя ошибка аппроксима
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
ции: A%
4,229623114
<8-10%
Критерий Фишера
Fтабл
4,04
Fфакт
151,55782
Вывод:
1.
Модель допустима, ошибка аппроксимации не превосходит 8-10%.
2.
Согласно критерию Фишера при уровне значимости 0,05 Fтабл=4,04 < Fфакт=151,56 уравнение линейной модели признается статически значимым и надежным, показатель тесноты связи признается значимым.
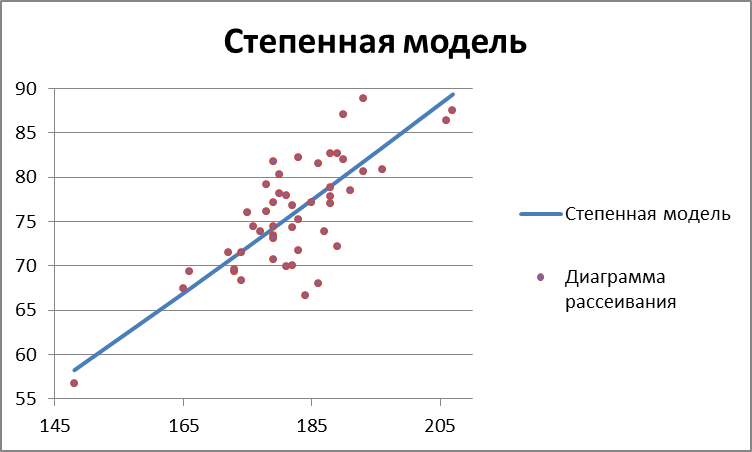
Степенная модель
Степенная модель: y= 0,0987 * x 1,277
Индекс. корреляции pxy
0,797960063
b
1,276572
a
0,098798
A
-1,00525
Средняя ошибка аппроксимации:
A%
4,232741074
<10%
Критерий Фишера
Fтабл
4,04
Fфакт
151,2747
Вывод:
1.
Модель допустима,ошибка аппроксимации не превосходит 8-10%.
2.
Согласно критерию Фишера при уровне значимости 0,05 Fтабл=4,04 < Fфакт=151,28 уравнение линейной модели признается статически значимым и надежным,показатель тесноты связи признается значимым.
3) Показатель
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
ная модель Показательная модель: y = 20,979 * 1,007 x
B
0,003062
b
1,007074288
A
1,321799
a
20,97967063
Индекс. корреляции pxy
0,796205
Критерий Фишера
Fтабл
4,04
Fфакт
149,3131
Вывод:
1.
Модель допустима, ошибка аппроксимации не превосходит 8-10%.
2.
Согласно критерию Фишера при уровне значимости 0,05 Fтабл=4,04 < Fфакт=149,31 уравнение линейной модели признается статически значимым и надежным, показатель тесноты связи признается значимым.
Гиперболическая модель
Гиперболиче
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
ская модель: y= 170,017 – 17055,1 * 1/x Индекс. корреляции pxy
0,792792
Средняя ошибка аппроксимации:
A%
4,255759302
< 10%
Критерий Фишера
Fтабл
4,04
Fфакт
145,597
Вывод:
1.
Модель допустима, ошибка аппроксимации не превосходит 8-10%.
2.
Согласно критерию Фишера при уровне значимости 0,05 Fтабл=4,04 < Fфакт=145,597 уравнение линейной модели признается статически значимым и надежным, показатель тесноты связи признается значимым.
2.2. Сравнительный анализ парных модел
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
ей
Сводная таблица:
Модель
A
Корреляция
F факт
значение
значение
значение
Линейная
4,2296
0,7982
151,55782
Степенная
4,2327
0,7980
151,27471
Показательная
4,2802
0,79620515
149,31313
Гиперболическая
4,2558
0,79279173
145,59698
Вывод:
По результатам рассматриваемых критериев самая оптимальная модель "Линейная".
2.3 Сравнение множественной модели с опт
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
имальной парной Модель
A
Корреляция
F факт
значение
значение
значение
Линейная
4,2296
0,7982
151,55782
Множественная
4,1533759
0,811573081
91,653715
Вывод:
По результатам рассматриваемых критериев самая оптимальная модель "Линейная".
Предпосылки МНК
1) Случайный характер остатка ξ = Y - Yтеор
Вывод: на основании построенного графика можно сделать вывод, что характер остатков случайный.
2)
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Нулевая средняя величина остатков независящая от нуля Вывод: Нулевая средняя величина остатковдля средних остатков равна нулю.
3) Проверка гомоскедастичности
p=1
число оцениваемых параметров
c=14
кол-во центральных наблюдений
(n-c)/2>p
Xср
173,556
- среднее значение X
Ycр
71,8056
- среднее значение Y
X*Y ср
12493,8
- среднее значение X*Y
Dx
55,2469
- дисперсия по X
Dy
23,2539
- дисперсия по Y
Линейная модель: y= - 27,228 + 0,571x
Xср
192,833
- среднее значение X
Ycр
82,2944
- среднее значение Y
X*Y ср
15893,2
- среднее значение X*Y
Dx
45,1389
- дисперсия по X
Dy
29,4283
- дисперсия по Y
Линейная модель: y= - 20,562 + 0,533x
R
3,21148
F табл.
4,45
- табличный критерий Фишера ((n-c-2*p)/2; 1) при α = 0,05
Вывод: Так как R=3,21<Fфакт=4,45 - следовательно, 3-я предпосылка выполняется, предпосылка о гомоскедатичности не нарушена.
Способ Спирмана:
∑di =38,5
Σdi 2 = 13981,25
rx,ξ
0,32863
коэффициент ранговой корреляции
t
2,41072
тест-статистика
t кр
2,0106
критическое значение
Вывод: t > tкр значит имеет место гетероскедатичность
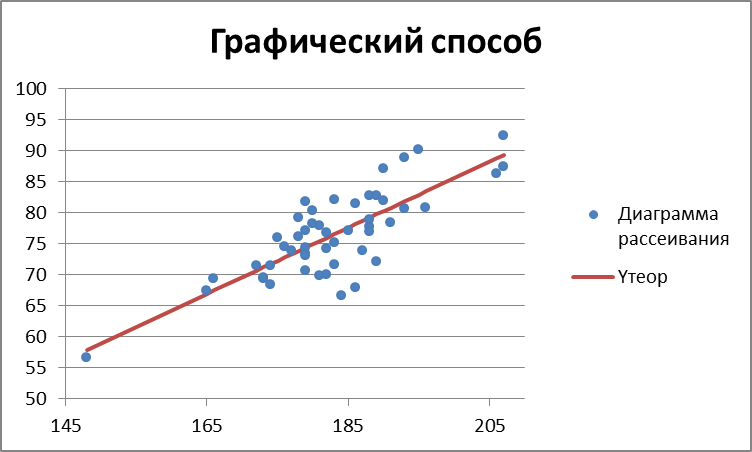
Графический способ:
Вывод: Из графика видно, что данные имеют случайный характер, имеет место гетероскедатичность.
4) Проверка отсутствия автокорреляции остатков
Применение статистики Дарбина-Уотсона
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
Лист
Дата
Подпись
№ докум.
Лист
Изм.
ПЗ 270102.14.000 МК
DW
1,770371
d1
1,32
по табл. Дарбина-Уотсона
d2
1,40
при уровне значимости α=0,01
Отрицательная автокорреляция
Зона отсутствия автокорреляции
Положительная автокорреляция
1,32
1,40
2,6
2,68
d1
d2
4-d2
4-d1
Вывод: Так как DW=1,77, то автокорреляция остатков отсутствует, следовательно, 4-я предпосылка не нарушена
Вывод:
Все предпосылки МНК выполняются. В проверке предпосылки о гомоскедатичности,существенным критерием считаем способ Гольфанда-Квандта,таким образом третья предпосылка не нарушается. Результат можно считать достоверным.
Воспользуйтесь поиском по сайту: