 |
Электропроводность металлов.
|
|
|
|
Классическая электронная теория металлов представляет твердый проводник в виде системы, состоящей из узлов кристаллической ионной решетки, внутри которой находится электронный газ из коллективизированных (свободных) электронов. В свободное состояние от каждого атома металла переходит от одного до двух электронов. К электронному газу применялись представления и законы статистики обычных газов. При изучении хаотического (теплового) и направленного под действием силы электрического поля движения электронов был выведен закон Ома. При столкновениях электронов с узлами кристаллической решетки энергия, накопленная при ускорении электронов в электрическом поле, передается металлической основе проводчика, вследствие чего он нагревается. Рассмотрение этого вопроса привело к выводу закона Джоуля - Ленца. Таким образом, электронная теория металлов дала возможность аналитически описать и объяснить найденные ранее экспериментальным путем основные законы электропроводности и потерь электрической энергии в металлах. Оказалось возможным также объяснить и связь между электропроводностью и теплопроводностью металлов. Кроме того, некоторые опыты подтвердили гипотезу об электронном газе в металлах, а именно:
1. При длительном пропускании электрического тока через цепь, состоящую из одних металлических проводников, не наблюдается проникновения атомов одного металла в другой.
2. При нагреве металлов до высоких температур скорость теплового движения свободных электронов увеличивается, и наиболее быстрые из них могут вылетать из металла, преодолевая силы поверхностного потенциального барьера.
3. В момент неожиданной остановки быстро двигавшегося проводника происходит смещение электронного газа по закону инерции в направлении движения. Смещение электронов приводит к появлению разности потенциалов на концах заторможенного проводника, и стрелка подключаемого к ним измерительного прибора отклоняется по шкале.
|
|
|
4. Исследуя поведение металлических проводников в магнитном поле, установили, что вследствие искривления траектории электронов в металлической пластинке, помещенной в поперечное магнитное поле, появляется поперечная ЭДС и изменяется электрическое сопротивление проводника.
Однако выявились и противоречия некоторых выводов теории с опытными данными. Они состояли в расхождении температурной зависимости удельного сопротивления, наблюдаемой на опыте и вытекающей из положений теории; в несоответствии теоретически полученных значений теплоемкости металлов опытным данным. Наблюдаемая теплоемкость металлов меньше теоретической и такова, как будто электронный газ не поглощает теплоту при нагреве металлического проводника. Эти противоречия удалось преодолеть, рассматривая некоторые положения с позиций квантовой механики. В отличие от классической электронной теории в квантовой механике принимается, что электронный газ в металлах при обычных температурах находится в состоянии вырождения. В этом состоянии энергия электронного газа почти не зависит от температуры, т. е. тепловое движение почти не изменяет энергию электронов. Поэтому на нагрев электронного газа теплота не затрачивается, что и обнаруживается при измерении теплоемкости металлов. В состояние, аналогичное обычным газам, электронный газ приходит при температуре порядка тысяч Кельвинов. Представляя металл как систему, в которой положительные ионы скрепляются посредством свободно движущихся электронов, легко понять природу всех основных свойств металлов: пластичности, ковкости, хорошей теплопроводности и высокой электропроводности.
|
|
|
Свойства проводников.
К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся:
1) удельная проводимость g или обратная ей величина - удельное сопротивление r,
2) температурный коэффициент удельного сопротивления ТКr или ar,
3) коэффициент теплопроводности gт,
4) контактная разность потенциалов и термоэлектродвижущая сила (термо-ЭДС),
5) работа выхода электронов из металла,
6) предел прочности при растяжении sр и относительное удлинение перед разрывом D l / l.
Удельная проводимость и удельное сопротивление проводников. Связь плотности тока J (в амперах на квадратный метр) и напряженности электрического поля (в вольтах на метр) в проводнике дается известной формулой (дифференциальная форма закона Ома):
J= g E
здесь g (в сименсах на метр) - параметр проводникового материала, называемый его удельной проводимостью: в соответствии с законом Ома у металлических проводников не зависит от напряженности электрического поля Е при изменении последней в весьма широких пределах.
Величина r = 1/g, обратная удельной проводимости и называемая удельным сопротивлением, для имеющего сопротивление R проводника длиной l с постоянным поперечным сечением S вычисляется по формуле
r = RS / l
Удельное сопротивление измеряется в ом-метрах. Для измерения r проводниковых материалов разрешается пользоваться внесистемной единицей Ом×мм2/м; очевидно, что проволока из материала длиной 1м с поперечным сечением 1 мм2 имеет сопротивление в омах, численно равно r материала в Ом×мм2/м.
Значение удельной проводимости у (или удельного сопротивления r) в основном зависит от средней длины свободного пробега электронов в данном проводнике, которая, в свою очередь, определяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению удельного сопротивления. К такому же выводу можно прийти, исходя из волновой природы электронов. Рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием около четверти длины электронной волны. Нарушения меньших размеров не вызывают заметного рассеяния волн. В металлическом проводнике, где длина волны электрона около 0,5 нм, микродефекты создают значительное рассеяние, уменьшающее подвижность электронов, и, следовательно, приводит к росту удельного сопротивления материала.
|
|
|
Температурный коэффициент удельного сопротивления металлов. Число носителей заряда (концентрация свободных электронов) в металлическом проводнике при повышении температуры практически остается неизменным. Однако вследствие усиления колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного движения свободных электронов под действием электрического поля, т. е. уменьшается средняя длина свободного пробега электрона уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов и возрастает удельное сопротивление.
Изменение удельного сопротивления металлов при плавлении. При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления r, как это видно, например для меди, из рис. 2-1; однако у некоторых металлов r при плавлении уменьшается. Удельное сопротивление увеличивается при плавлении у тех металлов, у которых при плавлении увеличивается объем, т. е. уменьшается плотность; и, наоборот, у металлов, уменьшающих свой объем при плавлении, - галлия, висмута, сурьмы r уменьшается.
Удельное сопротивление сплавов. Как уже указывалось, примеси и нарушения правильной структуры металлов увеличивают их удельное сопротивление. Значительное возрастание r наблюдается при сплавлении двух металлов в том случае, если они образуют друг с другом твердый раствор, т. е. при (утверждении совместно кристаллизуются, и атомы одного металла входят в кристаллическую решетку другого.
Теплопроводность металлов. За передачу теплоты через металл в основном ответственны те же свободные электроны, которые определяют и электропроводность металлов и число которых в единице объема металла весьма велико. Поэтому, как правило, коэффициент теплопроводности металлов намного больше, чем коэффициент теплопроводности диэлектриков. Очевидно, что при прочих равных условиях, чем больше удельная электрическая проводимость у металла, тем больше должен быть и его коэффициент теплопроводности. Легко также видеть, что при повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость g уменьшаются, отношение коэффициента теплопроводности металла к его удельной проводимости должно возрастать.
|
|
|
Термоэлектродвижущая сила. При соприкосновении двух различных металлических проводников между ними возникает контактная разность потенциалов. Причина появления этой разности потенциалов заключается в различии значений работы выхода электронов из различных металлов, а также в том, что концентрация электронов, а следовательно, и давление электронного газа у разных металлов и сплавов могут быть неодинаковыми. Из электронной теории металлов следует, что контактная разность потенциалов между металлами А и В равна:
UAB=UB - UA + (kT/e) ln (n0A/n0B)
где UA и UB - потенциалы соприкасающихся металлов;
n0A и n0B - концентрации электронов в металлах А и В;
k - постоянная Больцмана;
e - абсолютная величина заряда электрона.
Если температуры «спаев» одинаковы, то сумма разности потенциалов в замкнутой цепи равна нулю. Иначе обстоит дело, когда один из спаев имеет температуру T1, а другой - температуру Т2 ( рис. 2-2).
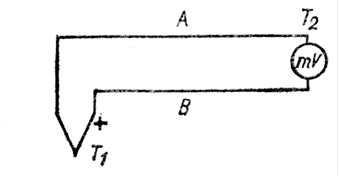
Рис. 2-2. Схема термопары
В этом случае между спаями возникает термо-ЭДС, равная:
U = (k/e) (T1 - T2) ln (n0A/n0B)
Что можно записать в виде:
U = y (T1 - T2)
где y - постоянный для данной пары проводников коэффициент термоЭДС, т. е. термо-ЭДС должна быть пропорциональна разности температур спаев.
Список используемой литературы
Нормативные документы
1. ГОСТ 8.062-85 «Государственная система обеспечения единства измерений. Государственный специальный эталон и государственная поверочная схема для средств измерений твердости по шкалам Бринелля».
2. ГЭТ 33-85 «Государственный специальный эталон единиц твердости по шкалам Бринелля».
3. ГОСТ 24621-91 (ISO 868-85) «Определение твёрдости при вдавливании с помощью дюрометра (твёрдость по Шору)».
4. ГОСТ 263-75 «Резина. Метод определения твёрдости по Шору А».
5. ГОСТ 23273-78 «Металлы и сплавы. Измерение твердости методом упругого отскока бойка (по Шору)».
6. ISO 2815 «Paints and varnishes - Buchholz indentation test».
7. DIN 53153 «Buchholz hardness».
|
|
|
8. ISO 14577 Metallic Materials. Instrumented indentation test for hardness and materials parameters. Part 1: Test method.
Литература
1. Боородицкий Н.П. Электротехнические материалы.- Л.: Энергоатомиздат, 1985
2. Проводниковые материалы / Под ред. Л.Ш. Казарновского. -М.: Энергия, 1970
3. Методические разработки к курсам “Конструкционные Материалы” и “Материаловедение” / Под ред. А.А. Клыпина. -М.: Издательство МАИ, 1993
4. Учебное пособие к лабораторным работам по металловедению. /Под ред. О.Х. Фаткуллина.- М.: Издательство МАИ
5. http://www.e-reading.org (интернет-источник)
6. http://ru.wikipedia.org (интернет-источник)
7. http://bcehaxytop.narod.ru (интернет-источник)
8. http://www.modificator.ru (интернет-источник)
|
|
|


