 |
Группа одинаковых и равноудаленных импульсов
|
|
|
|
Примеры определения спектров непериодических сигналов
Прямоугольный импульс
Этот простейший сигнал определяется выражением
,
и его график показан на рисунке ниже
Прямоугольный импульс
Спектральная плотность прямоугольного импульса
S (i ω) = 
= 
= 
= 
.
Заметим, что здесь начало отсчета времени выбрано в середине прямоугольного импульса, чтобы эта функция времени была четной. При таком выборе начала отсчета времени спектральная плотность S (i ω) является действительной функцией, которую можно обозначить как S (ω). Произведение E τи, равное площади импульса, определяет значение S (0) при ω = 0, т.е. S (0) = E τи. Очевидно, что S (0) не зависит от выбора начала отсчета времени.
Таким образом, выражение для спектральной плотности можно записать в виде
S (ω) = 
= 
,
где через 
обозначена функция вида sinc(x) = sin x / x.
На рисунке ниже представлены графики спектральной плотности прямоугольного импульса.
Спектральная плотность прямоугольного импульса
Модуль спектральной плотности прямоугольного импульса
Аргумент спектральной плотности прямоугольного импульса
При удлинении (растягивании) импульса расстояние между нулями функции S (ω) сокращается, что равносильно сужению спектра. Значение S (0) при этом возрастает. При укорочении (сжатии) импульса, наоборот, расстояние между нулями функции S (ω) увеличивается (расширение спектра), а значение S (0) уменьшается. В пределе при τи 
∞ (Е = const) точки ω1 = ±2π/τи, соответствующие двум первым нулям функции S (ω), удаляются в бесконечность и спектральная плотность, бесконечно малая по величине, становится равномерной в полосе частот от -∞ до ∞. При этом произведение длительности τ и прямоугольного импульса на его ширину спектра по первым нулям спектра 4π/τи остается равным 4π. Очевидно, что это свойство не зависит от того, как мы обозначим аргументы функций sinc(x) и ее преобразования Фурье F (y).
|
|
|
Показанные выше графики | S (ω)|/ S (0) и φ(ω) можно рассматривать соответственно как АЧХ и ФЧХ спектра прямоугольного импульса. Каждая перемена знака S (ω) учитывается приращением фазы на π.
Импульс вида sinc(x)
На рисунке ниже изображен импульс, определяемый выражением
s (t) = sinc(ωm t) = 
.
Импульс вида sinc(ωm t)
Спектральная плотность этого импульса
S (ω) = 
= 
.
Полученный интеграл не берется «в лоб» и отсутствует в известных математических справочниках. Поэтому мы воспользуемся свойством взаимозаменяемости ω и t в преобразованиях Фурье для четных функций времени.
После замены ω на t и t на ω для прямоугольного импульса видно, что функции sinc(ωm t) будет соответствовать спектр прямоугольной формы. Останется лишь найти ширину этого спектра и его уровень.
В предыдущем пункте мы нашли, что произведение длительности функции sinc(x) (по ее первым нулям) на ширину ее спектра равно 4π. Поскольку длительность функции sinc(x) равна 1/ f m, то ширина ее спектра будет равна 2ω m = 4π fm.
Уровень спектра, равномерный в полосе - ω m ≤ ω ≤ ω m, проще всего определить по его значению в точке ω = 0, для которой значение S (0) равно площади импульса:
S (0) = 
= 
.
В математических справочниках приводится значение определенного интеграла
= 
.
Таким образом,
S (0) = 
= 
= 
.
Спектр импульса вида sinc(ωm t) показан на рисунке ниже.
Спектр импульса вида sinc(ωm t)
Группа одинаковых и равноудаленных импульсов
Данный сигнал показан на рисунке ниже.
Пачка одинаковых равноудаленных импульсов
Спектральную плотность первого импульса в пачке обозначим через S 1(i ω). Тогда для второго импульса, сдвинутого относительно первого на время Т (в сторону запаздывания), спектральную плотность можно представить выражением S 2(i ω) = S 1(i ω)e- i ω T, для третьего импульса S 3(i ω) = S 1(i ω)e- i 2ω T и т.д.
|
|
|
Для группы из N импульсов в соответствии с принципом линейного суммирования спектров при сложении сигналов спектральная плотность
S (i ω) = S 1(i ω)[1 + e- i ω T + e- i 2ω T + … + e- i ( N– 1)ω T ].
При частотах, отвечающих условию ω = k 2π /T, где k – целое число, каждое из слагаемых в квадратных скобках равно единице и, следовательно,
S (ik 2π /T) = NS 1(ik 2π /T).
Таким образом, при частотах ω = k 2π /T модуль спектральной плотности пачки в N раз больше модуля спектра одиночного импульса. Это объясняется тем, что спектральные составляющие различных импульсов с указанными выше частотами складываются с фазовыми сдвигами, кратными 2π.
При частотах же ω =(1/ N)(2π /T), а также при некоторых других частотах, для которых сумма векторов e- ik ω T обращается в нуль, суммарная спектральная плотность обращается в нуль, суммарная спектральная плотность равна нулю. При промежуточных значениях частот модуль S (i ω), равный | S (iω)|, определяется как геометрическая сумма спектральных плотностей отдельных импульсов.
В качестве иллюстрации на рисунке ниже изображен модуль спектра пачки из трех (а) и четырех (б) прямоугольных импульсов при интервале между соседними импульсами
T = 3τи.
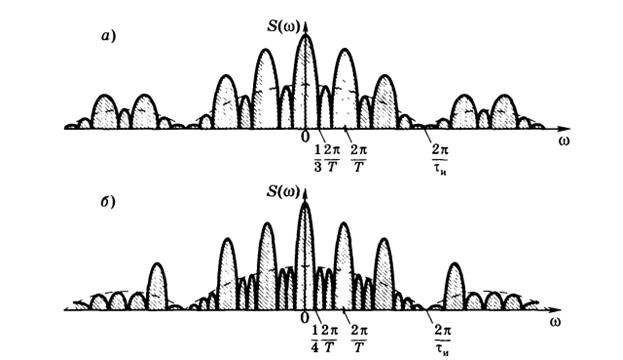
Модуль спектральной плотности пачки из трех (а) и четырех (б) импульсов
Штриховыми линиями показана спектральная плотность одиночного импульса.
С увеличением числа импульсов в пачке спектральная плотность все более расщепляется и в пределе при N ∞ принимает линейчатую структуру спектра периодической функции.
Все примеры подтверждают важное свойство преобразования Фурье: укорочение (удлинение) сигнала приводит к расширению (сжатию) его спектра.
|
|
|
