 |
Индивидуальные контрольные задания
|
|
|
|
По молекулярной физике
Вариант 1
Модуль 1
1.Исходя из биномиального распределения Р(m,n) доказать, что наиболее вероятным является состояние газа с равномерным распределением частиц по двум половинам объема: m = n/2, где n – число частиц во всем объеме V = 2n. Использовать формулу Стирлинга.
2. Электроны в полупроводниках, сталкиваясь с некоторыми атомами, так называемыми локальными центрами, могут быть ими захвачены. Сечение захвата σ зависит от кинетической энергии электрона Е 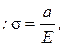 где a – константа. Определить зависимость от температуры среднего времени жизни электрона до захвата
где a – константа. Определить зависимость от температуры среднего времени жизни электрона до захвата 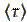 . Концентрация локальных центров захвата nц известна. Считать, что для электронов в полупроводниках справедлива статистика Максвелла.
. Концентрация локальных центров захвата nц известна. Считать, что для электронов в полупроводниках справедлива статистика Максвелла.
3. Через какое время t насос Ленгмюра откачает двухлитровый баллон с воздухом от давления  мм рт. ст. до
мм рт. ст. до 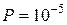 мм рт. ст., если баллон соединён с насосом трубкой длиною l = 25 см и диаметра D = 7 мм? Скорость откачки насоса K = 1000 см3/с. Температура воздуха t = 18°C.
мм рт. ст., если баллон соединён с насосом трубкой длиною l = 25 см и диаметра D = 7 мм? Скорость откачки насоса K = 1000 см3/с. Температура воздуха t = 18°C.
Модуль 2
4. Воду, находящуюся при 0 ºC и давлении Р = 100 атм, расширяют адиабатически и квазистатически до атмосферного давления. Найти изменение температуры воды в этом процессе, если коэффициент объемного расширения воды в этих условиях отрицателен и равен  ºС-1.
ºС-1.
5. Найти уравнение адиабаты для газа, уравнение состояния которого дается в виде
P = P 0(1 + α T − β V),
где постоянные a, b и Р 0 известны. Считать, что молярная теплоемкость газа сv не зависит от температуры.
6. Тепловая машина с идеальным газом в качестве рабочего вещества совершает обратимый цикл, состоящий из изохоры, адиабаты и изотермы. Рассчитать количества тепла, получаемые рабочим веществом на каждом этапе цикла. Найти к. п. д. машины как функцию максимальной и минимальной температур, достигаемых газом в этом цикле.
|
|
|
7. Один моль Н2О охлаждается от температуры t 1=25°C до t 2=0°C и замерзает. Всё тепло, полученное охлаждающей машиной, работающей с максимальной теоретически допустимой эффективностью, передаётся другому молю H2O при t 1=25°C, в результате чего его температура повышается до 100°С. Сколько молей Н2О переходит в пар при 100°С? Какую работу должен произвести рефрижератор? Теплота испарения q при 100°С равна
40,9 кДж / моль. Теплота плавления льда l при 0°С равна 6 кДж / моль.
Модуль 3
8. Записать уравнение реального газа типа Дитеричи в приведённых переменных: 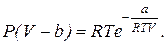
9. Один конец стержня поддерживается при температуре Т 1, а другой – при температуре Т2. Сам стержень состоит из двух частей, длины которых l 1и l 2, а коэффициенты теплопроводности c 1 и c 2. Найти температуру поверхности соприкосновения частей стержня.
10. Рассматривая удельную теплоту испарения q как работу, затрачиваемую на преодоление внутреннего давления Pi, найти зависимость между Pi, q и плотностью жидкости 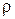 . Считать, что жидкость подчиняется уравнению Ван-дер-Ваальса.
. Считать, что жидкость подчиняется уравнению Ван-дер-Ваальса.
Вариант 2
Модуль 1
1.Допустим, что все молекулы воды в стакане как-то отмечены. После этого вода была вылита в водопроводный сток. По прошествии длительного времени вылитая вода равномерно перемешается со всей водой, имеющейся на Земле. Какое количество отмеченных молекул окажется в стакане, если его вновь наполнить водопроводной водой?
2. Определить скорость конденсации паров воды в комнате на холодном окне, если предположить, что происходит захват только тех молекул, которые налетают на поверхность стекла с составляющей энергии  . Координатная ось х перпендикулярна поверхности стекла. Процессы теплопроводности и конвекции воздуха у окна не рассматривать.
. Координатная ось х перпендикулярна поверхности стекла. Процессы теплопроводности и конвекции воздуха у окна не рассматривать.
|
|
|
3. В тонкостенный сферический баллон массы м = 1 кг нагнетается азот при температуре T = 300 К. Найти максимальное количество азота, которое можно поместить в сосуд, если допустимое напряжение в стенках баллона 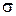 = 50 Н / мм2. Плотность стали
= 50 Н / мм2. Плотность стали  7,8 г/см3.
7,8 г/см3.
Модуль 2
4. Колесо паровоза имеет радиус r 0 = 1 м при t 0 = 0º C. Определить разницу в числах оборотов колеса летом при температуре t 1 = 25º С и зимой при температуре t 1 = −25º С на пути пробега паровоза l = 100 км. Коэффициент линейного расширения металла колеса 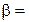 0,000012º С.
0,000012º С.
5. Основной причиной понижения температуры с высотой в атмосфере является адиабатическое расширение восходящих потоков воздуха. Используя уравнение адиабаты идеального газа, найти изменение температуры с высотой.
6. Тепловая машина Карно используется в качестве холодильной машины для поддержания температуры некоторого резервуара при температуре t 2 = –3 °С. Температура окружающего воздуха t 1 = 27 °С. Какая механическая работа требуется для выполнения одного цикла машины, если при этом от оболочки резервуара отводится Q 2 = 900 кал тепла?
7. Идеальный газ с показателем адиабаты g совершает процесс по закону Р = Р 0− a V, где Р 0 и a − положительные постоянные. При каком значении объема Vm энтропия газа окажется максимальной.
Модуль 3
8. Найти уравнение политропы для газа Ван-дер-Ваальса, считая, что его теплоемкость С v не зависит от температуры.
9. Постоянный электрический ток течёт по проводу, радиус которого R и теплопроводность χ. В единице объёма провода выделяется тепловая мощность w. Найти распределение температуры в проводе, если установившаяся температура на его поверхности равна Т 0.
10. Найти удельную теплоту испарения бензола q исп вблизи его тройной точки, если известно, что при этих условия его удельная теплота плавления q пл = 30,2 кал/г, температура тройной точки  = 279 К, равновесное давление пара в тройной точке Р = 36 мм рт. ст. и для кривой возгонки в той же точке dP/dT = 2,43 мм рт. ст. / К. Считать пар бензола идеальным газом.
= 279 К, равновесное давление пара в тройной точке Р = 36 мм рт. ст. и для кривой возгонки в той же точке dP/dT = 2,43 мм рт. ст. / К. Считать пар бензола идеальным газом.
Вариант 3
Модуль 1
1. Результат прицельной стрельбы из пистолета по мишени для начинающего спортсмена характеризуется плотностью вероятности вида:
|
|
|
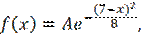
где x – число очков, выбиваемое при одном выстреле. Определите средний результат одного выстрела 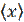 и стандартное отклонение от него σ (x).
и стандартное отклонение от него σ (x).
2. Центр тяжести линейного макроскопического тела находится на высоте h с и рассчитывается по формуле
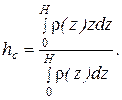
На какой высоте находится центр тяжести вертикального цилиндрического столба воздуха. Считать, что температура воздуха Т и ускорение свободного падения g не зависят координаты z, изменяющейся от 0 до ∞.
3. В ртутном барометре с правильной цилиндрической барометрической трубкой расстояние от уровня ртути в чашке до запаянного конца трубки равно L. В трубку при нормальном барометрическом давлении Н и температуре t 1 попал пузырек воздуха, благодаря чему длина ртутного столба уменьшилась и стала равной h 1. Найти выражение для поправки p 1, прибавляя которую к показанию h барометра, можно было бы пользоваться последним при любых температурах t и любых высотах h ртутного столба.
Модуль 2
4. Для определения истинного коэффициента объемного расширения жидкостей применяется следующий метод. Два сообщающихся сосуда наполняются жидкостью, расширение которой исследуется; при одинаковой температуре обоих сосудов жидкость в них находится на одной высоте. Если один из сосудов охлаждать тающим льдом, а другой нагревать в парах кипящей при нормальном атмосферном давлении воды, то при равновесии уровни жидкостей будут различны. Эта разность уровней дает возможность вычислить коэффициент объемного расширения а. Вывести выражение для а.
5. Определить, насколько отличается тепловой эффект реакции образования одного моля водяного пара при постоянном давлении от теплового эффекта той же реакции, если она происходит без совершения внешней работы.
 6. В прямоугольном цикле (см. рис.), совершаемом молем идеального газа с показателем адиабаты g, даны параметры «углов»: Р 1, Р 2, V 1, V 2. Вычислить к.п.д. цикла.
6. В прямоугольном цикле (см. рис.), совершаемом молем идеального газа с показателем адиабаты g, даны параметры «углов»: Р 1, Р 2, V 1, V 2. Вычислить к.п.д. цикла.
7. В системе, состоящей из двух сосудов объёмами V 1 и V 2, соединенных каналом, помещена газовая турбина. Массы газа, находящиеся в каждом из сосудов при температуре Т 1 и Т 2, равны между собой. Весь комплекс адиабатически изолирован. Определить максимальную работу, которая может быть совершена после открытия канала. Газ считать идеальным.
|
|
|
Модуль 3
8. Определить разность молярных теплоемкостей (Ср-Сv) для газа Ван-дер-Ваальса.
9. Стержень длиною l с теплоизолированной боковой поверхностью состоит из материала, теплопроводность которого изменяется с температурой по закону 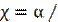 T, где α − постоянная. Торцы стержня поддерживают при температурах Т 1 и Т 2. Найти зависимость Т (
T, где α − постоянная. Торцы стержня поддерживают при температурах Т 1 и Т 2. Найти зависимость Т (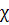 ), где
), где 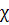 − расстояние от торца с температурой Т 1, а также плотность потока тепла.
− расстояние от торца с температурой Т 1, а также плотность потока тепла.
10. В следующей таблице приведены давления насыщенных паров азота при трех температурах:
| Р, мм рт. ст | −196 | −197 | |
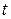 , °С , °С
| −195 |
Пользуясь ими, вычислить удельную теплоту испарения q жидкого азота при температуре t = –196 ºС. Считать, что газообразный азот вплоть до температуры конденсации подчиняется уравнению Клапейрона. Удельным объёмом жидкого азота по сравнению с газообразным пренебречь.
Вариант 4
Модуль 1
1. Вероятность того, что смещение классического гармонического осциллятора в момент времени t находится в интервале значений (x, x + 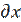 ) имеет вид:
) имеет вид:
dP = (A 2 – x 2)−1∕2 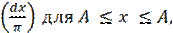
где А – амплитуда колебания осциллятора; dP = 0 для А< х< А.
Определите величину среднего отклонения осциллятора 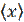 и стандартное отклонение от среднего значения σ(x).
и стандартное отклонение от среднего значения σ(x).
2. Вычислить относительную величину флуктуации энергии одной частицы двухуровневой системы на основе статистической суммы. Считать кратность вырождения верхнего уровня равным g 1, а основного уровня – g 2.
3. Фабричная труба высотою l = 50 м выносит дым при температуре t 1 = 60°С. Определить статическое давление Р, производящее тягу в трубе. Температура воздуха t 2 = –10°С. Плотность воздуха ρ0 = 1,29∙10-3 г/см3.
Модуль 2
4. Из кварца параллельно его оси вырезана круглая пластинка, радиус которой при температуре t 1 равен r. Определить площадь пластинки S при температуре t 2. Коэффициенты расширения кварца параллельно и перпендикулярно оси равны соответственно 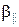 и
и 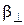 .
.
5. Имеется идеальный газ, молярная теплоёмкость CV которого известна. Найти молярную теплоёмкость этого газа как функцию его объёма V, если газ совершает процесс по закону:
а) 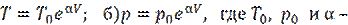 постоянные.
постоянные.

6. Определить совершаемую произвольным веществом работу цикла, состоящего из изотермы 1-2, политропы 2−3 и адиабаты 3−1. Известно, что теплоёмкость тела на политропе равна С, а температуры на изотерме и в состоянии 3 равны соответственно Т 1 и Т 2.
|
|
|
7. Один моль идеального газа совершает процесс, при котором энтропия газа изменяется с температурой Т по закону S = α T + CV ln T, где α − положительная постоянная, CV − молярная теплоёмкость данного газа при постоянном объёме. Найти, как зависит температура газа от его объёма в этом процессе, если Т = Т 0 при V = V 0.
Модуль3
8. Вычислите разность молярных теплоёмкостей Ср –С v газа, состояние которого описывается уравнением Бертло, оставляя лишь линейные члены по отношению к а и b.
9. Два теплоизолированных тела 1 и 2 с бесконечными теплопроводностями (например, два куска металла) соединены между собой однородным, также теплоизолированным стержнем длины l с площадью поперечного сечения S и теплопроводностью χ. Теплоёмкости тел 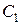 и
и 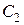 очень велики по сравнению с теплоёмкостью стержня. Найти температуры тел
очень велики по сравнению с теплоёмкостью стержня. Найти температуры тел 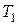 и
и 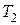 в любой момент времени t, если при t = 0 они были равны соответственно
в любой момент времени t, если при t = 0 они были равны соответственно  и
и  . Найти также разность этих температур и время
. Найти также разность этих температур и время  , по истечении которого эта разность уменьшается в два раза.
, по истечении которого эта разность уменьшается в два раза.
10. Один грамм воды, находящийся при температуре 20°С, выдавливается через изолированную пористую пробку под давлением Р 1=104 атм. в большой сосуд, где давление Р 2 =1 атм. Определить состояние, в котором находится вода после вытекания из пробки. Плотность воды предполагается неизменной как при Р 1, так и при Р 2. Теплота испарения равна 2050 Дж/г.
Вариант 5
Модуль1
1. Для расчета погрешности снятия показаний со стрелочного прибора полагают, что стрелка такого прибора может с равной вероятностью остановиться в любом месте между двумя соседними делениями шкалы. Пусть соседним делениям шкалы соответствуют значения измеряемой величины xn и xn + a, где a – цена деления. Написать распределение вероятностей dP (x), (xn £ x £ xn + a). Определить 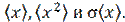
2. В сферическом реакторе с радиусом r = 1 м идет химическая реакция между газом, заполняющим реактор, и материалом стенок реактора. Продуктом реакции является порошок, непрерывно удаляемый из реактора. В реакцию могут вступить только молекулы газа, имеющие кинетическую энергию
Е ³ Еn = 1 эВ, при этом вероятность реакции при ударе молекулы о стенку
W =10-3. C какой скоростью dM/dt надо подавать газ в реактор, чтобы поддерживать в нем постоянное давление Р 0 = 10 атм? Молярная масса газа
m = 40 г/моль. Считать, что вблизи стенок реактора максвелловское распределение молекул по скоростям при температуре Т = 1160 К.
3. Цилиндрическая пипетка длиной l наполовину погружена в ртуть. Ее закрывают пальцем и вынимают. Часть ртути вытекает. Какой длины столбик ртути останется в пипетке? Атмосферное давление равно H.
Модуль 2
4. Из кварца вырезан цилиндр, ось которого параллельна оси кварца. При температуре  18 ºС радиус цилиндра
18 ºС радиус цилиндра  = 10 мм, а высота
= 10 мм, а высота 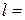 50 мм. Определить объем этого цилиндра V 2 при температуре
50 мм. Определить объем этого цилиндра V 2 при температуре 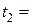 300°C. Для кварца коэффициенты линейного расширения параллельно и перпендикулярно оси равны соответственно
300°C. Для кварца коэффициенты линейного расширения параллельно и перпендикулярно оси равны соответственно 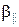 = 0,000072°C-1 и
= 0,000072°C-1 и  = 0,0000132 °C-1.
= 0,0000132 °C-1.
5. Идеальный газ с показателем адиабаты γ совершает процесс, при котором его внутренняя энергия U~V α, α − постоянная. Найти:
а) работу, которую произведёт газ, чтобы внутренняя энергия испытала приращение ∆ U;
б) молярную теплоёмкость газа в этом процессе.
6. Обратимый круговой процесс превращения теплоты в работу состоит из процесса 1−2, в котором теплоёмкость линейно нарастает с температурой от значения C1 = 20 Дж /К×моль до С2 = 50 Дж /К×моль, а также адиабаты 2−3 и изотермы 3−1. Вычислите к.п.д. этого цикла. Уравнение состояния рабочего вещества не задано. Максимальная и минимальная температуры адиабатического процесса известны.
7. Два баллона объёмом V 0 = 10−3 м каждый соединены трубкой с краном. В одном находится водород при давлении р 1 = 1,013∙105 н ∕ м 2и температуре 20°С, в другом – гелий при давлении 3 р 1и температуре 100°С. Найдите изменение энтропии системы после открытия крана и достижения равновесного состояния, если стенки баллона и трубки обеспечивают теплоизоляцию газов от окружающей среды. Газы считать идеальными.
Модуль 3
8. Получите приведённое уравнение состояния вещества, для которого справедливо второе уравнение состояния Дитеричи:

9. На дне сосуда, откачиваемого до высокого вакуума, наморожен плоскопараллельный слой льда толщиной l = 7мм, нижняя поверхность которого поддерживается при постоянной температуре t 0. Определить эту температуру, если известно, что при откачке сосуда на верхней поверхности слоя льда установилась температура t 1 = –50 ºС.
Теплопроводность льда k = 5,3 ∙10-3 кал/(с∙ см∙°С). Удельная теплота сублимации льда q = 680 кал /г. Упругость насыщенного пара надо льдом при t 1= – 50°С в отсутствие откачки равна Р = 0,03 мм рт. ст.
10. Мыльный пузырь радиуса r при пониженном давлении во внешней среде увеличил свой радиус вдвое. Считая процесс изотермическим, найти изменение энтропии мыльного пузыря. Начальное давление равно Р 0, коэффициент поверхностного натяжения мыльной пленки s, удельная теплота образования единицы поверхности пленки q. Считать, что 2s/ r << P 0.
Вариант 6
Модуль 1
1. Космический корабль, бороздящий просторы вселенной, врямя от времени испытывает столкновения с метеоритами. Предположим, что метеориты равномерно распределенены в пространстве и во времени, тогда вероятность столкновения их в момент времени определяется показательной функцией:
dP (t) =e − t dt.
Рассчитайте среднее время до ближайшего столкновения корабля с метеоритом 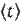 и стандартное отклонение σ (t).
и стандартное отклонение σ (t).
2. При каком значении температуры число молекул, находящихся в пространстве скоростей в фиксированном интервале (u, u + du), максимально? Продемонстрировать полученный результат с помощью графиков плотности вероятности f (u) при разных температурах.
3. Найти число ходов n поршня, чтобы поршневым воздушным насосом откачать сосуд ёмкостью V от давления Р 1 до давления Р 2, если ёмкость хода поршня равнаv. Вредным пространством пренебречь.
Модуль 2
4. Стальной бандаж нагоняется на вагонное колесо при температуре
t 1 = 300°C. Определить силу натяжения Т в бандаже при температуре
t 0 = 20ºС, если сечение бандажа S = 20 cм2. Модуль Юнга Е = 2,1∙ 107 Н/см2 и коэффициент линейного расширения 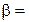 12∙ 10-6º С-1.
12∙ 10-6º С-1.
5. Для получения газов при сверхвысоких температурах и давлениях иногда применяется установка, состоящая из закрытого с одного конца цилиндра-ствола и поршня-пули, влетающей в цилиндр с открытой стороны. При хорошей обработке ствола и пули удается добиться малой утечки газа через зазор. Благодаря очень высоким температурам сильно сжатые газы в этих условиях еще можно считать идеальными. Оценить верхний предел температуры Т, давления Р и плотности р аргона, подвергнутого сжатию в такой установке, если пуля массы m = 100 г влетает в ствол, имеющий объем V = 200 cм3, с начальной скоростью v = 250 м/с. Начальные температура и давление соответственно равны T = 300 К и Р 0 = 1 атм.
6. Тепловая машина с идеальным газом в качестве рабочего вещества совершает обратимый цикл, состоящий из изобары, адиабаты и изотермы. Найти к. п. д. машины как функцию максимальной и минимальной температур рабочего вещества, используемого в этом цикле. Найти также количества тепла, получаемые рабочим веществом на каждом этапе цикла.
7. Определите энтропию тела, для которого справедливы следующие соотношения:
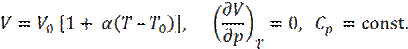
(V 0, α, T 0 – постоянные).
Модуль 3
8. Если температура газа ниже так называемой температуры Бойля, то при изотермическом сжатии его произведение PV сначала убывает, проходит через минимум, а затем начинает возрастать. Если же температура газа выше температуры Бойля, то при изотермическом сжатии произведение PV монотонно возрастает. Убедиться в этом и выразить температуру Бойля через критическую температуру для газа, подчиняющегося уравнению Ван-дер-Ваальса.
9. В тонкостенный замкнутый металлический сосуд с общей поверхностью S налита жидкость при температуре 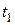 . Через сколько времени τ жидкость охладится до температуры
. Через сколько времени τ жидкость охладится до температуры 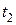 , если масса ее
, если масса ее 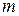 , удельная теплоёмкость с, температура воздуха вне сосуда
, удельная теплоёмкость с, температура воздуха вне сосуда 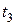 , а коэффициент теплообмена на границе металл – воздух равен
, а коэффициент теплообмена на границе металл – воздух равен  ?
?
10. Найти коэффициент объемного расширения  , изотермическую сжимаемость γТ и теплоёмкость
, изотермическую сжимаемость γТ и теплоёмкость 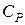 неоднородной равновесной системы, состоящей из жидкости и её насыщенного пара.
неоднородной равновесной системы, состоящей из жидкости и её насыщенного пара.
Вариант 7
Модуль 1
1. Исходя из распределения Пуассона  , найти средний квадрат флуктуации числа частиц в некотором малом объеме газа.
, найти средний квадрат флуктуации числа частиц в некотором малом объеме газа.
2. Считая, что тепловые скорости эмитируемых электронов в цилиндрическом диоде распределены по закону Максвелла с температурой Т, найти среднее значение < u ^>, сравнить его с величиной < u >.
3. Два сосуда А и В с воздухом соединены между собой капилляром с краном. Сосуд А погружен а водяную ванну с температурой t 1 = 100°С, а сосуд В – в охлаждающую смесь с температурой t 2 = –20 °С. Вначале сосуды были разобщены друг от друга краном, и давления воздуха в сосудах А и В были равны соответственно P 1 = 400 мм рт. ст. и Р 2 = 150 мм рт. ст, Найти давление, установившееся после открытия крана, если объём А равен V 1 = 250 см3, а объём В равен V 2 = 400 см3.
Модуль 2
4. Для измерения температуры термостата применили железную проволочку, имеющую при температуре 18ºС сопротивление 15 Ом. В термостате ее сопротивление оказалось равным 18,25 Ом. Определить температуру термостата t, если температурный коэффициент сопротивления железа k = 0,006ºС-1.
5. Моль идеального газа с постоянной теплоемкостью C V заключен в цилиндр с адиабатическими стенками и поршнем, который может перемешаться в цилиндре без трения. Поршень находится под постоянным внешним давлением P 1. В некоторый момент времени внешнее давление скачкообразно уменьшают или увеличивают до P 2. (Этого можно достигнуть, снимая часть груза с поршня или добавляя новый груз.) В результате газ адиабатически изменяет свой объем. Вычислить температуру и объем газа после того, как установится термодинамическое равновесие.
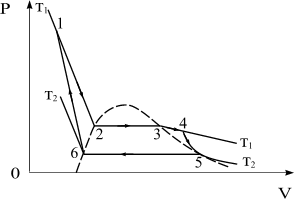 6. Какую работу совершает за один цикл 1234561 машина Карно, рабочим телом которой является один моль воды, испытывающий во время работы машины фазовые превращения в пар и обратно (см.рис.). Изотермам 1234 и 56 соответствуют температуры
6. Какую работу совершает за один цикл 1234561 машина Карно, рабочим телом которой является один моль воды, испытывающий во время работы машины фазовые превращения в пар и обратно (см.рис.). Изотермам 1234 и 56 соответствуют температуры 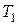 = 500 К и
= 500 К и 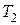 = 373 К. Нижняя изотерма 56
= 373 К. Нижняя изотерма 56
(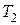 = 373 К) целиком лежит в двухфазной области вещества, так что в 6 имеется только жидкость, а в 5 – только пар. Кривые 16 и 45 – адиабаты. Удельная теплота парообразования воды q = 2,25 кДж/г (при
= 373 К) целиком лежит в двухфазной области вещества, так что в 6 имеется только жидкость, а в 5 – только пар. Кривые 16 и 45 – адиабаты. Удельная теплота парообразования воды q = 2,25 кДж/г (при  = 373 К).
= 373 К).
7. Найдите максимальную работу, которую можно получить от двух одинаковых твёрдых тел (с температурой Т 1 и Т 2) при выравнивании их температур.
Модуль 3
8. Запишите приведённое уравнение состояния для веществ, подчиняющихся уравнению состояния Бертло
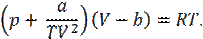
9. В тонкостенный замкнутый металлический сосуд налита жидкость, имеющая температуру 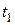 . Температура воздуха вне сосуда
. Температура воздуха вне сосуда 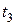 . Найти температуру
. Найти температуру 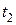 внешней стенки, если известно, что теплопроводность металла
внешней стенки, если известно, что теплопроводность металла 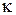 , коэффициент теплообмена на границе металл – воздух
, коэффициент теплообмена на границе металл – воздух  , а на границе металл – жидкость ∞. Толщина стенки равна L.
, а на границе металл – жидкость ∞. Толщина стенки равна L.
Примечание: Сосуд считается тонкостенным, когда толщина стенок мала по сравнению с его линейными размерами.
10. Найти изменение температуры 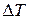 плавления льда при повышении давления на
плавления льда при повышении давления на  = 1 атм. Удельный объем воды при 0º С v ж = 1 см3/г, удельный объём льда v л = 1,091 см3/г, удельная теплота плавления льда q = 80 кал/г. По найденному значению
= 1 атм. Удельный объем воды при 0º С v ж = 1 см3/г, удельный объём льда v л = 1,091 см3/г, удельная теплота плавления льда q = 80 кал/г. По найденному значению 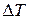 рассчитать приближенно температуру тройной точки воды.
рассчитать приближенно температуру тройной точки воды.
Вариант 8
Модуль 1
1. В результате извержения одного из вулканов на Камчатке над Землей образовалось облако, состоящее из частиц различной массы. Распределение частиц в облаке по массам в интервале 1 г £ m £ 103 г описывается функцией f(m)= 104× m -2. Предполагается, что частицы падают на Землю с постоянной для каждой частицы скоростью. Вычислить кинетическую энергию общего количества упавших частиц. Считать, что частицы имеют сферическую форму и плотность r= 4 г/см3. Вязкость воздуха h = 1,8×10-4 дн×с/см2.
2. Вычислить относительную величину флуктуации энергии идеального одномерного квантового осциллятора на основе статсуммы.
3. Определить постоянную адиабаты для газовой смеси, содержащей v1 молей водорода и v2 молей гелия. Рассмотреть частный случай, когда смесь содержит одинаковые (по массе) количества этих газов.
Модуль 2
4. Какую силу F надо приложить к стальному стержню сечением в 1 см2, чтобы растянуть его настолько же, насколько он удлиняется при нагревании на  1° С. Коэффициент линейного расширения
1° С. Коэффициент линейного расширения 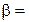 12∙10-6 ºС-1. Модуль Юнга
12∙10-6 ºС-1. Модуль Юнга 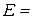 2,1∙ 107 Н/см2.
2,1∙ 107 Н/см2.
5. Моль идеального газа нагревают в цилиндре под поршнем, удерживаемым в положении равновесия пружиной, подчиняющейся закону Гука. Стенки цилиндра и поршень адиабатические, а дно проводит тепло. Начальный объем газа 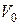 , при котором пружина не деформирована, подобран так, что
, при котором пружина не деформирована, подобран так, что  , где
, где  – наружное атмосферное давление, S – площадь поршня, k – коэффициент упругости пружины. Найти теплоёмкость газа этого процесса.
– наружное атмосферное давление, S – площадь поршня, k – коэффициент упругости пружины. Найти теплоёмкость газа этого процесса.
6. Найдите зависимость поверхностного натяжения σ от абсолютной температуры, исходя из рассмотрения бесконечно малого цикла Карно между температурами Т и Т−dT, совершаемого плёнкой жидкости.
7. Определите максимальную работу, которую можно получить с помощью твёрдого тела при охлаждении его от температуры Т до температуры Т 0 (при неизменном объёме).
Модуль 3
8. Запишите приведённое уравнение состояния для веществ, подчиняющихся уравнению состояния Клаузиуса
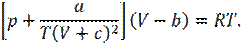
9. Сколько каменного угля нужно сжигать в течение времени τ, равного одним суткам, на водяное отопление дома, площадь поверхности стен и крыши которого равна S = 10 000 м2, чтобы поддерживать в квартирах температуру t 1 = l8 °C, если температура снаружи здания t 2 = –22° C? Толщина стен 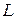 = 60 см, теплопроводность материала стен χ = 0,002 кал/(с∙ см∙ °С), а утечка тепла с единицы поверхности крыши такая же, как с единицы поверхности стены. Удельная теплота сгорания угля
= 60 см, теплопроводность материала стен χ = 0,002 кал/(с∙ см∙ °С), а утечка тепла с единицы поверхности крыши такая же, как с единицы поверхности стены. Удельная теплота сгорания угля 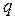 = 7500 кал/г, коэффициент теплообмена на границе воздух – стена
= 7500 кал/г, коэффициент теплообмена на границе воздух – стена  = 0,00025 кал/с∙ см2∙°С.
= 0,00025 кал/с∙ см2∙°С.
10. Идеальная холодильная машина, работающая по обратному циклу Карно, передаёт тепло от холодильника с водой при температуре 0° С кипятильнику при температуре 100°С. Какое количество воды надо заморозить в холодильнике, чтобы превратить в пар 3 кг воды в кипятильнике? Удельная теплота парообразования и удельная теплота плавления соответственно равны 2,3∙106 дж∕кг и 3,4∙105 дж∕кг.
Вариант 9
Модуль 1
1. Батарея с электродвижущей силой V замкнута на сопротивление R. Мощность, рассеиваемая на этом сопротивлении, равна Р = V 2∕ R. Сама батарея состоит из N индивидуальных элементов, соединённых последовательно, так что V равно сумме электродвижущих сил всех этих элементов. Так как батарея работала долго, то не все элементы находятся в хорошем состоянии. Пусть р – вероятность того, что э.д.с. отдельной ячейки имеет своё нормальное значение v, а q = 1 – p есть вероятность того, что э.д.с. ячейки по каким-то причинам, например из-за внутреннего закорачивания, равна нулю. Отдельные ячейки статистически независимы. Вычислите при этих условиях среднюю мощность Р, рассеянную в сопротивлении, и выразите результат через N, v, p и R.
2. Ежегодно на окраинах Гренландии образуется от 10 до 15 тысяч айсбергов. Ледяные горы дрейфуют в южные широты, создавая смертельную опасность судам. Самый известный трагический исход – гибель «Титаника». Рассчитать среднюю кинетическую энергию айсберга. Предполагается, что линейный размер айсберга L – случайная величина: 1 км £ L £ 150 км. А его толщина Н – величина постоянная и равна 0,3 км. Распределение айсбергов по размерам описывается функцией f (L) = L- 2. Скорость дрейфа льдины 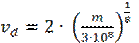 км/час, m измеряется в тоннах.
км/час, m измеряется в тоннах.
3. При взрыве атомной (урановой) бомбы в её центре достигаются температуры порядка Т ≈10 кэВ. Принимая ориентировочно плотность урана в центре бомбы равной ρ = 20 г∕см3, найти давление внутри бомбы при этой температуре. Сравнить это давление с давлением в центре Земли, вычисленным в предположении, что плотность Земли постоянна и равна ρз = 5,5 г∕см3. Давление светового давления не учитывать.
Модуль 2
4. Ртуть, находящуюся при 0 °С и давлении Р = 100 атм, расширяют адиабатически и квазистатически до атмосферного давления. Найти изменение температуры ртути в этом процессе, если коэффициент объёмного расширения ртути в этих условиях положителен и равен 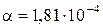 ºС-1, удельная теплоемкость ртути ср = 0,033 кал/(г°С), плотность р = 13,6 г/см3.
ºС-1, удельная теплоемкость ртути ср = 0,033 кал/(г°С), плотность р = 13,6 г/см3.
5. Вычислите коэффициенты объёмного расширения 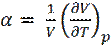 и изотермической сжимаемости
и изотермической сжимаемости  для идеального газа при нормальных условиях.
для идеального газа при нормальных условиях.
6. Окись углерода массой 5 кг расширяется при постоянном давлении, совершая работу в 105 дж, затем охлаждается до прежней температуры, после чего сжимается изотермически до первоначального объёма. Изобразите цикл на диаграмме рV и определите:
а) температуру в конце изобарического расширения;
б) количество теплоты, полученной системой при изобарическом процессе;
в) к.п.д. цикла.
Начальная температура Т 1=373°К, теплоёмкость Ср = 0,23 ккал∕(кг∙град) и C V = 0,15 ккал∕(кг∙град).
7. Найдите максимальную работу, которую можно получить при охлаждении идеального газа от температуры Т до Т 0, сопровождающемся расширением, при котором давление меняется от р до р 0.
Модуль 3
8. Покажите, что для веществ, подчиняющихся одному и тому же закону соответственных состояний, коэффициенты объёмного расширения обратно пропорциональны критическим температурам, то есть
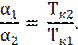
9. Определить количество тепла Q, теряемое 1 м2 стены в течение времени 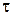 , равного одним суткам, при температуре воздуха в помещении
, равного одним суткам, при температуре воздуха в помещении
t 1 = 20°C и температуре наружного воздуха t 4 = –10°C. Толщина стены l= 20см. Теплопроводность материала стены 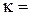 0,003 кал/(с⋅ см2⋅ °С). Коэффициент теплообмена на границе стена – воздух
0,003 кал/(с⋅ см2⋅ °С). Коэффициент теплообмена на границе стена – воздух  = – 0,0002 кал/(с⋅ см2⋅ ºС). Определить также температуры внутренней t 2 и внешней t 3 поверхностей стены.
= – 0,0002 кал/(с⋅ см2⋅ ºС). Определить также температуры внутренней t 2 и внешней t 3 поверхностей стены.
10. Определите, как зависит удельный объём пара от температуры для проце
|
|
|


