 |
Задания для самостоятельной работы
|
|
|
|
Сравните два флористических района по числу видов, используя следующие показатели. В одном флористическом районе насчитывется 225 видов (n1), в другом – 302 (n2). Общими из них оказались 57 видов.
Абсолютные и относительные данные
Абсолютные данные по заболеваемости населения редко пригодны для анализа без их предварительной обработки. Приведем пример. При проверке зрения у учащихся в школе №1 из 490 обследованных выявлено 25 случаев близорукости, а в школе №2 из 1240 – 43. Нужно сравнить эти показатели и сделать вывод, отличаются ли данные школы по распространенности близорукости. Казалось бы, можно сделать вывод, что в школе №2 близорукость распространена в большей степени. Однако при сравнении данных не учтено общее количество учащихся в каждой из школ. Если известно, что в школе №1 учится 490 детей, а в школе №2 – 1240, то можно определить долю (или процент) близоруких детей в каждой из школ и сравнить их:
в школе №1:  , в школе №2:
, в школе №2:  .
.
Затем следует рассчитать достоверность их различия и сделать вывод – он получится противоположным. Только относительность числа поможет в данном случае правильно определить и сопоставить количество близоруких детей в школах.
При эколого-гигиенических исследованиях состояния окружающей среды возможно использование относительных чисел распределения. Рассмотрим на примере. В летнее время из 120 проб воздуха в 109 пробах были обнаружены концентрации оксида углерода (СО) от 0 до 0,09 мг/м3, в 11 пробах - от 0,1 до 0,15 мг/м3. В зимнее время из 234 проб воздуха в 89 концентрация оксида углерода (СО) составила от 0 до 0,09 мг/м3, в 143 пробах – от 0,1 до 0,5 мг/м3, в 2 пробах – выше 0,5 мг/м3. Необходимо определить, когда воздух был менее загрязнен оксидом углерода, (преобладали пробы с концентрацией газа до 0,09 мг/м3). Соответствующие экстенсивные отношения равны:
|
|
|
| I | 
| II | 
|

| 
| ||

| |||
| Итого: 100% | Итого: 100% |
Вывод: сравнение показателей позволяет сделать вывод об относительном преобладании проб с концентрациями оксида углерода (СО) до 0,09 мг/м3 (90,8%) в летний период по сравнению с зимним (38,3%).
Задания для самостоятельной работы
В ходе диспансеризации начальные стадии искривления позвоночника в школе № 5 обнаружили у 43 школьников из 320 детей, а в школе №9 из 900 – 91. Сравните эти показатели и выясните, отличаются ли данные школы по распространенности начальных этапов искривления позвоночника.
Корреляционный анализ
Для выявления причинно–следственных связей и роли отдельных факторов в формировании здоровья детей и подростков используется корреляционный анализ. При этом для статистической обработки используются данные по двум признакам: факториальному или зависящему от действия какого–либо экологического фактора (причина) и результативному (следствие). Факториальный признак обозначают х–факториальный (фактор риска или их сочетание), результативный признак обозначают у–результативный (показатель состояния здоровья, совокупность состояния показателей здоровья, интегральный индекс здоровья). При корреляционной связи изменение какого–либо признака связано, главным образом, но не исключительно, с изменениями другого признака. Вычисление коэффициента корреляции позволит установить количественную меру этой связи, оценить степень тесноты и определить ее форму. В медицине слабой считается связь при коэффициенте корреляции не выше 0,3, средней от 0,31 до 0,69, сильной от 0,70 до 0,99 (таблица 4). Коэффициенты корреляции равные 1,0 свидетельствуют о функциональной форме связи между изучаемыми явлениями или признаками (функциональная связь отражает строгую зависимость процессов или явлений).
|
|
|
| Таблица 4 | ||
| Оценка коэффициента корреляции | ||
| Корреляция | Коэффициент корреляции | |
| прямая связь | обратная связь | |
| Малая (слабая, низкая) | 0 – 0,30 | 0 – (-0,30) |
| Средняя (умеренная) | 0,31 – 0,69 | (-0,31) – (-0,69) |
| Большая (сильная, высокая) | 0,70 – 0,99 | (-0,70) – (-0,99) |
Примечание: нецелесообразно вычислять коэффициент корреляции при числе контролируемых пар меньше четырех.
Например: необходимо установить, влияет ли уровень освещенности в учебных помещениях на нарушения остроты зрения у школьников. Данные представлены в таблице 5, где Vx – освещенность в люксах, Vy – частота нарушений остроты зрения на 100 детей.
| Таблица 5 | |||||||
| Методика вычисления коэффициента корреляции | |||||||
| № | Vx | Vy | Отклонение от средней | Отклонение в квадрате | Произведения отклонений, xy | ||
| x = (Vx - Mx) | y = (Vy - My) | x ² | y ² | ||||
| 5,1 | - 3,97 | 15,76 | - 496,25 | ||||
| 5,5 | - 3,57 | 12,74 | - 267,75 | ||||
| 7,0 | - 2,07 | 4,29 | - 51,75 | ||||
| 9,3 | - 25 | 0,23 | 0,05 | - 5,75 | |||
| 12,5 | - 75 | 3,43 | 11,76 | - 257,25 | |||
| 15,0 | - 125 | 5,93 | 35,17 | - 741,25 | |||
| Сумма | ∑ Vx = 1650 | ∑ Vy = 54,4 | ∑ x ² = 43750 | ∑ y ² = 79,77 | ∑ xy ² = -1820 |
Решение: Определяем среднюю величину каждого ряда:
 ,
,
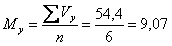 .
.
Вычисляем отклонения каждого значения ряда от средней величины (x и y). Возводим отклонения в квадрат и получаем их суммы: ∑ x ² и ∑ y ². Умножаем отклонения каждого из значений одного ряда на отклонение соответствующего значения другого ряда и находим их сумму: ∑ xy ².
Все полученные значения подставляем в формулу:
 .
.
Прежде, чем делать вывод о наличии или отсутствии связи между этими показателями, определим достоверность полученного коэффициента корреляции. Для этого находим ошибку репрезентативности:

и достоверность
 .
.
Вывод: результат достоверен при любой степени вероятности, следовательно, между уровнем освещенности и нарушением остроты зрения существует обратная тесная связь: с увеличением освещенности частота нарушений остроты зрения уменьшается
| Таблица 6 | |
| Основные показатели, исчисляемые по данным медицинских осмотров | |
| Показатель | Методика вычисления |
| Полнота охвата медицинскими осмотрами, % | (число осмотренных лиц/ число лиц, подлежащих осмотру)*100% |
| Распределение лиц по группам здоровья (I, II, III, IV, V группы), % | (число лиц, отнесенных к данной группе здоровья/ общее число осмотренных)*100% |
| Контингент больных лиц (III – V группы здоровья), % | (число лиц, страдающих теми или иными заболеваниями/ общее число осмотренных)*100% |
| Распространенность данного заболеваия, % | (число лиц, у которых обнаружено данное заболевание/ общее число осмотренных)*100% |
| Частота впервые выявленных заболеваний, % | (число лиц, у которых данное заболевание выявлено впервые/ общее число осмотренных)*100% |
| Структура хронических заболеваний (удельный вес каждого заболевания среди всех хронических заболеваний, принятых за 100%) | (число установленных диагнозов по данному заболеванию/ число всех хронических заболеваний)*100% |
| Таблица 7 | |
| Основные показатели острой заболеваемости (с временной утратой трудоспособности) | |
| Показатель | Методика вычисления |
| Частота заболеваний: а) случаев заболеваний (нетрудоспособности) на 100 детей или подростков | (абсолютное число заболеваний за отчетный период/ средняя численность контингента за отчетный период)*100% |
| б) дней болезни (нетрудоспособности) на 100 детей или подростков | (абсолютное число дней болезни за отчетный период/ средняя численность контингента за отчетный период)*100% |
| в) индекс здоровья | (число детей ни разу не болевших в течение года/ средняя численность контингента за год)*100% |
| г) показатель часто и длительно болевших детей* | (число детей часто и длительно болевших в течение года/ средняя численность контингента за год)*100% |
| Специальные показатели частоты (подгрупповые), по возрасту, полу, типам учреждений и отдельным заболеваниям | (абсолютное число случаев (дней) болезни детей дошкольного (школьного) возраста/ средняя численность детей данного возраста)*100% |
| Длителность случая болезни | (абсолютное число дней болезни за отчетный период/ абсолютное число случаев болезни за отчетный период)*100% |
| Структура заболеваемости (определяется по случаям и дням болезни) | (число случаев (дней) болезни)/ общее число случаев (дней) болезни)*100% |
*Часто болеющими считаются дети, которые болели в течение года 4 и более раз;
|
|
|
“Экстенсивные показатели заболеваемости и их использование
в эколого–медицинских исследованиях.”
|
|
|
При изучении заболеваемости в коллективе используют экстенсивные показатели заболеваемости, к которым относятся индекс здоровья, количество часто болеющих, распределение по группам здоровья.
Индекс здоровья, как и другие экстенсивные показатели, можно использовать при изучении и сравнении заболеваемости детей, обучающихся в различных условиях, например, в школах с углубленным изучением иностранного языка и с углубленным изучением математики и др.
В качестве примера приводим следующие материалы: изучается индекс здоровья (число детей, не болевших в течение года) учащихся первых классов. Полученные для анализа заболеваемости данные приведены в таблице №28.
| Таблица 28 | ||||||
| Индекс здоровья первоклассников за 2006 год | ||||||
| Возраст, лет | Количество обследованных | Количество не болевших | ||||
| мальчики | девочки | мальчики | девочки | |||
| абсолютное | % | абсолютное | % | |||
| 26,6 | ||||||
| 36,6 | 39,1 | |||||
| 7–8 | 56,6 | 65,7 |
Анализ и сравнение полученных данных проводят с учетом достоверности различий сопоставляемых показателей.
С этой целью рассчитывают среднюю ошибку показателя (±m):
 , где
, где
· P – величина показателя заболеваемости, выраженная на 100 человек или 1000 человек в %,
· g – величина, обратная показателю P (g = 100 - P или g = 1000 - P),
· n – число наблюдений (при n ≥30), если n <30, тогда n - 1.
Если утроенная средняя ошибка превышает показатель, то он считается статистически недостоверным и дальнейшей обработке не подлежит:
 ,
,
утроенная средняя ошибка составляет 15,17.
 ,
,
утроенная средняя ошибка составляет 13,70.
Вывод: обе утроенные ошибки не превышают показатели не болевших мальчиков и девочек и могут считаться достоверными
Практическая работа
|
|
|


