Угол между прямыми. Паралельность плоскостей.

Корень n –й степени. Действия с корнями четной и нечетной степени.

В 8 кл. уч-ся изучали понятие корня квадратного из числа. Это понятие вспоминается и по аналогии дается опред. корня n –й степени. Определ 1. Квадрат. корнем из числа а наз. число t, квадрат кот. равен а. . Например, 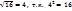. Опред. 2. Корнем n- й степени из числа а наз.такое число t, n- я степень кот. равна а, т.е.

Обращ-ся внимание на то, что сущ-ет единств. корень нечетн. степени из числа а и 2 корня четной степени из любого полож. числа. .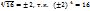

Неотрицат.корень n- й степени из числа а наз арифметич. корнем n- й степени из числа а. – арифметический корень 4-й степени. - радикал.

В современ. уч. пособиях сначала рассм-ся общие св-ва для корня n –й степени(справедливые для n – четн. и n- нечетн.). Теорема 1. Пусть n- нечет. число, тогда корень n –й степени из . Теорема 2. Если n- четное число, то при любом знач. а верно рав-во: .Пример. , (m . =m. .

= n.

Теорема 3. Пусть n, k- натур. числа,тогда при любом нетриц. значении а верны рав-ва: 1) , . 2) =, . =, 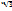. Теорема 4. Пусть к – целое число, тогда при любом положении а верно рав-во: = . =

Действия с корнями нечетной степени.

Терема. Пусть n – нечетн. число, тогда: 1) = . 2) = . 3) При любых знач-ях a и b верно рав- во: = .

Если n – нечет. число, то справедливо рав-во: а) = * *… * 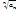. б) = , а R. = .

Преобразования вида:: = наз. вынесением множителя из под знака корня нечетной степени.Преобразования наз внесением множителя под знак корня нечет. степени.

Действия с корнями четной степени.

Теорема. Пусть n- четное число, тогда: 1) Для любых неотриц. значений a и b верно рав- во:1) . 2) Для люб. неотриц-х значений а и положит-х значений b верно рав-во: . 3) При любых значениях а и неотриц-х значениях b верно рав-во: = .

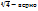= * , = * – не верно.

Пусть n – четное число, тогда для любых неотриц-х справедливо рав-во: = * *… * . Если положить = , то . Пример. Внести множитель под знак корня m , m m = - (- m) = - = - .

y , y . y

3. Перпендик. Прямой и плос-ти. Прямая, пересек. плос-ть наз. ┴ к плос-ти, если она ┴ кажд. прямой, лежащ. в этой плос-ти.

Т-ма 1: если одна из 2-х ‖‖ прямых ┴ 3-ей прямой, то и др. прямая ┴ этой прямой.

a‖b, a┴c следов. b┴c.

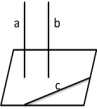
Т-ма 2: если одна из 2-х ‖‖ прямых ┴ плос-ти, то и др. прямая ┴ этой плос-ти.

 

a‖b, a┴ следов. b┴ .

Т-ма 3: если 2 прямые ┴ одной плос-ти, то они ‖.

a┴ , b┴ , следов.a‖b

Т-ма 4 (признак ┴-ти прямой и плос-ти): если прямая ┴ 2-м пересекающ. прямым, лежащим в плос-ти, то она ┴ этой плос-ти.

Док-во: 1. Рассм. случай, когда прямая а проходит через т. О (т. пересеч.) прям. р и q. Восп. опред. ┴-ти прямой и плос-ти.Для этого нужно док-ть, что прямая а┴ любой прямой (произв.) l в плос-ти . Через т. О провед. прям. l₁‖l. На прям. а отметим т. А и В, так чтобы т. О была середин. отрезка АВ. В плос-ти провед. произвольн. прям., т. о. чтобы она пересек. прямые pql₁. Т. пересеч. наз. P,Q,L. Соед. P,Q,L с т. А.

∆АОР=∆ВОР как прямоугольн. по 2-м катетам. a┴p и a┴q. Из рав-ва след., что AP=BP(*). Анал., ∆AOQ=∆BOQ (как прямоуг. по 2-м катетам) следов. AQ=BQ(**)

∆APQ=∆BPQ, т.к. AP=PB, AQ=BQ и PQ-общая (по 3-м сторонам). Из рав-ва ∆, следует рав-во углов <APL=<BPL.

∆APL=∆BPL по 2-м сторонам и углу между ними (AP=BP, PL- общая, угол <APL=<BPL). Из рав-ва ∆ следует, что AL=BL, т. е. ∆ALB равнобедрен. LO-медиана этого ∆,следов. LO- высота, т.е. AB┴LO,следов. а┴l₁. По опр. прям. а┴ плос-ти . На основании т-мы 1 можно сдел. вывод, что а┴l.

2. Если прям. не прох. через т. О, тогда провед. через т. О прям. l₁‖a. Тогда, по т-ме 1 a₁┴p, a₁┴q, a₁┴ . По т-ме 2 прямая а┴

Т-ма 7: квадрат длины диагонали прямоуг. параллепип. = сумме квадратов 3-х его ребер, имеющ. общую вершину.d²=a²+b²+c²

Угол между прямыми. Паралельность плоскостей.

Любые 2 пересек-ся прямые лежат в одной пл-ти и образуют 4 неразвернутых угла.

За угол между прямыми выбир. наименший из этих углов. Если прямые не лежат в одной пл-ти, то они скрещивающиеся. ОПР: угол между скрещивающимися прямыми а и в наз угол между построенными пересек. прямыми а₁ и в₁

Две пл-ти наз параллельными, если они не пересекаются.

ТЕОР 1: Признак параллельности пл-тей Если 2 пересек-ся прямые одной пл-ти соотв. параллельны двум прямым другой пл-ти, то эти пл-ти параллельны.

Дано: аǁb, bǁb₁, О=а∩b. Док-ть:αǁβ

Док-во: по признаку параллельности прямой и пл-ти αǁβ и bǁβ. Предположим, что α и β не параллельны. => они пересекаются по прямой c. Тогда пл-ть α проходит через прямую а, кот. ǁ пл-ти β и пересекает пл-ть β по прямой c. Аналогично пл-ть α проходит через прямую bǁβ и перес. ее по прямой c. Значит bǁc. Т.о. через точку О проходят 2 прямые а и bǁс. Это противоречит теореме о том, что через точку О проходит единств. прямая ǁ прямой с.

ТЕОР 2:О прямых пересеч 2-х ǁ пл-тей 3-ей пл-тью. Если 2 ǁпл-ти пересечены третьей, то прямые их пересечения ǁмежду собой.

Поделиться:

Воспользуйтесь поиском по сайту: