 |
Оценка значимости параметров линейной регрессии
|
|
|
|
Критерии качества модели: коэффициент детерминации и статистика Фишера.
Коэффициент детерминации
Для линейной модели он совпадает с квадратом коэффициента корреляции, но пригоден и для нелинейных моделей. На Рисунке 3.2. показана аппроксимация параболой. Коэффициент корреляции близок к нулю, а коэффициент детерминации – к единице, так как дисперсия Рис.3.2.
остатков существенно меньше дисперсии Y. Это говорит о высоком качестве модели.
Формула (3.1) легко преобразуется
(3.2)
где ДИСП – функция Excel Дисперсия. Вообще говоря, несмещённой оценкой дисперсии остатков парной регрессии является
но функция ДИСП.В делит на (n-1), и в данном случае всё получается правильно. В данном случае R 2 = 0,854, что соответствует коэффициенту корреляции 0,924, то есть имеет место сильное влияние переменной X на Y.
Дисперсия суммы двух независимых переменных равна сумме их дисперсий. В Таблице вы видите, что ДИСП(Y)=ДИСП(Ŷ ) + ДИСП(е).
Надо сказать, что S(Y – Ycp)2 обозначают TSS (Total Squared Sum); в российских учебниках S(Ŷ – Ŷcp)2 обозначают RSS, а Sе2 ESS (Error Squared Sum; в английских учебниках S(Ŷ – Ŷcp)2 обозначают ESS (Explained Squared Sum) а Sе2 RSS (Residual Squared Sum). Поэтому мы не будем пользоваться этими обозначениями.
Оценка значимости уравнения регрессии в целом даётся с помощью F -критерия Фишера. При этом проверяется нулевая гипотеза, что коэффициент регрессии b равен нулю и, следовательно, фактор X не оказывает влияния на результат Y. Давно составлены таблицы критических значений F -статистики в зависимости от числа измерений n, числа степеней свободы, или количества независимых переменных m и уровня значимости a.
Статистика Фишера равна частному от деления дисперсии Ŷ, или факторной дисперсии, и дисперсии остатков, вычисленных с учётом числа степеней свободы: 1 для Ŷ и n-2 для остатков.
|
|
|
Для множественной регрессии и полиномиальной, которую можно преобразовать в множественную, число степеней свободы Ŷ равно числу независимых переменных m, а число степеней свободы остатков равно n-m-1. Статистику Фишера удобно вычислять через коэффициент детерминации:
(3.3)
Чем больше статистика Фишера, тем лучше прогнозы, сделанные с использованием модели. Из формулы (3.3) следует, что F возрастает с ростом R 2 и числа измерений, но уменьшается при увеличении числа влияющих переменных, то есть надо аккуратно подходить к включению в модель новых влияющих переменных, а также не использовать для аппроксимации полиномы высоких степеней. Полезно помнить, что при уровне значимости a=0,05, то есть при доверительной вероятности 95% и количестве замеров более 15 критическое значение F для парной регрессии около 4,2, а при m=4 около 3. Начиная с этих значений F можно говорить о существовании влияния регрессоров на эндогенную переменную. Таблицы критических значений F есть во всех книгах по мат.статистике и эконометрике, поэтому в этой книге они не приводятся. Их можно вычислить в Excel с помощью функции FРАСПОБР с аргументами: уровень значимости (здесь a=0,05); число регрессоров m; N-m-1; где N число измерений.
Коэффициенты линейного уравнения регрессии bi имеют экономический смысл: это предельные функции, или производные эндогенной переменной по влияющим:
В случае парной регрессии это однозначно, в множественной регрессии всё сложнее из-за взаимного влияния регрессоров.
Для оценки погрешностей коэффициентов уравнения парной линейной регрессии Ŷ = a + bx используются выражения
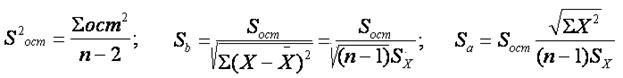где S – выборочные оценки стандартных отклонений s. Для принятия гипотезы о влиянии регрессора на эндогенную переменную используются таблицы критических значений t -статистики Стьюдента. Для bt=b/Sb. Предполагается, что при числе измерений больше 20 истинные значения коэффициентов уравнения регрессии a и b лежат в интервалах {a-2Sa, b+2 Sb } и {b-2Sb, b+2 Sa } с доверительной вероятностью 95%.
|
|
|
Матричный метод МНК
Матричный метод МНКоснован на представлении множеств X, Y, остатков E и параметров линейной модели B в виде векторов, над которыми затем проводятся операции. Векторное представление модели
Y = B * X + E
где
Y B X E
y1 1 x1 e1
y2 1 x2 e2
. a..
. b..
...
yn 1 xn en
Эту модель, записанную в векторном виде или в виде системы линейных уравнений, называют схемой Гаусса-Маркова.
Условие МНК S e 2 -> min, или в матричном виде (Y-XB)T(Y-XB) -> min.
Т означает транспонирование, то есть преобразование столбца в строку. Решением является вектор В:
B = (XTX)-1XTY
Здесь -1 означает обращение матрицы. Транспонирование и обращение матриц можно выполнять в Excel, используя функции ТРАНСП и МОБР.
Теорема Гаусса-Маркова
Согласно теореме Гаусса-Маркова, Метод наименьших квадратов, приведённый к линейному преобразованию матриц или к системе линейных уравнений, обеспечивает наилучшую несмещенную, эффективную и сходящуюся к пределу (“состоятельную”) оценку вектора параметров, т.е. наилучшее качество линейной модели, если соблюдаются условия (по [ 1 ]):
1. Линейная модель соответствует действительности.
2. Существует дисперсия регрессора.
3. Математическое ожидание возмущения равно нулю: E(ui) = 0.
4. Возмущение имеет нормальное распределение.
5. Равенство ожидаемых значений дисперсий возмущений в разных диапазонах Х: E(u2) = Const. Это свойство называется гомоскедастичность, его несоблюдние – гетероскедастичность. Отклонение от гомоскедастичности проверяется по тесту Голдфелда-Квандта
GQ = Se12/Se22
где Se12 и Se22 – суммы квадратов остатков (отклонений) в первой и последней трети (или в половинах) диапазона Х; большая сумма делится на меньшую!!!;GQ сравнивают с критерием Фишера для заданных уровня значимости и количества измерений; гипотеза о гомоскедастичности принимается при GQ <4,35.
6. Отсутствие автокорреляции, т.е. взаимозависимости возмущений. Её оценивают, вычисляя статистикуДарбина-Уотсона остатков е:
для которой вычислены критические значения при различных уровнях значимости и числе измерений. Приблизительно DW =0…1 означает положительную автокорреляцию, 3…4 отрицательную автокорреляцию, DW =1,5…2,5 позволяет принять гипотезу об отсутствии автокорреляции, DW =1…1,5 и DW =2,5…3 не позволяют принять гипотезу о наличии или отсутствии автокорреляции. Наличие автокорреляции означает, что аппроксимирующая функция подобрана неверно, или же требуется применение других методов и моделей. Автокорреляция разобрана в главе 8.
|
|
|
Статистику Дарбина-Уотсона можно вычислить по формуле
DW = 2(1-Rавт),
где Rавт - коффициент автокорреляции, вычисляемый с помощью функции КОРРЕЛ: задать в окне Массив1 диапазон остатков с номерами 1: n- 1, а в окне Массив2 диапазон 2: n.
Понятия “гетероскедастичность” и “автокорреляция” актуальны, если массивы данных упорядочены, что имеет место для временных рядов. “Пространственные” данные можно искусственно упорядочить, например, отсортировав их по возрастанию какой-либо переменной; при этом можно выявить кластеры с аномальной дисперсией остатков, что может означать неоднородность выборки или неадекватность модели.
Считается, что гетероскедастичность может привести к снижению эффективности оценок коэффициентов, и надо её искусственно подавлять: делить остатки в таблице 3.3 на их стандартные отклонения в диапазонах, а затем минимизировать сумму их квадратов. Эта технология называется Взвешенный метод наименьших квадратов (ВМНК) и обычно используется в матричном варианте МНК (раздел 3.3). При обнаружении автокорреляции остатков применяется Обобщённый метод наименьших квадратов ОМНК, основанный на преобразовании матриц, но с учётом корреляций остатков.
Целесообразность применения ВМНК и ОМНК обсуждается в разделе 5.1.
Контрольные вопросы.
1. Общий вид уравнений парной и множественной регрессии.
2. Нелинейные уравнения регрессии.
3. Формулы для вычисления коэффициентов парной линейной регрессии и их погрешностей.
4. Метод наименьших квадратов (МНК) и система нормальных уравнений парной линейной регрессии.
|
|
|
5. Схема Гаусса-Маркова и Матричный метод МНК.
6. Теорема Гаусса-Маркова: формулировка и условия.
7. Показатели качества эконометрической модели: коэффициент детерминации R2, статистика Фишера F, t -статистики Стьюдента для коэффициентов уравнений.
8. Показатели качества эконометрической модели: тест Дарбина-Уотсона на автокорреляцию DW, тест Голдфелда-Квандта на гетероскедастичность GQ.
9. Гетероскедастичность случайного возмущения. Причины, последствия.
10. Что такое ВМНК и ОМНК, и когда они применяется.
|
|
|
