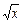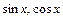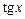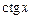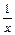|
Аналитическая геометрия на плоскости. Прямая на плоскости
|
|
|
|
Вологодский государственный технический университет
(Череповецкий филиал)
Кафедра социально-гуманитарных и естественно-научных дисциплин
МАТЕМАТИКА
Учебно-методическое пособие
По подготовке к контрольной работе
Для студентов очной и заочной формы обучения
(по сокращенным программам)
I часть
Специальность 151001 (120100) – Технология машиностроения
Череповец
2007
УДК
Математика: Учебно-методическое пособие по подготовке к контрольной работе для студентов очной и заочной формы обучения (по сокращенным программам) I часть. – Череповец: ВоГТУ, 2007. – 87 с.
Учебно-методическое пособие содержит краткую теорию по определенным разделам математики, пример решения варианта контрольной работы, задачи для контрольных заданий, список литературы.
Пособие предназначено для студентов очной и заочной формы обучения по сокращенным программам специальности 151001 (120100) – Технология машиностроения.
Утверждено редакционно-издательским советом ВоГТУ
Составитель Русина Л.Г., кандидат технических наук, доцент кафедры СГиЕНД
Рецензент Толстиков А.В., кандидат физико-математических наук, профессор кафедры алгебры и геометрии ЧГУ.
Содержание
Глава I. Элементы линейной алгебры.. 4
§ 1. Матрицы и действия с ними. 4
§ 2. Определители и их вычисление. 5
§ 3. Решение систем линейных уравнений. 6
Глава II. Элементы векторной алгебры и аналитической геометрии. 8
§ 1. Векторы. Основные понятия. 8
§ 2. Скалярное произведение векторов. 9
§ 3. Векторное произведение векторов. 10
§ 4. Смешанное произведение векторов. 11
§ 5. Аналитическая геометрия на плоскости. Прямая на плоскости. 11
|
|
|
§ 6. Аналитическая геометрия в пространстве. 13
п.1 Плоскость. 13
п.2 Прямая в пространстве. 14
Глава III. Элементы математического анализа. 15
§ 1. Кванторы.. 15
§ 2. Определение функций. 15
§ 3. Предел функции  , непрерывность, точки разрыва. 16
, непрерывность, точки разрыва. 16
§ 4. Производная функции одной переменной. 20
§ 5. План полного исследования функции. 22
§ 6. Частные производные функции нескольких переменных.Производная сложной функции нескольких переменных. 24
§ 7. Наибольшее и наименьшее значения функции. 26
§ 8. Неопределенный интеграл. 27
§ 9. Определенный интеграл. 31
§ 10. Приложения определенных интегралов. 32
Глава IV. Пример решения варианта контрольной работы.. 34
Глава V. Задачи для контрольных заданий. 54
Введение
Одной из важнейших задач учебного процесса высшего учебного заведения является развитие у обучаемых навыков самостоятельной работы по нахождению, изучению и по применению научно-технической информации.
Настоящее пособие предназначено для студентов инженерных специальностей очной и заочной формы обучения. Оно составлено в соответствии с программой по математике для факультета «Технология машиностроения».
Пособие служит руководством для студентов при самостоятельном выполнении контрольных заданий, запланированных в I учебном семестре. Пособие начинается с краткого теоретического материала по разделам математики:
«Элементы линейной алгебры»,
«Элементы векторной алгебры и аналитической геометрии»,
«Элементы математического анализа».
Затем приводится конкретный пример решения варианта контрольной работы и предлагаются задачи для контрольных заданий.
Глава I. Элементы линейной алгебры
§ 1. Матрицы и действия с ними
Определение. Матрицей размерности  называют прямоугольную таблицу чисел:
называют прямоугольную таблицу чисел:
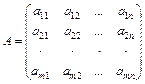 ,
,
где  – элементы матрицы,
– элементы матрицы,
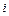 – номер строки,
– номер строки,  ,
,
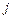 – номер столбца,
– номер столбца,  .
.
Если  , то матрицу называют квадратной n -го порядка.
, то матрицу называют квадратной n -го порядка.
|
|
|
Определение. Матрицу n -го порядка, в которой
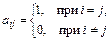 называют единичной.
называют единичной.
Например, единичная матрица 4-го порядка:
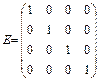
Определение. Матрицу 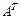 , получаемую из матрицы А заменой строк и столбцов друг на друга, называют транспонированной.
, получаемую из матрицы А заменой строк и столбцов друг на друга, называют транспонированной.
Например, если  , то
, то  .
.
1. Любую матрицу можно умножить на любое действительное число  :
:  .
.
2. Матрицы одной и той же размерности можно складывать (вычитать):

3. Матрицу А можно умножать на матрицу В только, если число столбцов матрицы А равно числу строк матрицы В:
 ,
,
причем элементы матрицы С находятся по правилу:
 ,
,
то есть элементы i – ой строки матрицы А умножаются на соответствующие элементы j –го столбца матрицы В и полученные произведения складываются.
§ 2. Определители и их вычисление.
Каждой квадратной матрице по определенному правилу ставится в соответствие число, называемое определителем.
1. Правило вычисления определителя 2-го порядка:

2. Правило вычисления определителя 3-го порядка – правило треугольников:
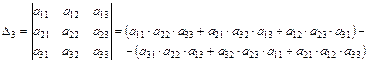
Правило разложения определителя по элементам 1-й строки:
 , где алгебраические дополнения
, где алгебраические дополнения  , а минор
, а минор  – определитель, получающийся из данного путем вычеркивания i -ой строки и j -го столбца.
– определитель, получающийся из данного путем вычеркивания i -ой строки и j -го столбца.
Таким образом,

Аналогично определитель можно раскладывать по элементам любой строки или столбца.
3. Правило вычисления определителя n –го порядка. Определители n –го порядка вычисляются также разложением по элементам любой строки или столбца.
Таким образом,
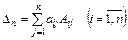 – разложение определителя по элементам i –ой строки
– разложение определителя по элементам i –ой строки
или
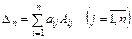 – разложение определителя по элементам j –го столбца
– разложение определителя по элементам j –го столбца
§ 3. Решение систем линейных уравнений
1. Формулы Крамера для решения систем трех линейных уравнений с тремя неизвестными:
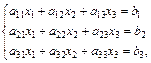
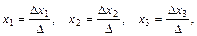
где


2. Метод Гаусса.
Сущность метода состоит в том, что посредством последовательных исключений неизвестных, данная система преобразуется в систему ей эквивалентную. Последовательное исключение неизвестных осуществляется с помощью элементарных преобразований системы:
а) перестановок двух любых уравнений;
б) умножений обеих частей одного из уравнений на любое, отличное от нуля число;
в) прибавление к обеим частям одного из уравнений соответствующих частей другого, умноженных на любое число.
|
|
|
Заметим, что удобно работать не с самими уравнениями системы, а с ее расширенной матрицей.
Пример.

Переставим местами два первых уравнения
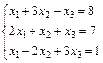
Составим расширенную матрицу системы

Первую строку умножим на «–2» и сложим со второй строкой.
Первую строку умножим на «–1» и сложим с третьей строкой.
Получаем матрицу:

Вторую строку умножим на «–1» и сложим с третьей:
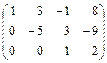
Этой матрице соответствует система уравнений:
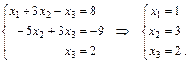
Глава II. Элементы векторной алгебры и аналитической геометрии
§ 1. Векторы. Основные понятия
 |
Вектор – направленный отрезок (рис.1).
Рис. 1  Если точка
Если точка 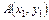 – начало вектора, точка
– начало вектора, точка  – конец вектора, то координаты вектора
– конец вектора, то координаты вектора 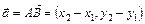 .
.
Вектор 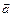 записывают также через единичные Рис. 1
записывают также через единичные Рис. 1
векторы осей  :
: 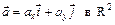 (на плоскости) (рис. 2),
(на плоскости) (рис. 2), 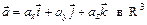 (в пространстве).
(в пространстве).
Пусть 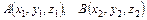 , тогда
, тогда
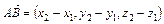 . (1)
. (1)
Расстояние между точками  и
и  :
:
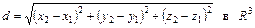 (2)
(2)
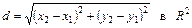 (2')
(2')
Координаты точки С, являющейся серединой отрезка АВ:
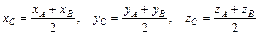 (3)
(3)
Длина вектора 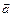 :
: 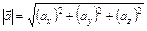 (4)
(4)
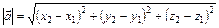 (4')
(4')
§ 2. Скалярное произведение векторов
Определение. 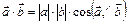 . (5)
. (5)
Если  , то
, то
 (6)
(6)
Из формулы (5) имеем угол между векторами 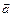 и
и  :
:
 (7)
(7)
Проекция вектора 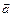 на вектор
на вектор 

Физический смысл скалярного произведения
Пусть материальная точка  движется по прямой от точки
движется по прямой от точки  до точки
до точки  , проходя при этом путь
, проходя при этом путь  .
.
Допустим, что на точку  действует сила
действует сила  , постоянная по величине и направлению и составляющая с направлением перемещения точки угол
, постоянная по величине и направлению и составляющая с направлением перемещения точки угол 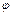 .
.
Из физики известно, что работа  , совершаемая при этом силой
, совершаемая при этом силой  на участке
на участке  равна
равна  , где
, где  , или
, или  .
.
Свойства:
1) 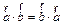 ,
,
2) 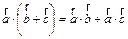 ,
,
3) если 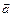
 , то
, то 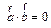
Замечание:
а) 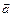 ||
|| 
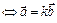 или
или 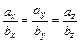 .
.
б) 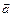

 или
или  .
.
|
|
|
§ 3. Векторное произведение векторов
Определение.  – вектор, удовлетворяющий трем условиям:
– вектор, удовлетворяющий трем условиям:
1)  ,
,
2)  ,
,
3) 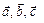 образуют правую тройку, то есть, если смотреть из конца
образуют правую тройку, то есть, если смотреть из конца 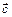 , то кратчайший поворот от
, то кратчайший поворот от  к
к  виден против часовой стрелки (рис. 3).
виден против часовой стрелки (рис. 3).
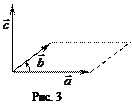 Замечание: Если вектор
Замечание: Если вектор 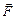 изображает силу, приложенную к точке А, а вектор
изображает силу, приложенную к точке А, а вектор  направлен из некоторой точки О в точку А, то вектор
направлен из некоторой точки О в точку А, то вектор 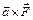 представляет собой момент силы
представляет собой момент силы  относительно точки О:
относительно точки О:  (8)
(8)
Свойства:
1)  ,
,
2)  , если
, если 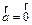 , либо
, либо  , либо
, либо  ||
||  ,
,
3)  ,
,
4)  .
.
Если известны координаты векторов, то
 (9)
(9)
Площадь параллелограмма, построенного на векторах  и
и  :
:
 – площадь треугольника (10)
– площадь треугольника (10)
§ 4. Смешанное произведение векторов
Смешанным произведением векторов  называют число, равное
называют число, равное  . Обозначают также
. Обозначают также 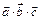 .
.
Если известны координаты векторов, то

Объем пирамиды равен  (11)
(11)
Аналитическая геометрия на плоскости. Прямая на плоскости
Общее уравнение прямой  :
:
 , где
, где 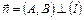 . (12)
. (12)
Уравнение прямой с угловым коэффициентом:
 ,
, 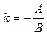 ,
,  ,
, 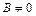 , (13)
, (13)
где  – угловой коэффициент прямой, равный тангенсу угла
– угловой коэффициент прямой, равный тангенсу угла  наклона прямой
наклона прямой  к оси
к оси  ;
;  – отрезок, отсекаемый прямой на оси
– отрезок, отсекаемый прямой на оси  .
.
 – уравнение прямой в отрезках, (14)
– уравнение прямой в отрезках, (14)
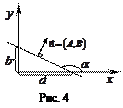 где
где  и
и  – отрезки, отсекаемые прямой на осях
– отрезки, отсекаемые прямой на осях  и
и  соответственно (рис. 4)
соответственно (рис. 4)
Уравнение прямой, проходящей через заданную точку 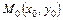 перпендикулярно заданному вектору нормали
перпендикулярно заданному вектору нормали  :
:
 (15)
(15)
Уравнение прямой, проходящей через заданную точку 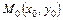 параллельно заданному направляющему вектору
параллельно заданному направляющему вектору  :
:
 (16)
(16)
Уравнение прямой, проходящей через две заданные точки 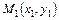 и
и  :
:
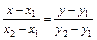 (17)
(17)
Уравнение прямой, проходящей через заданную точку 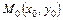 с заданным угловым коэффициентом
с заданным угловым коэффициентом  :
:
 (18)
(18)
Угол 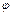 между прямыми
между прямыми  и
и 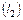
Если  :
: 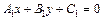
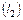 :
:  ,
,
то  (19)
(19)
Если  :
: 

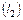 :
: 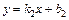 ,
,
то 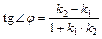 (20)
(20)
Замечание.
а)  ||
|| 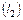
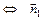 ||
|| 

 или
или 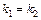 , (21)
, (21)
б) 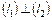
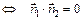

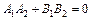 или
или 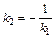 (22)
(22)
Координаты 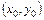 точки пересечения двух прямых
точки пересечения двух прямых  и
и 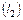 ищутся как решение системы:
ищутся как решение системы:
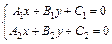 (23)
(23)
Расстояние  от точки
от точки  до прямой
до прямой  :
: 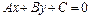 ищется по формуле:
ищется по формуле:
|
|
|
 (24)
(24)
§ 6. Аналитическая геометрия в пространстве
п.1 Плоскость.
Общее уравнение плоскости 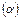 :
:
 , где
, где 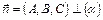 . (25)
. (25)
Уравнение плоскости в отрезках:
 , (26)
, (26)
где 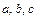 – отрезки отсекаемые плоскостью на координатных осях
– отрезки отсекаемые плоскостью на координатных осях  соответственно.
соответственно.
Уравнение плоскости, проходящей через заданную точку  перпендикулярно заданному вектору нормали
перпендикулярно заданному вектору нормали  :
:
 (27)
(27)
Уравнение плоскости, проходящей через три заданные точки 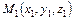 ,
, 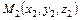 и
и 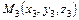 :
:
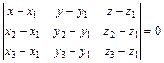 (28)
(28)
Угол 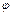 между плоскостями
между плоскостями  и
и 
Если  :
: 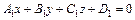
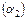 :
:  , то
, то
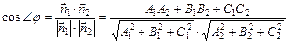 (29)
(29)
Замечание.
а)  ||
|| 
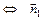 ||
|| 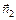

 , (30)
, (30)
б) 


 . (31)
. (31)
Расстояние  от заданной точки
от заданной точки 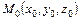 до заданной плоскости
до заданной плоскости 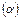 :
:  ищется по формуле:
ищется по формуле:
 (32)
(32)
п.2 Прямая в пространстве.
Уравнение прямой  , проходящей через заданную точку
, проходящей через заданную точку 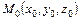 параллельно заданному направляющему вектору
параллельно заданному направляющему вектору 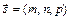 :
:
 – каноническое уравнение прямой, (33)
– каноническое уравнение прямой, (33)
 – параметрические уравнения прямой (34)
– параметрические уравнения прямой (34)
Уравнения прямой, проходящей через две заданные точки 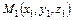 и
и 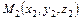 :
:
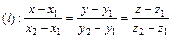 (35)
(35)
Угол между прямыми в пространстве
Если известны направляющие вектора для прямых  и
и 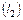 :
:
 то
то

Точка пересечения прямой  и плоскости
и плоскости  ищется как решение системы
ищется как решение системы
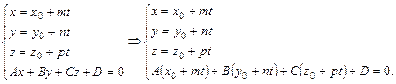 (36)
(36)
Из последнего уравнения (36) находим значения параметра  и, подставляя его в первые три уравнения, находим коорданты точки пересечения прямой и плоскости
и, подставляя его в первые три уравнения, находим коорданты точки пересечения прямой и плоскости
Замечание.
а)  ||
|| 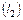
 ||
|| 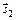
б) 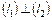
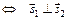
Пусть известны нормаль 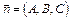 к плоскости и направляющий вектор прямой
к плоскости и направляющий вектор прямой 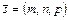 , тогда
, тогда
а)  ||
|| 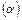
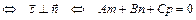 , (37)
, (37)
б)  ||
||  (38)
(38)
в)  (39)
(39)
Глава III. Элементы математического анализа
§ 1. Кванторы
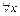 – «для любого
– «для любого  » – квантор всеобщности,
» – квантор всеобщности,
 – «существует
– «существует  такое, что …» – квантор существования,
такое, что …» – квантор существования,
 – «существует только одно
– «существует только одно  такое, что …» – квантор существования и единственности.
такое, что …» – квантор существования и единственности.
§ 2. Определение функций
Определение. Если каждому числу  поставлено в соответствие по некоторому правилу
поставлено в соответствие по некоторому правилу 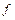 вполне определенное действительное число
вполне определенное действительное число  , то говорят, что на множестве
, то говорят, что на множестве  определена числовая функция
определена числовая функция 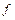 , т.е.
, т.е. 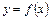 .
.
Множество  называют областью определения функции и обозначают
называют областью определения функции и обозначают  .
.
Определение. Если каждой паре 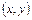 значений двух независимых друг от друга величин
значений двух независимых друг от друга величин  и
и  из некоторой области
из некоторой области  соответствует определенное значение величины
соответствует определенное значение величины  , то говорят, что
, то говорят, что  есть функция двух независимых переменных
есть функция двух независимых переменных  и
и  , определенная в области
, определенная в области  , т.е.
, т.е.

Область  при этом называется областью определения функции
при этом называется областью определения функции 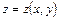 .
.
При нахождении области определения функции двух переменных следует учитывать свойства элементарных функций.
| Функция | Область определения | ||
| 1. |
| 
| |
| 2. |
| 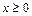
| |
| 3. |
| 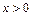
| |
| 4. |
| 
| |
| 5. |
| 
| |
| 6. |
| 
| |
| 7. |
| 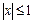
| |
| 8. |
| 
| |
§ 3. Предел функции 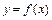 , непрерывность, точки разрыва
, непрерывность, точки разрыва
Рассмотрим
 – «
– «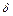 »–окрестность точки
»–окрестность точки 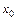 ,
,
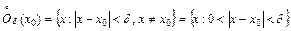 – выколотую «
– выколотую «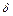 »– окрестность точки
»– окрестность точки  .
.
Определение (по Коши): Число 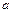 называется пределом функции
называется пределом функции 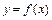 в точке
в точке  (или при
(или при  ), если для любого
), если для любого 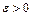 существует такое число
существует такое число 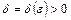 , что для всех
, что для всех  , удовлетворяющих условию
, удовлетворяющих условию 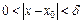 выполняется неравенство:
выполняется неравенство:  .
.
 .
.

 – Первый замечательный предел
– Первый замечательный предел
 (40)
(40)
 – Второй замечательный предел
– Второй замечательный предел
Таблица эквивалентностей при 
 ,
, 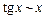 ,
,  ,
,  ,
, 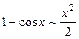 ,
,  ,
,  ,
, 
К неопределенностям относятся выражения вида  ,
,  ,
,  ,
, 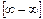 ,
,  и др.
и др.
1.  . Чтобы раскрыть неопределенность этого вида необходимо в числителе и знаменателе дроби выделить сомножитель, обращающий их в ноль и сократить на него дробь. Способы выделения сомножителя зависят от вида функции, например,
. Чтобы раскрыть неопределенность этого вида необходимо в числителе и знаменателе дроби выделить сомножитель, обращающий их в ноль и сократить на него дробь. Способы выделения сомножителя зависят от вида функции, например,
а) 
б) 

Можно также пользоваться таблицей эквивалентностей.
в) 

2.  . Чтобы раскрыть неопределенность вида
. Чтобы раскрыть неопределенность вида  можно пользоваться эквивалентными бесконечно большими, например,
можно пользоваться эквивалентными бесконечно большими, например,


3. Неопределенности вида 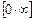 и
и 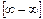 сводятся предварительно к неопределенностям вида
сводятся предварительно к неопределенностям вида  или
или  , например,
, например,
а) 

б) 



4. Неопределенность вида  раскрывается с помощью второго замечательного предела. Например,
раскрывается с помощью второго замечательного предела. Например,

 .
.
Определение. Функцию 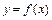 называют непрерывной в точке
называют непрерывной в точке 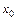 , если выполняются следующие три условия:
, если выполняются следующие три условия:
1) 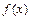 определена в точке
определена в точке 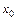 , то есть
, то есть 
2) существует  ,
,
3) 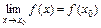
1. Если в точке 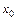 существуют конечные односторонние пределы и
существуют конечные односторонние пределы и  или
или  , то точку
, то точку 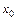 называют точкой разрыва I рода, устранимого.
называют точкой разрыва I рода, устранимого.
2. Если в точке 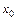 существуют конечные односторонние пределы и
существуют конечные односторонние пределы и  , то точку
, то точку  называют точкой разрыва I-го рода, неустранимого.
называют точкой разрыва I-го рода, неустранимого.
3. Если хотя бы один из односторонних пределов равен  или
или 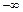 , то точку
, то точку  называют точкой разрыва II рода.
называют точкой разрыва II рода.
Пример:
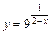
В точке  функция не определена, следовательно,
функция не определена, следовательно,  – точка разрыва.
– точка разрыва.
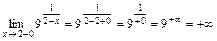 ,
,

Следовательно,