 |
Задачи для самостоятельного решения
|
|
|
|
ДИНАМИКА ТВЕРДОГО ТЕЛА
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________
Краткая теория и методические указания
Твердым телом (ТТ) называется система точек, жестко связанных между собой. Твердым можно считать любое тело, которое при решении задач нецелесообразно моделировать точкой, но форму и объем такого тела можно считать неизменным на протяжении всего времени движения.
Положение ТТ в пространстве полностью определено, если известны положение какой-либо жестко связанной с ним точки и три угла поворота тела вокруг трех взаимно перпендикулярных осей, проходящих через эту точку. Таким образом, положение ТТ определяется шестью независимыми координатами, т. е. имеется 6 степеней свободы (3 поступательные и 3 вращательные).
Обычно движение ТТ рассматривается как поступательное движение центра масс ТТ и вращательное движение вокруг этой точки О. Введем радиус-вектор  – центр масс ТТ. Заметим, что центр масс не обязательно совпадает с какой-либо точкой ТТ. Тогда для центра масс можно записать:
– центр масс ТТ. Заметим, что центр масс не обязательно совпадает с какой-либо точкой ТТ. Тогда для центра масс можно записать:
 (4.1)
(4.1)
Из него видно, что центр масс ТТ движется как материальная точка с массой, равной массе  ТТ, к которой приложена равнодействующая всех внешних сил
ТТ, к которой приложена равнодействующая всех внешних сил  .
.
Допустим, что, решив уравнение (4.1), нашли  . Однако остается неизвестным, как повернуть ТТ вокруг точки O. Для характеристики этого поворота введем момент импульса ТТ:
. Однако остается неизвестным, как повернуть ТТ вокруг точки O. Для характеристики этого поворота введем момент импульса ТТ:  . Для описания вращательного движения вводится уравнение:
. Для описания вращательного движения вводится уравнение:
 (4.2)
(4.2)
где  – сумма моментов внешних сил.
– сумма моментов внешних сил.
Пусть ТТ вращается вокруг оси  с угловой скоростью
с угловой скоростью  . Это значит, что любая точка
. Это значит, что любая точка  (кроме точек, лежащих на оси
(кроме точек, лежащих на оси  ) имеет скорость
) имеет скорость  , тогда как линейные скорости точек ТТ, вообще говоря, различны. Заметим, однако, что все они перпендикулярны оси
, тогда как линейные скорости точек ТТ, вообще говоря, различны. Заметим, однако, что все они перпендикулярны оси 
|
|
|
Проекция момента импульса  на ось
на ось  равна
равна  где
где  – угол между радиусом-вектором
– угол между радиусом-вектором  и осью
и осью  . Введя обозначения
. Введя обозначения  , с учетом
, с учетом  , получим
, получим  Сумма
Сумма  , не зависит от движения ТТ.
, не зависит от движения ТТ.  называется моментом инерции твердого тела относительно оси
называется моментом инерции твердого тела относительно оси  и зависит только от распределения массы в ТТ. Таким образом,
и зависит только от распределения массы в ТТ. Таким образом,  , где
, где  – угловая скорость вращения ТТ вокруг оси
– угловая скорость вращения ТТ вокруг оси 
Поскольку  при движении ТТ не изменяется, а
при движении ТТ не изменяется, а  , в случае вращения тела вокруг неизменной оси (например, оси z)
, в случае вращения тела вокруг неизменной оси (например, оси z)  , где
, где  – проекция на ось z момента внешних сил, действующих на ТТ.
– проекция на ось z момента внешних сил, действующих на ТТ.
Уравнения  и
и  можно считать уравнениями движения. Первое из них имеет вид уравнения Ньютона для точки. Решение второго уравнения
можно считать уравнениями движения. Первое из них имеет вид уравнения Ньютона для точки. Решение второго уравнения 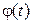 совместно с функцией
совместно с функцией  является законом движения твердого тела.
является законом движения твердого тела.
Пусть внешние силы отсутствуют, так что  и
и  . Тогда
. Тогда  , т. е.
, т. е.  . Центр масс ТТ движется прямолинейно и равномерно. Кроме того,
. Центр масс ТТ движется прямолинейно и равномерно. Кроме того, 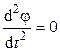 , т. е.
, т. е.  . Таким образом, в отсутствие внешних сил твердое тело вращается, причем скорость его вращения постоянна.
. Таким образом, в отсутствие внешних сил твердое тело вращается, причем скорость его вращения постоянна.
Твердое тело в большинстве случаев можно рассматривать как вещество, сплошь заполняющее некоторый объем пространства. Тогда выражение для момента инерции относительно некоторой оси удобно находить, разбивая ТТ на маленькие участки объема, которые можно принять за точки, каждая из которых имеет массу  где
где  – объем участка;
– объем участка;  – плотность, которая, вообще говоря, является функцией координат. Теперь момент инерции ТТ относительно некоторой оси можно представить в виде интеграла по объему всего тела:
– плотность, которая, вообще говоря, является функцией координат. Теперь момент инерции ТТ относительно некоторой оси можно представить в виде интеграла по объему всего тела: 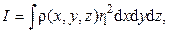 где
где  – расстояние данной точки
– расстояние данной точки  от оси, вокруг которой происходит вращение ТТ. Если известны плотность массы тела в каждой точке и его геометрические размеры, данная задача решается путем интегрирования.
от оси, вокруг которой происходит вращение ТТ. Если известны плотность массы тела в каждой точке и его геометрические размеры, данная задача решается путем интегрирования.
Основные законы и формулы
Уравнение движения твердого тела в произвольной инерциальной системе отсчета имеют вид
|
|
|

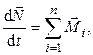
где  – масса тела;
– масса тела;  – скорость его центра масс;
– скорость его центра масс;  – момент импульса тела;
– момент импульса тела;  ,…,
,…,  – внешние силы, действующие на тело;
– внешние силы, действующие на тело;  ,…,
,…,  –моменты соответствующих сил.
–моменты соответствующих сил.
При вращении твердого тела с угловой скоростью  вокруг неподвижной оси
вокруг неподвижной оси  проекция момента импульса
проекция момента импульса 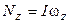 , где
, где 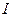 –момент инерции тела относительно этой оси. Тогда
–момент инерции тела относительно этой оси. Тогда

Момент силы относительно оси вращения
 ,
,
где  – радиус-вектор плеча силы (кратчайшее расстояние от оси вращения до линии действия силы
– радиус-вектор плеча силы (кратчайшее расстояние от оси вращения до линии действия силы  ).
).
В случае постоянного момента инерции
 ,
,
где  – угловое ускорение.
– угловое ускорение.
Момент инерции твердого тела относительно некоторой оси определяется выражением

где  ,
,  – плотность тела и элемент объема в окрестности некоторой точки;
– плотность тела и элемент объема в окрестности некоторой точки;  – расстояние от этой точки до оси;
– расстояние от этой точки до оси; 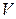 – область пространства, занимаемая телом.
– область пространства, занимаемая телом.
Момент импульса материальной точки
 или
или  ,
,
где  – расстояние от точки до оси, относительно которой определяется момент импульса;
– расстояние от точки до оси, относительно которой определяется момент импульса;  – масса точки;
– масса точки;  – линейная скорость.
– линейная скорость.
Момент инерции материальной точки
 .
.
Приведем момент инерции некоторых тел правильной геометрической формы. Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра
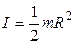 ,
,
где  – масса цилиндра;
– масса цилиндра;  – его радиус.
– его радиус.
Момент инерции полого цилиндра (обруча) относительно оси
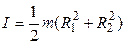 ,
,
где  и
и  – соответственно внутренний и внешний радиусы (у обруча
– соответственно внутренний и внешний радиусы (у обруча  ).
).
Момент инерции однородного шара радиусом  относительно оси, проходящей через его центр
относительно оси, проходящей через его центр
 .
.
Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно к его длине 
 .
.
Если система состоит из нескольких тел, ее момент инерции равен сумме моментов инерции этих тел.
Момент инерции 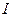 твердого тела относительно произвольной оси и момент инерции
твердого тела относительно произвольной оси и момент инерции  этого же тела относительно параллельной оси, проходящей через его центр инерции, связаны теоремой Штейнера:
этого же тела относительно параллельной оси, проходящей через его центр инерции, связаны теоремой Штейнера:
 ,
,
где  – масса тела;
– масса тела;  – расстояние между осями.
– расстояние между осями.
Кинетическая энергия вращения ТТ
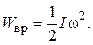
Контрольные вопросы
1. Чем определяется число степеней свободы твердого тела?
2. Чему равно число степеней свободы твердого тела в различных случаях движения?
3. Как доказывается возможность представления скорости плоского движения твердого тела в виде суммы поступательной и вращательной скоростей?
|
|
|
4. Что такое мгновенная ось вращения?
5. Из каких скоростей слагается скорость точек твердого тела при произвольном движении?
6. Если тело движется поступательно, то где находится мгновенная ось вращения?
7. Как связана возможность устойчивого вращения твердого тела с расположением по отношению к этому телу главных осей инерции?
8. Почему для плоского движения уравнение движения и уравнение моментов целесообразно записывать относительно точки, через которую проходит центральная главная ось, перпендикулярная плоскости движения?
9. Чему равно ускорение центра масс тела, имеющего массу m и находящегося под действием сил  и
и 
10. От каких величин зависит угловое ускорение тела?
11. Могут ли момент импульса и угловая скорость вращающегося тела быть неколлинеарными?
12. Относительно какой оси момент инерции однородного шара минимален и почему?
13. Почему знание массы тела является недостаточным для описания его инерционных свойств?
14. Дайте определение момента инерции.
15. Докажите теорему Гюйгенса–Штейнера.
16. Рассчитайте момент инерции однородного шара относительно оси, проходящей через его центр.
17. Рассчитайте момент инерции прямоугольного параллелепипеда относительно осей, проходящих через центр масс тела перпендикулярно его граням.
18. Проведите расчет момента инерции маятника Максвелла.
19. В каком случае кинетическая энергия вращающегося тела определяется формулой 
20. Почему, когда вращающийся на льду на коньках фигурист хочет остановиться, то разводит в стороны руки?
21. Как, располагая определенным количеством металла, создать маховик, который обладал бы максимальным моментом инерции?
22. Как поведет себя кабина вертолета, находящегося в полете, если по каким-либо причинам хвостовой винт перестанет работать?
23. Почему очень трудно удержаться на стоящем двухколесном велосипеде и совсем нетрудно сделать это, когда велосипед движется?
24. Что такое оси свободного вращения? Какие из них устойчивы?
25. В чем состоит нутация? От чего зависит скорость нутации? Почему однородный шар не может иметь нутационного движения?
|
|
|
26. Что такое прецессия гироскопа? Чем прецессия отличается от нутации?
27. При каких условиях можно считать, что вектор момента импульса гироскопа, мгновенная угловая скорость вращения и ось симметрии совпадают?
28. От чего зависит скорость прецессии?
29. Какие применения гироскопов известны?
30. Объяснить возникновение гироскопических сил. Какова их природа?
31. Чем уравновешивается момент внешних сил при прецессии гироскопа?
32. Что происходит с угловой скоростью прецессии гироскопа при уменьшении скорости вращения гироскопа вокруг его оси?
Примеры решения задач
Задача 1
Три шара с массами 2,5 кг, 4,0 кг и 2,0 кг укреплены в указанном порядке на невесомом стержне. Расстояние от левого конца стержня до первого шара равно 0,1 м, между центрами первого и второго шаров 0,2 м, а между центрами второго и третьего шаров 0,25 м. На каком расстоянии от левого конца стержня находится центр масс этой системы?
Решение.
 Рис. 4.1
Рис. 4.1
|
Поскольку шары относительно оси стержня расположены симметрично, то достаточно ввести одну ось OX, совпадающую со стержнем, как показано на рис. 4.1.
Координата центра масс системы шаров определяется выражением
 .
.
Для рассматриваемого случая получаем
 .
.
Подставляем исходные данные из условия задания
 м.
м.
Ответ:  м.
м.
Задача 2
Платформа в виде диска радиусом  м и массой
м и массой  кг вращается по инерции вокруг вертикальной оси, делая
кг вращается по инерции вокруг вертикальной оси, делая  с–1. В центре платформы стоит человек массой
с–1. В центре платформы стоит человек массой  кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
Решение.
Частота вращения платформы изменяется в результате действия, производимого человеком (его переходом на край платформы). В системе человек–платформа сила взаимодействия является внутренними, поэтому они не изменяют ни импульса, ни момента импульса системы. Поскольку все тела системы совершают вращательное движение вокруг неподвижной оси, то следует рассматривать только момент импульса системы.
Возникающие при переходе человека на край платформы внешние силы (силы реакции оси, силы тяжести и силы нормальной реакции) момента импульса системы не изменяют, поскольку моменты всех этих сил относительно вертикальной оси вращения равны нулю. Следовательно, момент импульса этой системы остается постоянным: 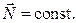 .
.
По закону сохранения момента импульса
 (4.3)
(4.3)
где  и
и  – моменты инерции платформы и стоящего в ее центре человека;
– моменты инерции платформы и стоящего в ее центре человека;  – угловая скорость платформы с человеком, стоящим в ее центре;
– угловая скорость платформы с человеком, стоящим в ее центре;  – момент инерции человека, стоящего на краю платформы;
– момент инерции человека, стоящего на краю платформы;  – угловая скорость платформы с человеком, стоящем на ее краю.
– угловая скорость платформы с человеком, стоящем на ее краю.
|
|
|
Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением
 (4.4)
(4.4)
Определив из уравнения (4.3)  и подставив полученное выражение
и подставив полученное выражение
в формулу (4.4), будем иметь
 (4.5)
(4.5)
Момент инерции платформы определяем как для диска. Следовательно,

Момент инерции человека рассчитываем как для материальной точки. Поэтому 
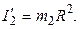
Угловая скорость платформы до перехода человека из ее центра на край платформы 
Заменив в формуле (4.5) величины  ,
,  ,
,  ,
,  их выражениями, получаем:
их выражениями, получаем:
 0,94 м/с.
0,94 м/с.
Ответ:  0,94 м/с.
0,94 м/с.
Задача 3
Определить закон движения центра масс диска, имеющего радиус  массу
массу  . К оси диска приложена постоянная сила
. К оси диска приложена постоянная сила  и момент
и момент 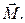 Коэффициент трения качения
Коэффициент трения качения 
Решение.

Рис. 4.2
Второй закон Ньютона в проекциях на оси  и
и  записывается в виде (рис. 4.2)
записывается в виде (рис. 4.2)
 ,
,  ,
,
где  – движущая сила;
– движущая сила;  – нормальная сила реакции опоры поверхности;
– нормальная сила реакции опоры поверхности;  – сила трения. Основной закон динамики для вращательного движения в этом случае имеет вид
– сила трения. Основной закон динамики для вращательного движения в этом случае имеет вид

где  .
.
Так как  то
то  и
и  . Поскольку
. Поскольку
 , то
, то
 .
.
Здесь учтено условие качения диска без скольжения  , откуда
, откуда  (мгновенная ось вращения диска находится в точке Р). Подставив полученное выражение для силы трения, получим выражение для ускорения:
(мгновенная ось вращения диска находится в точке Р). Подставив полученное выражение для силы трения, получим выражение для ускорения:
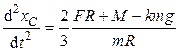 .
.
Проинтегрировав последнее равенство дважды, получим

Если в начальный момент диск находился в покое, то  если начало координат совпадает с начальным положением мгновенной оси вращения, то
если начало координат совпадает с начальным положением мгновенной оси вращения, то  . Из выражения для
. Из выражения для 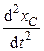 следует, что движение диска в заданном направлении возможно при условии
следует, что движение диска в заданном направлении возможно при условии  или
или  . Однако качение без скольжения может быть при значениях
. Однако качение без скольжения может быть при значениях  не превосходящих предельного значения силы трения
не превосходящих предельного значения силы трения  т. е.
т. е. 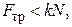 или с учетом
или с учетом  имеем
имеем  откуда
откуда  Следовательно,
Следовательно,
 .
.
Ответ:  , при условии
, при условии  .
.
Задача 4
Полый цилиндр с внутренним радиусом  и внешним
и внешним 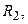 массой
массой  и длиной
и длиной 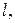 вращается вокруг оси
вращается вокруг оси  проходящей через точку О и перпендикулярной геометрической оси цилиндра. При этом ось симметрии цилиндра лежит на радиусе окружности вращения. Найти момент инерции цилиндра относительно оси
проходящей через точку О и перпендикулярной геометрической оси цилиндра. При этом ось симметрии цилиндра лежит на радиусе окружности вращения. Найти момент инерции цилиндра относительно оси  если центр масс цилиндра находится от нее на расстоянии a.
если центр масс цилиндра находится от нее на расстоянии a.
Решение.
Для того чтобы найти момент инерции тела относительно произвольной оси – в нашем случае, оси  необходимо воспользоваться теоремой Гюйгенса–Штейнера:
необходимо воспользоваться теоремой Гюйгенса–Штейнера:
 , (4.6)
, (4.6)
где  – момент инерции цилиндра относительно оси
– момент инерции цилиндра относительно оси  параллельной заданной оси
параллельной заданной оси  и проходящей через его центр масс (рис. 4.3).
и проходящей через его центр масс (рис. 4.3).

Рис. 4.3
Для решения разбиваем цилиндр на бесконечно тонкие диски массой  и толщиной
и толщиной  и определяем момент каждого диска относительно оси, лежащей в его плоскости и параллельной оси
и определяем момент каждого диска относительно оси, лежащей в его плоскости и параллельной оси  Момент инерции кольца относительно центра имеет вид
Момент инерции кольца относительно центра имеет вид
 .
.
Для плоского тела 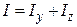 . Так как для однородного симметричного тела
. Так как для однородного симметричного тела  , то момент инерции диска относительно оси
, то момент инерции диска относительно оси  равен
равен
 . (4.7)
. (4.7)
Пусть один из дисков находится на расстоянии 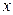 от оси
от оси  . Тогда по теореме Гюйгенса–Штейнера с учетом (4.7) момент инерции диска относительно оси
. Тогда по теореме Гюйгенса–Штейнера с учетом (4.7) момент инерции диска относительно оси  :
:
 . (4.8)
. (4.8)
Учитывая, что 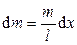 (4.9) и подставляя (4.9) в (4.8), получаем:
(4.9) и подставляя (4.9) в (4.8), получаем:
 (4.9)
(4.9)
Интегрируя по всей длине цилиндра, находим его момент инерции относительно оси z:
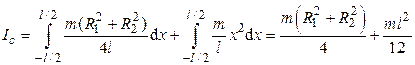 . (4.10)
. (4.10)
Из выражения (4.10) видно, что момент инерции цилиндра относительно оси, проходящей через его центр масс перпендикулярно геометрической оси, можно рассчитать как сумму соответствующих моментов инерции диска относительно диаметра и тонкого стержня относительно оси, проходящей через центр масс перпендикулярно стержню. Этим приемом можно воспользоваться при расчете моментов инерции сплошных и полых цилиндров относительно осей  , проходящих как через центр масс, так и через край цилиндра.
, проходящих как через центр масс, так и через край цилиндра.
И, наконец, подставляя (4.10) в (4.6), находим момент инерции цилиндра относительно оси 

Ответ: 
Задача 5
Найти момент инерции однородного тела массой  ограниченного параболоидом вращения и плоскостью
ограниченного параболоидом вращения и плоскостью  относительно его оси симметрии. Радиус основания параболоида равен
относительно его оси симметрии. Радиус основания параболоида равен  Указание: используйте уравнение параболоида
Указание: используйте уравнение параболоида  , где коэффициент
, где коэффициент  определяется при
определяется при 
Решение.
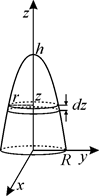 Рис. 4.4
Рис. 4.4
| Разобьем мысленно тело на бесконечно тонкие диски радиусом  и толщиной и толщиной  Тогда момент инерции каждого диска: Тогда момент инерции каждого диска:
 , где , где  – масса диска: – масса диска:  , ,  –плотность тела. Учитывая аддитивность момента инерции, получаем: –плотность тела. Учитывая аддитивность момента инерции, получаем:
 (4.11)
где (4.11)
где  – высота тела. – высота тела.
|
Чтобы вычислить интеграл (4.11), нужно найти уравнение параболоида. Из рис. 4.4 видно, что 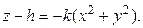 Коэффициент
Коэффициент  находим из условия, что при
находим из условия, что при  ,
,  тогда
тогда  Итак,
Итак,
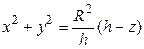 . (4.12)
. (4.12)
Подставляя выражение (4.12) в формулу (4.11), получаем
 (4.13)
(4.13)
Для исключения  и
и  из формулы (4.13) воспользуемся тем, что масса тела
из формулы (4.13) воспользуемся тем, что масса тела
 .
.
Отсюда 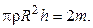 Подставляя это выражение в формулу (4.13), окончательно находим:
Подставляя это выражение в формулу (4.13), окончательно находим: 
Ответ: 
Задача 6
Материальная точка массой  движется по горизонтальной поверхности с постоянной скоростью
движется по горизонтальной поверхности с постоянной скоростью  В некоторый момент времени она ударяется в конец стержня массы
В некоторый момент времени она ударяется в конец стержня массы  длиной
длиной 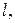 лежащей на поверхности перпендикулярно направлению скорости точки. Найти собственный момент импульса стержня после соударения.
лежащей на поверхности перпендикулярно направлению скорости точки. Найти собственный момент импульса стержня после соударения.
Решение.

Рис. 4.5
Материальная точка испытывает упругое соударение с концом стержня. После этого она продолжает движение вдоль прямой, на которой лежал ее вектор скорости, однако скорость будет изменена. В частном случае она окажется равной нулю. Стержень после соударения будет принимать участие в двух типах движения. С одной стороны, центр масс стержня будет перемещаться поступательно в том же направлении, что и материальная точка до соударения. С другой стороны, стержень будет вращаться вокруг центра масс (рис. 4.5). Собственный момент импульса стержня будет обусловлен его движением в системе отсчета, связанной с его центром масс
В системе будет выполняться закон сохранения импульса:
 , (4.14)
, (4.14)
где  – скорость материальной точки после соударения;
– скорость материальной точки после соударения;  – скорость центра масс стержня после соударения. Необходимо помнить, что закон сохранения записывается только для поступательных скоростей.
– скорость центра масс стержня после соударения. Необходимо помнить, что закон сохранения записывается только для поступательных скоростей.
Так же будет выполняться закон сохранения энергии:
 , (4.15)
, (4.15)
где  – момент инерции стержня относительно его центра масс;
– момент инерции стержня относительно его центра масс;  – угловая скорость вращения стержня относительно его центра масс.
– угловая скорость вращения стержня относительно его центра масс.
Закон сохранения момента импульса запишем в системе отсчета, связанной с центром масс стержня:
 . (4.16)
. (4.16)
Решая совместно систему уравнений (4.14)–(4.16) и учитывая, что собственный момент импульса стержня равен  , получим:
, получим:
из уравнения (4.16):
 (4.17)
(4.17)
из уравнения (4.14):
 (4.18)
(4.18)
Подставим полученные выражения (4.17) и (4.18) в (4.15):
 (4.19)
(4.19)
Из уравнения (4.19) выражаем 
 . (4.20)
. (4.20)
С учетом (4.20) находим собственный момент импульса стержня:
 .
.
Ответ: 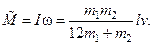
Задача 7
Однородный стержень круглого сечения радиусом 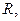 массой
массой  и длиной
и длиной  лежит на гладкой горизонтальной поверхности. Шарик радиусом
лежит на гладкой горизонтальной поверхности. Шарик радиусом  и массой
и массой  , двигаясь со скоростью
, двигаясь со скоростью  перпендикулярной к стержню, упруго ударяется об его конец на расстоянии
перпендикулярной к стержню, упруго ударяется об его конец на расстоянии  от торца. Считая, что
от торца. Считая, что  найти:
найти:
а) угловую скорость стержня, скорость его центра инерции и скорость шарика после удара;
б) зависимость доли переданной энергии от отношения масс  .
.
Решение.
Выбираем систему координат так, чтобы шарик и стержень лежали в плоскости XOY. Так как они имеют одинаковые радиусы, то после столкновения шарик не вылетит из плоскости XOY. Так как столкновение происходит на расстоянии  от торца, то шарик все время остается на первоначальной прямой, двигаясь после столкновения либо в прежнем направлении, либо в противоположном, или останавливается (в зависимости от
от торца, то шарик все время остается на первоначальной прямой, двигаясь после столкновения либо в прежнем направлении, либо в противоположном, или останавливается (в зависимости от  ). Поскольку трение отсутствует, а силы тяжести уравновешены силами реакции опоры, то выполняются законы сохранения импульса, энергии, момента импульса:
). Поскольку трение отсутствует, а силы тяжести уравновешены силами реакции опоры, то выполняются законы сохранения импульса, энергии, момента импульса:
 , (4.21)
, (4.21)
 , (4.22)
, (4.22)
 , (4.23)
, (4.23)
где  – скорость шарика после соударения;
– скорость шарика после соударения;  – скорость центра инерции стержня;
– скорость центра инерции стержня; 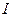 – момент инерции стержня относительно оси OZ. Так как по условию
– момент инерции стержня относительно оси OZ. Так как по условию  то можно взять
то можно взять
 (4.24)
(4.24)
Спроектируем уравнение (4.21) на ось OX, а уравнение (4.23) – на ось OZ:
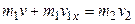 ,
,
 . (4.25)
. (4.25)
Так как  то
то  Кроме того,
Кроме того, 
Следовательно, уравнение (4.25) можно переписать в виде

С учетом формулы (4.24) и того, что  вместо уравнения (4.21)–(4.23) имеем:
вместо уравнения (4.21)–(4.23) имеем:
 , (4.26)
, (4.26)
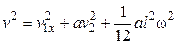 , (4.27)
, (4.27)
 ,
, 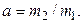 (4.28)
(4.28)
Из уравнения (4.26) и (4.28) получаем  откуда
откуда
 (4.29).
(4.29).
Подставляя выражение для  в уравнение (4.27), приходим к системе из двух уравнений с двумя неизвестными:
в уравнение (4.27), приходим к системе из двух уравнений с двумя неизвестными:
 , (4.30)
, (4.30)
 (4.31)
(4.31)
Исключая из уравнения (4.31)  с помощью формулы (4.30), получаем
с помощью формулы (4.30), получаем
 .
.
Поскольку интересует ненулевое решение, то
 . (4.32)
. (4.32)
Из уравнений (4.28) и (4.29) находим:
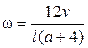 , (4.33)
, (4.33)
 (4.34)
(4.34)
Из выражения (4.34) следует, что при 
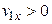 , при
, при  , при
, при 
 , т. е., если
, т. е., если  , шарик после столкновения будет двигаться в прежнем направлении; если
, шарик после столкновения будет двигаться в прежнем направлении; если  , шарик остановится; если же
, шарик остановится; если же 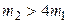 , шарик отскочит от стержня.
, шарик отскочит от стержня.
Энергия, передаваемая шариком стержню,
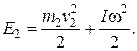 (4.35)
(4.35)
Подставляя в уравнение (4.35) выражения (4.24), (4.32), (4.33), получаем  . Учитывая, что начальная энергия
. Учитывая, что начальная энергия  , имеем
, имеем
 .
.
Используя стандартные методы исследования функции, находим, что максимальная передача энергии происходит при 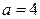 , т. е. при
, т. е. при  . В этом случае шарик передает всю свою энергию стержню и останавливается.
. В этом случае шарик передает всю свою энергию стержню и останавливается.
Задача 8
Стержень массой  и длиной
и длиной  , который может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через один из его
, который может свободно вращаться вокруг неподвижной горизонтальной оси, проходящей через один из его
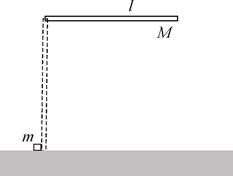 Рис. 4.6
Рис. 4.6
| концов, под действием силы тяжести переходит из горизонтального положения в вертикальное. Проходя через вертикальное положение, стержень нижним концом упруго ударяет малое тело массой  лежащее на столе. Найти, на какое расстояние лежащее на столе. Найти, на какое расстояние  переместится тело переместится тело  после удара, если коэффициент трения между телом и столом равен после удара, если коэффициент трения между телом и столом равен  и не зави- и не зави-
|
сит от скорости. Стержень после удара остановился. Тело скользит по столу без вращения.
Решение.
Применяя закон сохранения энергии к стержню до удара и закон сохранения момента импульса к системе стержень–тело во время удара, получим:
 , (4.36)
, (4.36)
 (4.37)
(4.37)
где  – угловая скорость вращения стержня в момент удара,
– угловая скорость вращения стержня в момент удара, 
|
|
|


