Алгоритм нахождения производной

Федеральное государственное образовательное бюджетное учреждение

Высшего образования

«ФИНАН

«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ

РОССИЙСКОЙ ФЕДЕРАЦИИ»

Департамент анализа данных, принятия решений и финансовых технологий

 

 

Р.М.Магомедов, Е.В.Маевский

 

Приближенное вычисление производной функции в заданной точке (Excel)

 

Учебно-методические рекомендации для проведения

семинара №5 по компьютерному практикуму

 

Для бакалавров направления 38.03.01 «Экономика»

 

Электронное издание

 

Москва 2017

Приближенное вычисление производной

Функции в заданной точке (Excel)

Введение

Пусть функция  определена в окрестности точки . Тогда производной функции  в точке  называется .

Простейшими формулами для приближенного численного вычисления производной являются так называемые двухточечные формулы, которые можно получить непосредственно из определения производной: , 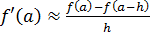. Такое название связано с тем, что указанные формулы позволяют оценить значение производной в точке по значениям функции в двух точках.

Если зафиксировать функцию и точку  и исследовать зависимость погрешности двухточечной оценки производной от малого шага , то можно доказать, что погрешность будет пропорциональна величине .

Более точная оценка получится, если использовать значения функции в трех точках: , , . Первая из этих формул используется при оценке производной на левой границе промежутка, вторая ­– во всех внутренних точках промежутка, а третья – на правой границе. Погрешности трехточечных формул пропорциональны .

Еще более точными являются формулы, оценивающие производную по большему количеству точек (4 и более). Однако следует иметь в виду, что увеличение количества участвующих в формуле точек усложняет вычисление по формуле и увеличивает ошибку округления, возникающую при этом вычислении. Потому, хотя и возможно теоретически использовать для оценки производной в данной точке весь массив известных значений функции, но на практике этого никогда не делают.

Другой способ уточнения значения производной – уменьшение шага . Такой подход представляется более рациональным для функций, заданных аналитическим выражением, но неприменим к функции, заданной таблицей значений.

Задание 1.  Вычислить в Excel приближенно производную функцию в заданной точке по следующему алгоритму.

Алгоритм нахождения производной

1. Составим таблицу значений функции  при , где , .

1.1. Вводим в диапазон ячеек A3:A23 рабочего листа Excel числа от -10 до 10 с шагом 1, как показано на рисунке. В ячейку C1 вводим число 1. В ячейку B3 вводим формулу для нахождения значений функции    при , где , .:

 =(A3^2+3*A3+1)/(A3^2+2*A3+2)

1.2. Копируем формулу до ячейки B23.

2. В каждой точке  при  оценим значение производной по двухточечной формуле . Изобразим соответствующую ломанную.

2.1. В ячейку C3 водим формулу:

=(((A3+$C$1)^2+3*(A3+$C$1)+1)/((A3+$C$1)^2+2*(A3+$C$1)+2)-((A3)^2+3*(A3)+1)/((A3)^2+2*(A3)+2))/$C$1

2.2. Копируем формулу до ячейки C23.

2.3. Для оформления и построения ломанной в ячейки A2, B2, C2 водим соответственно x, f(x), fᶦ(x) - в 2-х т., как показано на рисунке.

2.4. Выделяем диапазон ячеек A2:C23. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками., как показано на рисунке:

2.5. Нажимаем Ок.

2.6. В результате получиться ломанная как показано на рисунке выше.

3. В каждой точке  при  оценим значение производной по соответствующей трехточечной формуле. Изобразим ломанную.

3.1. В ячейку D3 водим формулу:

=(((A3+$C$1)^2+3*(A3+$C$1)+1)/((A3+$C$1)^2+2*(A3+$C$1)+2)-((A3-$C$1)^2+3*(A3-$C$1)+1)/((A3-$C$1)^2+2*(A3-$C$1)+2))/(2*$C$1)

3.2. Копируем формулу до ячейки D23.

3.3. Для оформления и построения ломанной в ячейку D2 водим fᶦ(x) - в 3-х т., как показано на рисунке.

3.4. Выделяем диаграмму.

3.5. Из контекстного меню выбираем команду Выбрать данные.

3.6. В окне Выбор источника данных задаем команду Добавить.

3.7. Заполняем окно Изменение ряда как показано на рисунке:

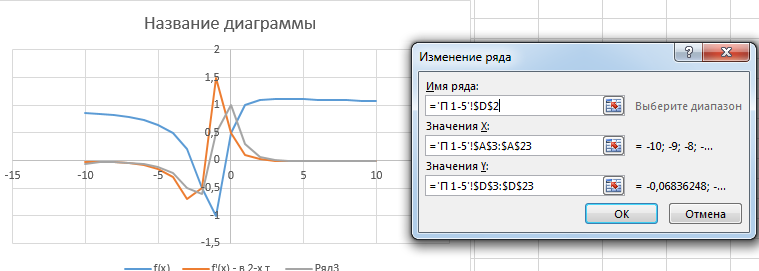
3.8. В результате получиться ломанная как показано на рисунке выше.

4. Составим таблицу точных значений производной  при тех же значениях .

4.1. В ячейку E3 водим формулу:

=(-(A3^2)+2*A3+4)/((A3^2+2*A3+2)^2)

4.2. Копируем формулу до ячейки E23.

4.3. Для оформления и построения ломанной в ячейку E2 водим fᶦ(x) точ, как показано на рисунке.

4.4. Как показано в пункте 3 в область диаграммы добавляем новые данные из диапазона E3:E23.

4.5. В результате должна получиться диаграмма как показано на рисунке:

5. Сравним точные значения производной с приближенными, построив три ломанные на одном графике.

5.1. Выделяем диапазон ячеек A2:A23, C2:E23, как показано на рисунке:

5.2. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:

6. Повторим вычисления пунктов 1-5, взяв величину шага .

6.1. Для этого на новом листе рабочей книги оформляем таблицу как показано на рисунке:

6.2. В ячейке B3 введена формула:

=A3*$D$1

6.3. В ячейке C3 введена формула:

=(((A3)^2+3*A3+1)/(A3^2+2*A3+2)-($D$1^2+3*$D$1+1)/($D$1^2+2*$D$1+2))/(A3-$D$1)

6.4. В ячейке D3 введена формула:

=(((B3+$D$1)^2+3*(B3+$D$1)+1)/((B3+$D$1)^2+2*(B3+$D$1)+2)-((B3)^2+3*(B3)+1)/((B3)^2+2*(B3)+2))/$D$1

6.5. В ячейке E3 введена формула:

=(((B3+$D$1)^2+3*(B3+$D$1)+1)/((B3+$D$1)^2+2*(B3+$D$1)+2)-((B3-$D$1)^2+3*(B3-$D$1)+1)/((B3-$D$1)^2+2*(B3-$D$1)+2))/(2*$D$1)

6.6. В ячейке F3 введена формула:

=(-(B3^2)+2*B3+4)/((B3^2+2*B3+2)^2)

6.7. Выделяем диапазон ячеек A2:A23, D2:F23/

6.8. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:

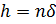7. Составим таблицу погрешностей двухточечной приближенной формулы, вычисляя разность  при , где , .

7.1. На новом листе рабочей книги Excel вводим в диапазон ячеек A4:A103 числа от -50, -49,…,-1,1,2,…,50 с шагом 1, как показано на рисунке (начало таблицы):

7.2. В ячейку C1 вводим число 0. В ячейку E1 вводим число 0,01.

7.3. В ячейку В4 вводим формулу:

 =A4*$E$1

7.4. В ячейку С4 вводим формулу:

=(-$C$1^2+2*$C$1+4)/(($C$1^2+2*$C$1+2)^2)-((B4^2+3*B4+1)/(B4^2+2*B4+2)-($C$1^2+3*$C$1+1)/($C$1^2+2*$C$1+2))/B4

8. Исследуем зависимость погрешности от , построив график по предыдущей таблице.

8.1. Выделяем диапазон ячеек A3:A103, C3:C103.

8.2. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке (см. пункт 9).

9. Повторим шаги 7-8 для погрешности трехточечной формулы .

9.1. В ячейку D4 вводим формулу:

=(-$C$1^2+2*$C$1+4)/(($C$1^2+2*$C$1+2)^2)-((B4^2+3*B4+1)/(B4^2+2*B4+2)-(-B4^2+3*(-B4)+1)/(-B4^2+2*(-B4)+2))/(2*B4)

9.2. Выделяем диапазон ячеек A3:A103, C3:D103.

9.3. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками. В результате должна получиться диаграмма как показано на рисунке:

Задание 2. Найти первую производную функции  в точке 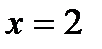. Заметим, что производная приведенной функции в точке , вычисленная аналитическим методом, равна 12 – это значение нам понадобится для проверки результата, полученного путем вычисления численным методом в электронной таблице.

Из вышесказанного известно, что выражение для вычисления производной функции одной переменной в точке x, имеет вид:

где  – очень малая конечная величина. То есть вместо выражения  можно взять достаточно маленькое число, например, 0,00001.

Примечание. Количество точек после запятой для выражения h зависить от того с какой заданной точностью нужно вычислить производную, если, например, производную нужно вычислить с точностью до 2 знаков после запятой, то достаточно взять h равной 0,0001.

Решение

Решим задачу двумя способами.

Способ 1

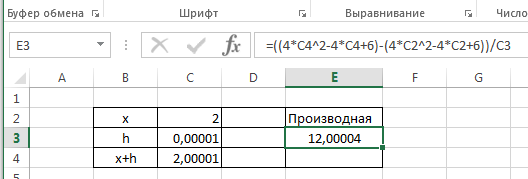
1. Вводим в ячейку C2 рабочего листа заданное значение аргумента, равное 2, в другой ячейке – C3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке C4 вычисляем сумму C3=C1+C2.

2. В ячейку E3 вводим формулу для вычисления производной:

 =((4*C4^2-4*C4+6)-(4*C2^2-4*C2+6))/C3.

3. После нажатия клавиши Enter получаем результат вычисления 12,00004 (см. рис.).

 

Способ 2

1. Зададим окрестность точки 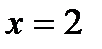 достаточно малого размера, например, значение слева  =1,99999, а значение справа 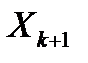=2,00001 и введем эти значения в ячейку B3 и B4 соответственно.

2. Вводим в ячейку рабочего листа формулу правой части заданной функциональной зависимости, например, в ячейку C3, как показано на рис., делая ссылку на ячейку B3, где находится значение х:

= 4*B3^2 -4*B3+6.

3. Копируем эту формулу в ячейку C4.

4. В ячейку E3 вводим формулу вычисления производной (рис.):

=(C4-C3)/(B4-B3).

В результате вычисления в ячейке E3 будет выведено приближенное значение производной заданной функции в точке 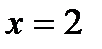, величина которой равна 12, что соответствует результату, полученному аналитически.

Задание 3. Найти первую производную функции  в точке .

Из вышесказанного известно, что выражение для вычисления первой производной функции одной переменной в точке x, имеет вид:

где  – очень малая конечная величина. То есть вместо выражения h можно взять достаточно маленькое число, например, 0,00001.

Решение

1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное =3*пи()/4, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В3 вычисляем сумму В3=В1+В2.

2. В ячейку E3 вводим формулу для вычисления производной:

 =((SIN(1+1/C4))^2-(SIN(1+1/C2))^2).

3. После нажатия клавиши Enter получаем результат вычисления 0,0000213 (см. рис.).

 

Задание 4. Найти вторую производную функции  в точке 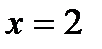. Заметим, что вторая производная приведенной функции в точке 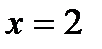, вычисленная аналитическим методом, равна 44 – это значение нам понадобится для проверки результата, полученного путем вычисления численным методом в электронной таблице.

Из математики известно, что выражение для вычисления второй производной функции одной переменной в точке 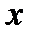, имеет вид:

где  – очень малая конечная величина. То есть вместо выражения  можно взять достаточно маленькое число, например, 0,00001.

Решение

1. Вводим в ячейку B2 рабочего листа заданное значение аргумента, равное 2, в другой ячейке – B3 укажем достаточно малое приращение аргумента – например 0,00001, в ячейке В4 вычисляем сумму В3=В1+В2.

2. В ячейку E3 вводим формулу для вычисления второй производной:

=(1/(C3^2))*(4*C4^3-2*C4^2-2*4*C2^3+2*2*C2^2+4*(C2-C3)^3-2*(C2-C3)^2).

3. После нажатия клавиши Enter получаем результат вычисления 44,00003917 (см. рис.).

Поделиться:

Воспользуйтесь поиском по сайту: