Задания для самостоятельной работы

Федеральное государственное образовательное бюджетное учреждение

Высшего образования

«ФИНАН

«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ

РОССИЙСКОЙ ФЕДЕРАЦИИ»

Департамент анализа данных, принятия решений и финансовых технологий

 

Р.М.Магомедов, Е.В. Маевский

 

Приближенное вычисление поведения функций вблизи точек разрыва. Графическое построение наклонных асимптот (Excel)

 

Учебно-методические рекомендации для проведения

семинара №4 по компьютерному практикуму

 

Для бакалавров направления 38.03.01 «Экономика»

 

Электронное издание

 

Москва 2017

Приближенное вычисление поведения функций вблизи точек разрыва. Графическое построение наклонных асимптот (Excel)

Введение

Пусть 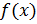 определена в окрестности точки 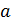, кроме быть может самой точки 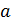. Наличие разрыва в точке  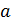означает, что .

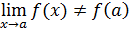1. Предположим, что 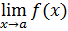 существует, но не равен значению 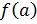, при этом последнее может существовать, а может не существовать, т.е. функция может быть не определена в точке 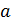. Такая ситуация называется устранимым разрывом. Типичный случай – неопределенность , которая раскрывается и в пределе получается число, например  .

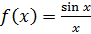2. Пусть 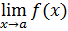 не существует, но существуют конечные односторонние пределы 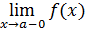, , 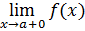не равные друг другу (поскольку не существует двусторонний предел). Эта ситуация называется (неустранимым) разрывом I-го рода. Типичные примеры функций с такими разрывами – неопределенности с модулями, например .

Иногда разрывом I-го рода называют разрыв, при котором существуют конечные односторонние пределы. Тогда рассмотренные два типа разрыва объединяются в один: разрыв будет устранимым, если односторонние пределы равны друг другу, и неустранимым – в противном случае.

3. Самым сложным типом разрыва является разрыв II-го рода, при котором хотя бы один из односторонних пределов бесконечен или не существует. Отметим сразу, что в случае отсутствия односторонних пределов, как например у функции , для численного исследования требуется дополнительная информация, уточняющая поведение функции в окрестности разрыва.

Рассмотрим более подробно ситуацию, когда оба односторонних пределов бесконечны. В этом случае вертикальная прямая 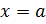 называется (двусторонней) вертикальной асимптотой графика функции 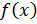. Типичным примером здесь является  при 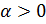. Показатель степени  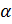можно вычислить через предел 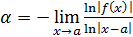. Зная 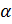, найдем коэффициент .

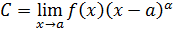Пусть теперь функция 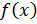 определена при всех достаточно больших значениях 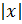. График функции имеет наклонную асимптоту  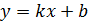на , если существуют числа  при которых 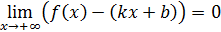. Аналогично определяется наклонная асимптота на 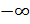. В частном случае, когда 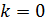, т.е. когда наклонная асимптота является горизонтальной прямой, говорят о горизонтальной асимптоте. Наличие асимптот на  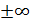означает, что график функции вдалеке от начала координат практически сливается с некоторой прямой.

Коэффициенты наклонных асимптот вычисляются по формулам:

, .

 

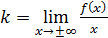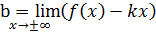Выполнение работы

1. Для функции 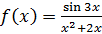 вычислим таблицу значений при , где 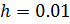, 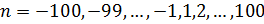. Построим две линии по найденным точкам: отдельно для отрицательных и положительных 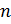. Найдем численно значение предела .

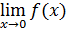1.1. Вводим в диапазон ячеекA4:A203 рабочего листа Excel числа 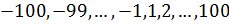. В ячейку C1 вводим число 0,01.

1.2. В ячейку В4 вводим формулу =A4*$C$1. Копируем формулу до ячейки В203.

1.2.1 В ячейку С4 вводим формулу =SIN(3*B4)/(B4^2+2*B4). Копируем формулу до ячейки С203.

1.3. Выделяем диапазон ячеек В4:С103. Задаем команду ВСТАВКА/ДИАГРАММЫ и выбираем тип диаграммы Точечная с прямыми отрезками., как показано на рисунке:

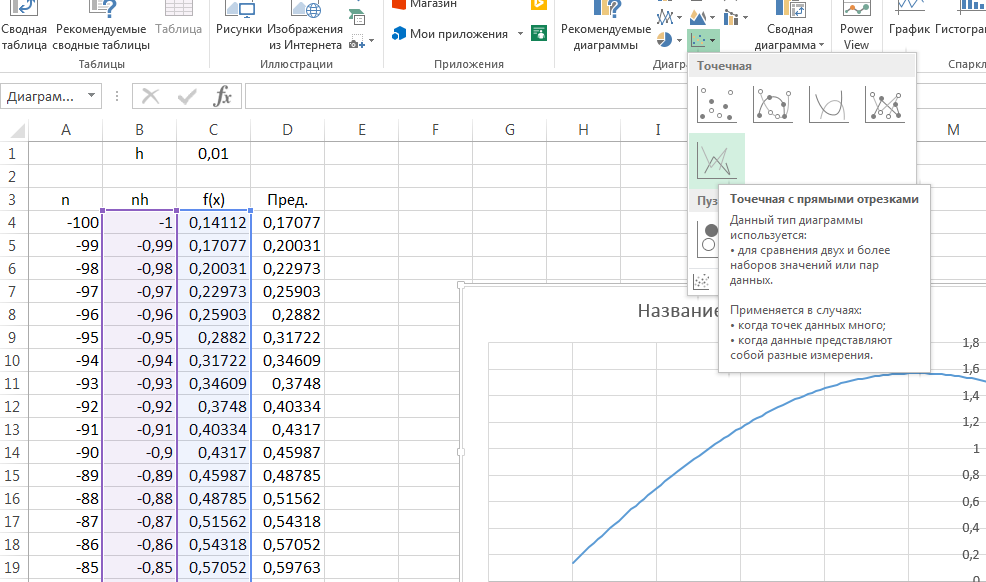
1.4. Оформляем таблицу как показано на рисунке выше.

1.5.Выделяем диаграмму.

1.6. Из контекстного меню выбираем команду Выбрать данные.

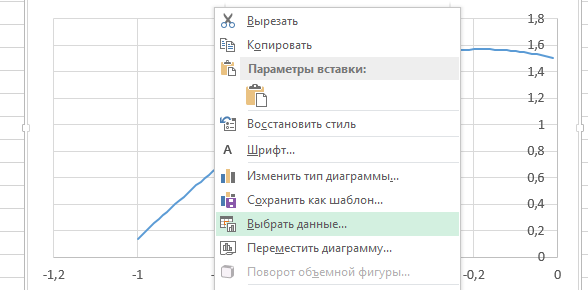
1.7. В окне Выбор источника данных задаем команду Добавить.

1.8.Заполняем окно Изменение ряда как показано на рисунке:

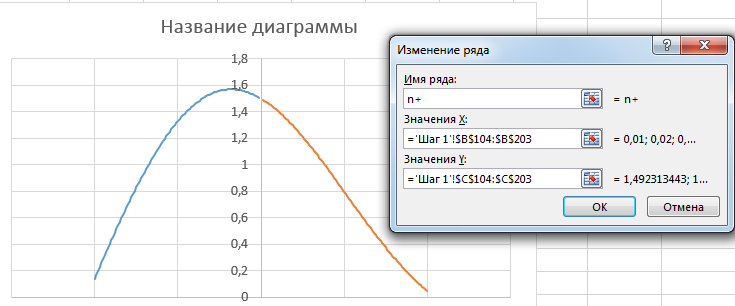
1.9. В результате получится ломанная как показано на рисунке выше.

1.10. В ячейку D4 введем формулу для вычисления численно значение предела :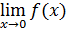

=SIN(3*(B4+$C$1))/((B4+$C$1)^2+2*(B4+$C$1))

1.11. Копируем эту формулу до ячейки D203/

1.12. Задаем имя листа Шаг 1.

2. Повторим то же построение для 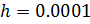. Уточним значение предела.

2.1. Создаем копию листа Шаг 1. Для этого из контекстного меню листа Шаг 1 (см. рис.) выбираем команду Переместить или скопировать….

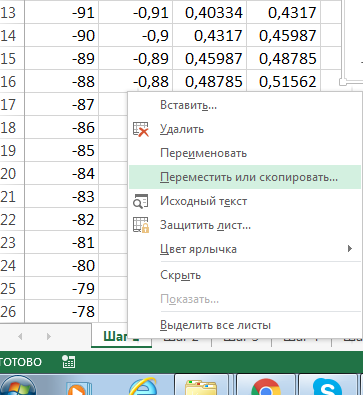
2.2. Оформляем окно Переместить или скопировать как показано на рисунке:

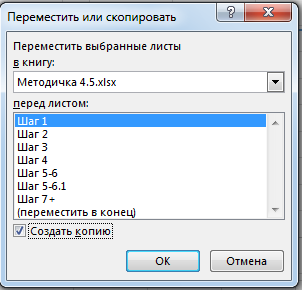
2.3. Задаем имя Шаг 2 для получившегося листа.

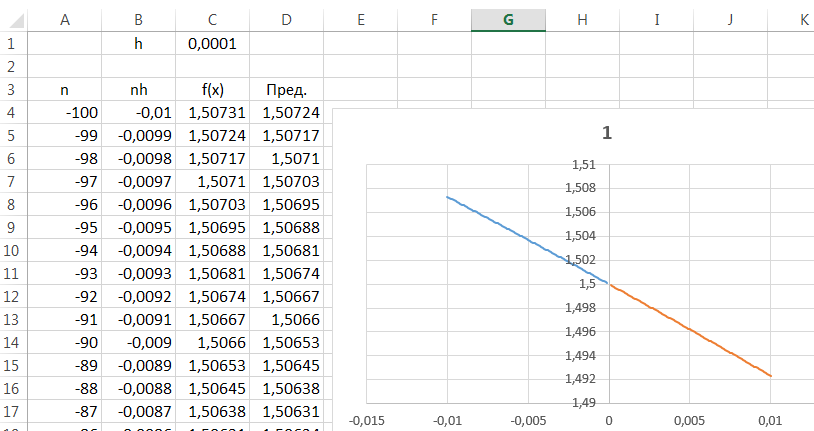
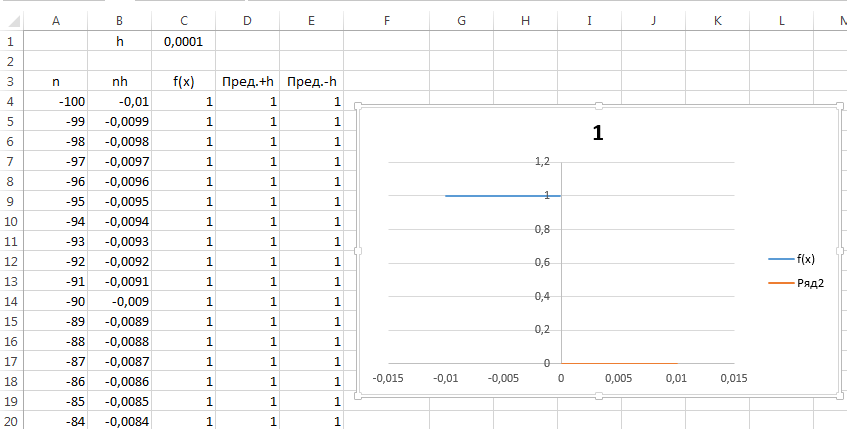
2.4. На Листе Шаг 2, меняем значение ячейки С1 на 0,0001.

2.5. В результате у вас должно получиться данные как показано на рисунке.

3. Для функции 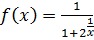 вычислим таблицу значений при , где 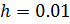, 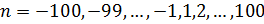. Построим две линии по найденным точкам: отдельно для отрицательных и положительных 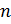.Найдем численно значения односторонних пределов , .

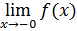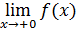3.1. Создаем новый лист и задаем имя Шаг 3.

3.2. Вводим в диапазон ячеекA4:A203 рабочего листаExcelчисла 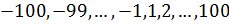. В ячейку C1 вводим число 0,01.

3.3. В ячейку В4 вводим формулу =A4*$C$1. Копируем формулу до ячейки В203.

3.3.1. В ячейку С4 вводим формулу =1/(1+2^(1/B4)). Копируем формулу до ячейки В203.

3.4. Строим две линии по найденным точкам: отдельно для отрицательных и отдельно для положительных 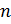, как показано в пп. 1.3-1.8.

3.5. В результате должно получиться две линии как показано на рисунке:

3.6. Оформляем таблицу как показано на рисунке.

3.7. В ячейку D4 введем формулу для вычисления численно значение предела :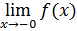

=1/(1+2^(1/(B4+$C$1)))

3.8. В ячейку E4 введем формулу для вычисления численно значение предела :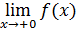

=1/(1+2^(1/(B4-$C$1))).

4. Повторим то же построение для 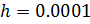. Уточним значения пределов.

4.1 Создаем копию листа Шаг 3, как показано в пп. 2.1.-2.4. Задаем имя листа Шаг 4.

4.2. На Листе Шаг 4, меняем значение ячейки С1 на 0,0001.

4.3. В результате у вас должно получиться данные как показано на рисунке.

5. Для функции 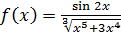 вычислим таблицу значений при , где 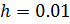, 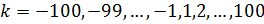. Построим две линии по найденным точкам: отдельно для отрицательных и положительных .

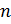5.1. Создаем новый лист и задаем имя Шаг 5-6.

5.2. Вводим в диапазон ячеекA4:A203 рабочего листаExcelчисла 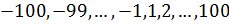. В ячейку C1 вводим число 0,01.

5.3.В ячейку В4 вводим формулу =A4*$C$1. Копируем формулу до ячейки В203.

5.3.1. В ячейку С4 вводим формулу =SIN(2*B4)/(B4^5+3*B4^4)^(1/3). Копируем формулу до ячейки В203.

5.4. Строим две линии по найденным точкам: отдельно для отрицательных и отдельно для положительных 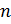, как показано в пп. 1.3-1.8.

5.5. В результате у Вас получаться две ломанные как показано на рисунке.

6. Для исследуемой функции вычислимзначения 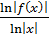 в тех же точках  и, построив соответствующие две линии, оценим значение .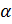

6.1. На листе Шаг 5-6, в ячейке D5 водим формулу для вычисления значения :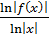

=-LN(ABS(C5))/LN(ABS(B5))

6.2. Копируем формулу до ячейки D202.

6.3. Выделив соответствующие диапазоны ячеек (для отрицательных nB4:B103, D4:D103; положительных nB104:B203, D104:D202) cтроим две линии по найденным точкам: отдельно для отрицательных и отдельно для положительных 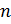, как показано в пп. 1.3-1.8.В результате должно получиться две линии как показано на рисунке.

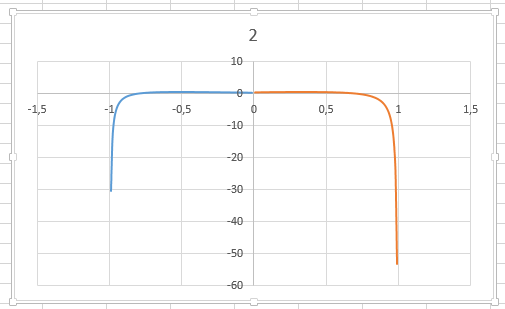
6.4. Значение 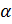 берем из ячейки D103 равное -0,404555323102164.

7. Для исследуемой функции и найденного 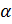 вычислим значения  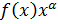в тех же точках  и, построив соответствующие две линии, оценим значение .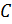

7.1. На листе Шаг 5-6 для вычисления значения 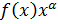 введем в ячейку E5 формулу:

=C5*ABS(B5)^$D$103

7.2. Выделив соответствующие диапазоны ячеек (для отрицательных nB4:B103, E4:E103; положительных nB104:B203, E104:E202) cтроим две линии по найденным точкам: отдельно для отрицательных и отдельно для положительных 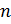, как показано в пп. 1.3-1.8.В результате должно получиться две линии как показано на рисунке.

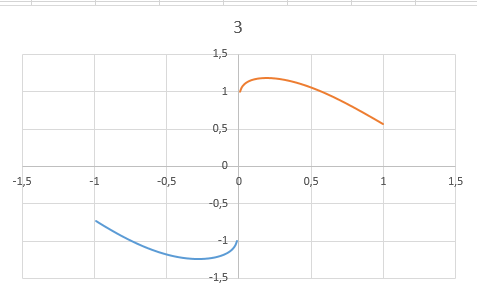
7.3.Значение C берем из ячейки E102 равное -1,02492234237999.

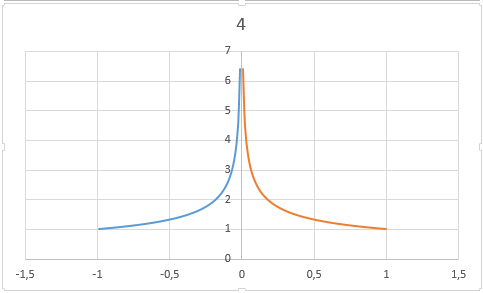
8. По тому же массиву точек  построим две ветви графика 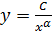 и сравним его с графиком исходной функции.

8.1. На листе Шаг5-6, в ячейке F5 для вычисления значения 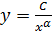 вводим формулу:

=$E$104/(ABS(B5)^$D$104)

8.2. Выделив соответствующие диапазоны ячеек (для отрицательных n B4:B103, F4:F103; положительных n B104:B203, F104:F202) cтроим две линии по найденным точкам: отдельно для отрицательных и отдельно для положительных 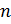, как показано в пп. 1.3-1.8. В результате должно получиться две линии как показано на рисунке.

9. Повторим построения пунктов 5-8 для 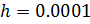, уточняя значения всех пределов.

9.1. Создаем копию листа Шаг 5-6, как показано в пп. 2.1.-2.4. Задаем имя листа Шаг 7.

4.2. На Листе Шаг 7, меняем значение ячейки С1 на 0,0001.

10. Для функции 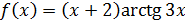 вычислим таблицу значений при , где 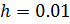, 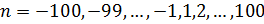. Построим две линии по найденным точкам: отдельно для отрицательных и положительных .

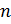10.1. Создаем новый лист и задаем имя Шаг 8.

10.2. Вводим в диапазон ячеекA4:A203 рабочего листаExcelчисла 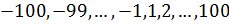. В ячейку C1 вводим число 0.01.

10.3.В ячейку В4 вводим формулу =A4*$C$1. Копируем формулу до ячейки В203.

10.4. В ячейке С5 водим формулу для вычисления значения :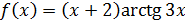

=(B4+2)*ATAN(3*B4)

10.5. Строим две линии по найденным точкам: отдельно для отрицательных и положительных .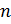

11. Для исследуемой функции вычислим значения  в тех же точках  и, построив соответствующие две линии, оценим значения .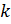

11.1. На листе Шаг 8, в ячейке D4 вводим формулу для вычисления значения

=C4/B4

11.2. Строим две линии по найденным точкам: отдельно для отрицательных и положительных .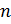

11.3. Значение 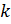 беремдля отрицательной бесконечностиравное 1,24904577239825 (из ячейки D4), для положительной
бесконечности из ячейки D203 равное3,74713731719476.

12. Для исследуемой функции и найденных 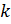 вычислим значения  в тех же точках  и, построив соответствующие две линии, оценим значения .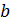

12.1. На листе Шаг 8, в ячейке E4 вводим формулу для вычисления значения  для отрицательной бесконечности:

=C4-$D$4*B4. Копируем формулу до ячейки E103.

12.2. в ячейке E104вводим формулу для вычисления значения  для положительной бесконечности:

=C4-$D$203*B4. Копируем формулу до ячейки E203.

12.3. Строим две линии по найденным точкам: отдельно для отрицательных и положительных .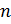

12.4. Значение 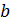 берем для отрицательной бесконечностиравное 1,27119062808401 (из ячейки D5), для положительной
бесконечности из ячейки D202 равное 3,76322770096158.

13. По тому же массиву точек  построим две наклонные асимптоты 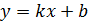 и сравним их с графиком исходной функции.

13.1. На листе Шаг 8, в ячейке F4 вводим формулу для вычисления значения 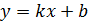 для отрицательной бесконечности:

=$D$4*B4+$D$5. Копируем формулу до ячейки F103.

13.2. В ячейке F104 вводим формулу для вычисления значения 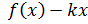 для положительной бесконечности:

=$D$4*B4+$D$202. Копируем формулу до ячейки F203.

13.3. Строим две линии по найденным точкам: отдельно для отрицательных и положительных .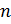

14. Повторим построения пунктов 10-13 для 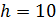, уточняя значения всех пределов.

14.1. Создаем копию листа Шаг8, как показано в пп. 2.1.-2.4. Задаем имя листа Шаг 9.

14.2. На Листе Шаг 9, меняем значение ячейки С1 на 0.001.

 

Задания для самостоятельной работы

1. Исследуйте с помощью Excel точки разрыва следующих функций: , ,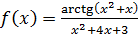

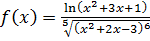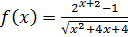
2. Исследуйте с помощью Excel наклонные асимптоты следующих функций: ,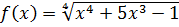

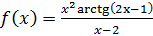
Поделиться:

Воспользуйтесь поиском по сайту: