для промежуточной аттестации в 10 классе.

Экзаменационные билеты по геометрии

 

Билет №1.

 

1. Сформулируйте аксиомы стереометрии и их следствия. Сделайте чертежи и пояснения.
2. Дайте определение параллельных плоскостей. Сформулируйте свойства параллельных плоскостей. Сделайте пояснения и чертежи.
3. Верно ли утверждение: если две прямые в пространстве перпендикулярны к третьей прямой, то эти прямые параллельны? Поясните.
4. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани
   10 см. Найдите площадь боковой и полной поверхности призмы.

 

Билет №2.

 

1. Сформулируйте определение параллельных прямой и плоскости. Сформулируйте признак параллельности прямой и плоскости. Сделайте чертежи и пояснения.
2. Тетраэдр и его элементы. Правильный тетраэдр и его свойства. Сделайте чертежи и пояснения.
3. Сколько двугранных углов имеет прямоугольный параллелепипед? Сделайте чертеж и укажите несколько.
4. В правильной треугольной пирамиде апофема образует с плоскостью основания угол 30º. Сторона основания равна 12 см. Найдите площадь поверхности пирамиды.

 

 

Билет №3.

 

1. Сформулируйте определение скрещивающихся прямых. Сформулируйте признак скрещивающихся прямых. Сделайте чертежи и пояснения.

2. Сформулируйте теоремы о трех перпендикулярах: прямую и обратную. Сделайте пояснения и чертежи. Приведите примеры.

3. Одна из двух прямых перпендикулярна к плоскости, а другая – не перпендикулярна к ней. Могут ли эти прямые быть параллельными? Поясните.

4. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы

Билет №4.

 

1. Опишите взаимное расположение прямых в пространстве. Как определяется угол между двумя прямыми в пространстве? Сделайте пояснения и чертежи.

2. Прямоугольный параллелепипед и его свойства.

3. Прямые а и b пересекаются. Прямая с является скрещивающейся с прямой а. Могут ли прямые b и с быть параллельными? Ответ обоснуйте.

4. В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 60º. Высота пирамиды равна 6 см. Найдите площадь боковой поверхности пирамиды.

 

 

Билет №5.

1. Перпендикулярность прямой и плоскости. Сформулируйте признак перпендикулярности прямой и плоскости. Сделайте чертежи и пояснения.

2. Понятие многогранника. Призма и ее элементы. Наклонная и правильная призмы.

3. Могут ли две плоскости, перпендикулярные к третьей плоскости, быть по отношению друг к другу перпендикулярными? Поясните.

4. Высота правильной четырехугольной пирамиды равна 6 см и образует с боковой гранью угол 30º. Найдите площадь боковой поверхности пирамиды.

 

 

Билет №6.

1. Сформулируйте лемму о параллельных прямых, перпендикулярных третьей. Сделайте чертежи и пояснения.

2. Расстояние от точки до плоскости. Сделайте пояснения и чертежи.

3. Прямая МА проходит через вершину квадрата ABCD и не лежит в плоскости квадрата.
а) Докажите, что МА и ВС – скрещивающиеся прямые.
б) Найдите угол между прямыми МА и ВС, если .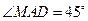

4. Через вершину прямого угла К треугольника DKF проведена прямая КМ, перпендикулярная к плоскости этого треугольника. Известно, что КМ = 15 см,
FK = DK = 10 см. Найдите расстояние от точки М до прямой DF.

Билет №7.

 

1. Сформулируйте лемму о параллельных прямых, пересекающих плоскость. Сделайте пояснения и чертежи.

2. Двугранный угол. Линейный угол двугранного угла.

3. Верно ли утверждение: если одна прямая параллельна плоскости, а другая прямая перпендикулярна этой плоскости, то прямые перпендикулярны друг другу?

4. В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 60º. Сторона основания пирамиды равна 8 см. Найдите площадь боковой поверхности пирамиды.

 

Билет №8.

 

1. Сформулируйте определение параллельных плоскостей. Сформулируйте признак параллельности двух плоскостей.

2. Опишите правила сложения и вычитания векторов, суммы нескольких векторов. Поясните на примерах с использованием чертежа прямоугольного параллелепипеда.

3. Плоскость α проходит через середины боковых сторон АВ и CD трапеции ABCD – точки M и N.
а) Докажите, что .
б) Найдите ВС, если AD=10см, NM=8см.

4. Дан куб ABCDA₁B₁C₁D₁. Точки К, М и Т – середины ребер СС₁, В₁С₁ и С₁D₁ соответственно. Найдите АС₁, если периметр сечения куба плоскостью КМТ равен см.

 

 

Билет №9.

 

1. Угол между прямой и плоскостью.

2. Правильная пирамида. Перечислите свойства правильной пирамиды.

3. Прямая CD проходит через вершину треугольника ABC и не лежит в плоскости ABC. E и F – середины отрезков АВ и ВС.
а) Докажите, что CD и EF – скрещивающиеся прямые.
б) Найдите угол между прямыми CD и EF, если .

4. В правильной треугольной пирамиде сторона основания равна высоте и равна 12 см. Найдите площадь поверхности пирамиды.

Билет №10.

 

1. Параллелепипед и его элементы. Сделайте чертеж и пояснения.

2. Векторы в пространстве. Равенство векторов. Классификация векторов. Приведите примеры, используя чертеж прямоугольного параллелепипеда.

3. Точка М не лежит в плоскости трапеции ABCD (AB║CD).
а) Докажите, что треугольники MAD и MBC имеют параллельные средние линии.
б) Найдите длины этих средних линий, если AD:BC=5:3, а средняя линия трапеции равна 16см.

4. Дан куб ABCDA₁B₁C₁D₁. Диагональ АС₁ равна .Найдите периметр сечения куба плоскостью РТН, где точки Р, Т и Н – середины ребер ВС, ВВ₁ и АВ соответственно.

 

Билет №11.

 

1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.

2. Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. Поясните правила на чертеже прямоугольного параллелепипеда.

3. Верно ли утверждение, что все прямые, перпендикулярные к данной плоскости и пересекающие данную прямую, лежат в одной плоскости? Поясните.

4. Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь полной и боковой поверхности призмы.

Билет №12.

 

1. Признак перпендикулярности прямой и плоскости.

2. Понятие многогранника. Пирамида и ее элементы. Усеченная и правильная пирамиды.

3. Через вершину А квадрата ABCD проведена прямая КА, не лежащая в плоскости квадрата.
а) Докажите, что КА и CD – скрещивающиеся прямые.
б) Найдите угол между КА и CD, если , .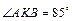

4. Через вершину угла Е прямоугольного треугольника НРЕ с гипотенузой НЕ проведена прямая МЕ, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки М до плоскости ЕРН, если ЕР = 5 см, а расстояние от точки М до прямой РН равно 10.

 

 

Билет №13.

1. Угол между прямой и плоскостью. Приведите примеры величины угла между прямой и плоскостью. Сделайте чертежи и пояснения.

2. Компланарные векторы. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам. Сделайте пояснения на примере прямоугольного параллелепипеда.

3. Треугольник АВС и трапеция KMNP имеют общую среднюю линию EF, причем KP║MN, EF║AC.
а) Докажите, что AC║KP.
б) Найдите KP и MN, если KP:MN=3:5, а AC=16см.

4. Через вершину прямого угла С равнобедренного треугольника DСЕ проведена прямая СК, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки К до прямой DЕ, если СК = 35 см, CD = см.

 

Билет №14.

 

1. Признак перпендикулярности двух плоскостей.

2. Понятие призмы, ее элементы, правильная призма. Перечислите свойства правильной четырехугольной призмы.

3. Диагональ квадрата перпендикулярна к некоторой плоскости. Каково расположение другой его диагонали по отношению к этой плоскости? Поясните.

4. Основание прямой призмы – прямоугольный треугольник с гипотенузой 25 см и катетом 20 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.

 

Билет №15.

1. Сформулируйте определение параллельных плоскостей. Сформулируйте признак параллельности двух плоскостей.

2. Понятие призмы, ее элементы, правильная призма. Перечислите свойства правильной четырехугольной призмы.

3. Верно ли утверждение: если одна прямая параллельна плоскости, а другая прямая перпендикулярна этой плоскости, то прямые перпендикулярны друг другу? Поясните на чертеже.

4. Высота правильной четырехугольной пирамиды равна 16 см, а боковое ребро пирамиды равно 20 см. Найдите площадь боковой поверхности пирамиды.

 

Билет №16.

1. Сформулируйте аксиомы стереометрии и их следствия. Сделайте чертежи и пояснения.

2. Правильная пирамида. Перечислите свойства правильной треугольной пирамиды.

3. Можно ли через одну и ту же точку пространства провести три плоскости, каждые две из которых будут друг другу перпендикулярны? Поясните.

4. В правильной четырехугольной пирамиде боковое ребро образует с плоскостью основания угол 45º. Сторона основания пирамиды равна 6 см. Найдите площадь боковой поверхности пирамиды.

 

Поделиться:

Воспользуйтесь поиском по сайту: