Нормальный закон распределения.

Раздел IV. Элементы теории вероятностей в социологических исследованиях.

Лекция 5. Законы распределения случайных величин в социологических исследованиях.

Цель:

Познакомить с основными законами распределения и их ролью в социологии.

План:

1. Биномиальный закон распределения.

2. Закон распределения Пуассона.

3. Показательный закон распределения.

4. Распределение Ципфа-Парето.

5. Нормальный закон распределения.

 

Биномиальный закон распределения.

Биномиальное распределение применяется при изучении парапсихологических явлений, например телепатии. Случайная величина X называется распределённой по биномиальному закону, если она принимает значения m с вероятностью

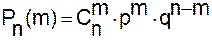, где m=0,1,2,…, n; 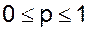и .

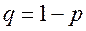Это ДСВ. У неё такой закон распределения.

 

X			…	m	…	n
P	qn	npqn-1	…		…	pn

 

Математическое ожидание и дисперсия данной случайной величины.

M(X)=np D(X)=npq

Пример 1. Производится 3 независимых социологических испытания. При каждом испытании событие А появляется с одной и той же вероятностью p=0,6. Записать в виде таблицы закон распределения случайной величины Х - “числа появлений события А при этих испытаниях”.

Это биномиальное распределение, для которого закон распределения имеет вид:

X
P	q 3	3 pq 2	3 p 2 q	p 3

тогда

X
P	0,064	0,288	0,432	0,216

Контроль: 0,064+0,288+0,432+0,216=1.

Закон распределения Пуассона.

Случайная величина Y называется распределённой по закону Пуассона, если она значение k, принимает с вероятностью

, где . Это ДСВ, характеризующая возможность появления редких событий, с таблицей распределения.

X		…	k	…
P		…		…

Итак, необходимым условием того, что случайная величина распределена по закону Пуассона, является равенство M(x) и D(x).

Пример 2. При введении вакцины против полиомиелита иммунитет создаётся в 99,99% случаев. Какова вероятность того, что из 1000 вакцинированных детей заболеет соответственно 1, 2, 3, 4 ребёнка?

Решение. Вероятность заболеть p=0,0001, число испытаний n=10000, поэтому a=np=1. По формуле 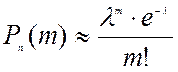находим

Показательный закон распределения.

СВ X, которая может принимать только неотрицательные значения с плотностью , где , Называется распределённой по показательному закону.

Числовые характеристики СВ распределённой по показательному закону: , ,

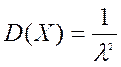Необходимым условием того, что СВ распределена по показательному закону является равенство

По показательному закону распределено время обслуживания, продолжительность ремонта, время простоя в очереди и др.

Вероятность попадания СВ, распределенной по показательному закону

.

Пример 3. Среднее время обслуживания покупателя 10 минут. Чему равна вероятность простоя в очереди от 10 до 20 минут?

Решение. По условию , тогда . если X - время обслуживания, то. .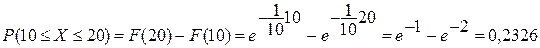

 

4. Распределение Ципфа-Парето (Зипфа-Парето). С.в., имеющая это распределение, принимает значения на полубесконечном интервале , ее функция распределения есть

,

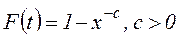а плотность соответственно

.

Такое распределение описывает, например, какая доля жителей страны живет в городах, которые занимают определенное место по численности населения, или какая доля ресурса приходится на носителей (или потребителей) этого ресурса, занимающих определенное место – например, какая доля пива выпивается самыми большими его любителями.

 

Нормальный закон распределения.

В социально-психологических исследованиях чаще всего ссылаются на нормальное распределение, которое играет важнейшую роль в применении численных методов в социологии. Оно лежит в основе измерений, методов проверки гипотез.

Продолжительность жизни, возраст вступления в брак и появление первого ребенка и т. д., подчиняются строгой закономерности. Распределения частот встречаемости любого демографического (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большом количестве людей, имеет одну и ту же колоколообразную форму.

Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются довольно редко, а значения, близкие к средней величине – довольно часто. И продолжительность жизни, и рост человека, и психологические особенности, например, способности,– это случайные проявления, частота встречаемости которых подчинена закону нормального распределения.

Случайная величина X называется распределённой по нормальному закону, если плотность её распределения определяется по формуле:

,

где и - параметры распределения, (положительное действительное число), - любое действительное число. Записывается это так N(a, ).

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Она имеет колоколообразную форму. Это симметричная кривая.

 

Вероятностный смысл параметров: - математическое ожидание, - среднее квадратическое отклонение. Если =0; =1, то получаем стандартное распределение N(0,1), у которого плотность распределения имеет вид:

.

Эта малая функция Лапласа.

С нормальным законом распределения тесно связана функция Лапласа

.

Вероятность того, что случайная величина X, распределена по нормальному закону с параметрами и , примет значение из промежутка , определяется по формуле:

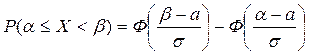
Вероятность отклонения нормальной случайной величины от её математического ожидания определяется по формуле:

, где .

Что же общего у всех нормальных кривых? Чтобы ответить на этот вопрос положим в последнем равенстве , тогда поучим:

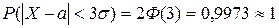
Это правило называется “правило трёх сигма” и оно означает, что среди 10000 значений X только 27 выйдут за пределы интервала 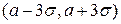и событие является практически достоверным.

В социально - психологических исследованиях нормальное распределение используется в первую очередь при разработке и применении тестов интеллекта и способностей. Психометрические тесты общих и специальных умственных способностей часто дают приблизительно нормальное распределение оценок. Значения IQ интеллектуального теста распределены приблизительно нормально. Имея среднее значение равное 100 для любой конкретной возрастной группы и стандартное отклонение равное 16 у нормальных людей.

Пример 4. Спортсмен каждое утро взвешивается на напольных весах. Случайные ошибки измерения Х веса подчинены нормальному закону со средним квадратическим отклонение, равным 10 мг. Найти вероятность того, что измерение будет произведено с ошибкой меньшей по абсолютной величине 15 мг, если известно, что математическое ожидание случайных ошибок Х равно нулю.

Решение. По формуле находим .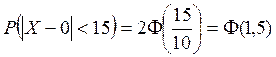

По таблице 2 находим: . Тогда искомая вероятность равна

.

Пример 5. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 30 у.е., и средним квадратическим отклонением, равным 10. Определить вероятность того, что в случайно выбранный день обслуживаемого периода цена за акцию была между 10 и 50 у.е.

Решение. Воспользуемся формулой 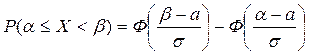. По условию , тогда

По таблице приложения 2 находим . Отсюда, искомая вероятность .

Пример 6. Вес тропического грейпфрута, выращенного в Краснодарском крае – случайная величина, подчиненного нормальному закону с математическим ожиданием 0,5 кг и средним квадратическим отклонением 0,09 кг. Установить: а) вероятность того, что наудачу взятый грейпфрут имеет вес в пределах от 0,4 до 0,7 кг; б) вероятность того, что вес наудачу взятого грейпфрута отличается от математического ожидания не более, чем на 0,2 кг; в) в каких границах следует ожидать вес грейпфрута, чтобы вероятность не выйти за эти границы была равна 0,95.

Решение. а) б) .

в) , тогда .

По таблице 2 имеем , откуда .

Поделиться:

Воспользуйтесь поиском по сайту: