 |
Научный руководитель – Попов О.Н. к.т.н.
|
|
|
|
Средства наружной рекламноЙ информации
Попов О.Н., к.т.н., Моисеенко М.О., к.т.н., Пестряков Е., магистрант
Научный руководитель – Попов О.Н. к.т.н.
Томский государственный архитектурно-строительный университет
Россия, г. Томск
| Рассмотрены вопросы взаимосвязи двух технических дисциплин «Теоретическая механика» и «Сопротивление материалов» Наружная реклама, конструирование, расчет на прочность, проектирование, монтаж, методики расчета. |
Научно-технический прогресс в строительстве и вызванная им необходимость овладения новыми эффективными методами расчета сооружений, приводит к увеличению объема учебного материала, требуемого для подготовки высококвалифицированных специалистов в области расчета и проектирования. Методы расчета сооружений для инженеров-строителей в большом объеме излагаются в курсе строительной механики.
Строительная механика − это наука о расчете сооружений на прочность, жесткость и устойчивость при действии на них статических и динамических нагрузок.
Строительная механика, как и сопротивление материалов, является одним из разделов механики твердых деформируемых тел. В ней широко используются методы теоретической механики, которая изучает равновесие и движение твердых тел, считая их абсолютно твердыми [1].
Существует мнение, что появление мощных универсальных методов должно вытеснить из учебного курса строительной механики традиционные методы анализа сооружений. Однако изучение строительной механики в вузе также преследует цель не только снабдить студента аппаратом для расчета конструкций, но и научить его понимать «игру сил», чувствовать работу различных конструкций под действием различных нагрузок. Это достигается только изучением традиционных методов, при анализе простых конструкций, которые сохраняются в курсе строительной механики. Этого также можно достичь, увязав изложение традиционных методов с излагаемыми разделами в курсе теоретической механики.
|
|
|
В данной статье показывается, какой материал используется при преподавании курса “Строительная механика” из базового курса “Теоретическая механика”. Предполагается, что преподаватель кафедры “Теоретическая механика” (ТМ) при изложении материала учитывает потребность общеинженерной дисциплины “Строительная механика” (СтрМ). В дальнейшем новые знания, полученные студентами ассоциируются с ранее полученными. При этом у студентов появляется стимул к изучению предметов, которые некоторые студенты считают ненужными.
Рассмотрим во взаимосвязи основные темы разделов СтрМ и ТМ.
1. Основные понятия.
1.1. Модель абсолютно твердого тела и способ сечений. В СтрМ принимается принцип затвердения, ввиду малости упругих деформаций по сравнению с размерами тела который применяется при определении опорных реакций и внутренних усилий.
1.2. Разложение силы на равнодействующие В СтрМ мерой внутренних сил является векторная величина − напряжение, которое раскладывается на нормальное и касательное, по правилам ТМ.
1.3. Три формы равновесия: устойчивое, безразличное и неустойчивое (Теорема Лежена − Дирихле). В СтрМ внимание концентрируется на устойчивом равновесии.
1.4. Момент силы относительно оси и лемма о параллельном переносе силы. В СтрМ рассчитываются пружины, которые рассчитываются на действие сдвига и кручение.
1.5. Уравнения равновесия.
1.6. Работа, мощность. Потенциальная энергия. В СтрМ данные понятия применяются при определении линейных и угловых перемещений. К сожалению, в ТМ обычно данные понятия вводятся позже, поэтому в СтрМ применяются знания из физики.
|
|
|
1.7. Основная теорема статики о замене произвольной системы сил. Главный вектор сил и главный вектор момент. В СтрМ, в общем случае, действия произвольной системы сил и внутренних сил в сечении бруса приводятся, по правилам ТМ, к центру тяжести сечения. В результате в качестве статических эквивалентов выступают лишь два векторных силовых фактора: главный вектор и главный вектор-момент. Для удобства решения каждый из векторов раскладывается на составляющие векторы вдоль соответствующих координатных осей. В общем случае получаем шесть внутренних силовых факторов.
1.8. Разложение и сложение векторов. В СтрМ при рассмотрении темы сложный изгиб действующая сила раскладывается на составляющие вдоль координатных осей. Это позволяет рассматривать совокупность двух обычных поперечных изгибов. Рассматривая изгиб от каждой из составляющих силы, определяем прогибы относительно разных осей. Суммируя полученные составляющие прогиба по правилу параллелограмма, получаем прогиб при косом изгибе и по модулю, и по направлению. Оказывается, что прогиб не будет направлен по силовой линии. Аналогично показывается, что нейтральная линия не будет перпендикулярна силовой линии.
1.9. Лемма о параллельном переносе силы. В СтрМ при рассмотрении темы расчет арки рассматривается внецентренное сжатие (растяжение) вектор сила, который параллелен оси бруса. Это действие силы на брус в СтрМ сводится к совокупности ранее изученных деформаций: осевому действую продольной силы и косому изгибу. Такая операция основывается на лемме ТМ о параллельном переносе силы. При этом переносится сила, а вектор момент раскладывается на две составляющие вокруг осей в поперечном сечении.
1.10. Момент силы относительно оси. В СтрМ сложное сопротивление разного характера рассматривается на примере кривого стержня. При этом предварительно строятся эпюры: продольных, поперечных сил возникающих относительно разных осей, крутящих и изгибающих моментов относительно осей поперечных сечений. При построении эпюр применяется понятие о моменте силы относительно оси, которое было введено в ТМ.
2. Многопролетные балки.
|
|
|
2.1. Метод сечений. Поперечная сила − 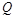 и изгибающий момент −
и изгибающий момент − 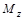 устанавливаются с применением способа сечений и составлением уравнений равновесия. Поперечная сила −
устанавливаются с применением способа сечений и составлением уравнений равновесия. Поперечная сила − 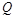 в сечении балки численно равна алгебраической сумме проекций всех сил, действующих на балку по одну сторону от рассматриваемого сечения, на вертикальную ось. Изгибающий момент −
в сечении балки численно равна алгебраической сумме проекций всех сил, действующих на балку по одну сторону от рассматриваемого сечения, на вертикальную ось. Изгибающий момент − 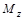 в том же сечении балки численно равен алгебраической сумме моментов всех сил, действующих на балку по одну сторону от рассматриваемого сечения, относительно центра тяжести сечения.
в том же сечении балки численно равен алгебраической сумме моментов всех сил, действующих на балку по одну сторону от рассматриваемого сечения, относительно центра тяжести сечения.
2.2. Линии влияния для многопролетных балок.
График, изображающий закон изменения какого-либо фактора (например, опорной реакции) при передвижении по сооружению силы 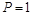 , называется линией влияния этого фактора. Величины опорной реакции −
, называется линией влияния этого фактора. Величины опорной реакции −  , момента −
, момента − 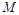 , поперечной силы −
, поперечной силы − 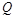 определяются в зависимости от расстояния
определяются в зависимости от расстояния 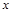 , аналогично как в теоретической механике.
, аналогично как в теоретической механике.
Построение линий влияния кинематическим методом основано на использовании принципа возможных перемещений, изучаемого в курсе теоретической механики. Напомним его формулировку: если механическая система находится в равновесии, то сумма работ всех сил на любых возможных перемещениях равна нулю. Возможные перемещения − бесконечно малые перемещения, допускаемыми связями. Возможные перемещения направлены по касательной к действительной траектории.
2.3. Определение усилий и опорных реакций. Определение искомых величин от действующей нагрузки определяется также согласно принципу возможных работ. Например, возможная работа силы определяется скалярным произведением вектора силы на вектор возможного перемещения. По составленным уравнениям определяются искомые величины.
3. Трехшарнирные арки и рамы. Арочными называются системы криволинейного или ломаного очертания, в опорах которых от вертикальной нагрузки возникают наклонные реакции. Горизонтальная составляющая такой наклонной реакции называется распором.
3.1. Уравнения равновесия. Трехшарнирная арка является системой геометрически неизменяемой и статически определимой. Такие системы изучаются в ТМ.В рассматриваемой теме СтрМ при выводе ряда формул, доказательстве некоторых зависимостей используются уравнения равновесия статики:
|
|
|
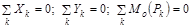 .
.
Так, например, при выводе закона парности касательных напряжений, известных дифференциальных зависимостей 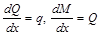 и формулы Журавского
и формулы Журавского 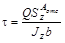 выделяется элемент бесконечно малой длины
выделяется элемент бесконечно малой длины 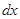 и для него составляются уравнения равновесия.
и для него составляются уравнения равновесия.
3.2. Линии влияния для трехшарнирных арок и рам.
График, изображающий закон изменения какого-либо фактора при передвижении по сооружению силы 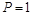 строится, согласно уравнениям аналогичным, как в ТМ в зависимости от ординаты −
строится, согласно уравнениям аналогичным, как в ТМ в зависимости от ординаты − 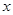 и теоремы о трех силах. Особенностью является учет величины распора −
и теоремы о трех силах. Особенностью является учет величины распора − 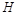 и измени вертикальной координаты −
и измени вертикальной координаты −  и соответствующего положения касательной.
и соответствующего положения касательной.
Построение линий влияния кинематическим методом основано на использовании теоремы о трех силах и принципа возможных перемещений (скоростей), изучаемых в курсе ТМ. Мгновенные центры вращений определяются как мгновенные центры скоростей при плоском движении абсолютно твердых тел.
4. Плоские фермы. Фермой называется стержневая система, остающаяся геометрически неизменяемой после условной замены её жестких узлов шарнирными.
4.1. Определение усилий в стержнях ферм.
Как и в ТМ в СтрМ применяются одинаковые способы при определении усилий в стержнях фермы: вырезания узлов, сквозных сечений (точки Риттера).
4.2. Линии влияния усилий в стержнях ферм.
График, изображающий закон изменения какого-либо фактора при передвижении по сооружению силы 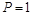 строится, согласно уравнениям аналогичным, как в ТМ, в зависимости от ординаты −
строится, согласно уравнениям аналогичным, как в ТМ, в зависимости от ординаты − 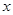 и теоремы о трех силах. Особенностью является учет моментных точек, в отдельных случаях учитывается распор −
и теоремы о трех силах. Особенностью является учет моментных точек, в отдельных случаях учитывается распор − 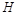 .
.
Построение линий влияния кинематическим методом основано на использовании теоремы о трех силах и принципа возможных перемещений (скоростей), изучаемых в курсе ТМ. Мгновенные центры вращений определяются как мгновенные центры скоростей при плоском движении абсолютно твердых тел.
5. Определение перемещений в упругих системах.
5.1. Принцип возможных работ. В СтрМ для стержневых систем, стержней с ломаной или круговой осью при определении перемещений применяется теорема о взаимности работ и энергетический метод Мора. Они основаны на известном из ТМ принципе возможных перемещений, применяемом для абсолютно жестких тел. В СтрМ рассматриваются деформируемые тела, поэтому уравнение возможных перемещений записывается в виде суммы возможных работ внешней нагрузки − 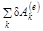 и суммы возможных работ внутренних сил упругости −
и суммы возможных работ внутренних сил упругости − 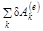 . При этом в СтрМ в качестве возможных, берутся конечные, но малые перемещения, а суммирование заменяется интегрированием.
. При этом в СтрМ в качестве возможных, берутся конечные, но малые перемещения, а суммирование заменяется интегрированием.
|
|
|
При выводе формулы Мора для вычисления перемещений рассматриваются два состояния системы: грузовое (заданное, в котором требуется определить перемещение) и “единичное” − к системе в том месте, где надо определить перемещение, по направлению искомого перемещения прикладывается единичная сила при определении линейного перемещения или единичный момент при определении углового перемещения. Далее применяется принцип возможных перемещений. Равновесная система сил (нагрузок и внутренних сил) берется из “единичного” состояния, а возможные перемещения, в том числе и искомые из заданного состояния.
5.2. Потенциальная энергия. Данное понятие, взятое в ТМ, вводится в СтрМ для вывода в дальнейшем формул при определении перемещений.
5.3. Теоремы о взаимности работ (теорема Бетти) и о взаимности перемещений (теорема Максвелла). Доказательство данных теорем ведется на основании введенного в ТМ понятия работа силы.
6. Статически неопределимые системы.
6.1. Принцип возможных работ с применением обобщенных сил и перемещений.. В СтрМ применяется метод сил, основанный на принципе возможных перемещений, аналогично как в (2.5.1). Статически неопределимую систему превращают в статически определимую, удалив 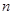 лишних связей и введя вместо них обобщенные искомые силы
лишних связей и введя вместо них обобщенные искомые силы 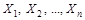 . Обобщенные перемещения, соответствующие силе
. Обобщенные перемещения, соответствующие силе 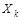 , определяются как сумма двух перемещений. С одной стороны, внешние силы создают обобщенное перемещение −
, определяются как сумма двух перемещений. С одной стороны, внешние силы создают обобщенное перемещение − 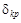 .Также далее рассматривается система под действием одних только лишних обобщенных реактивных сил определяется вызванное ими обобщенное перемещение, равное
.Также далее рассматривается система под действием одних только лишних обобщенных реактивных сил определяется вызванное ими обобщенное перемещение, равное 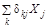 . Согласно принципа возможных перемещений перемещение, соответствующей лишней обобщенной неизвестной равно нулю. Получаем каноническую систему метода сил.
. Согласно принципа возможных перемещений перемещение, соответствующей лишней обобщенной неизвестной равно нулю. Получаем каноническую систему метода сил.
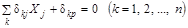 .
.
Системе канонических уравнений можно также дать энергетическое толкование, излагаемое в ТМ. При нагружении статически неопределимой системы лишние (основные) неизвестные имеют такие значения, при которых потенциальная энергия системы является минимальной. В этом состоит так называемый принцип наименьшей работы.
6.2. Метод перемещений. Отрицание реактивных усилий (сил или моментов) во введенных заделках и стержнях основной системы, т.е. отрицание реактивных усилий по направлению неизвестных перемещений, лежит в основе уравнений метода перемещений. В методе перемещений за лишние неизвестные принимаются упругие перемещения. При этом пренебрегается влиянием продольных и поперечных сил на действие стержней, учитываются лишь деформации изгиба. Кроме того, не делается различие между первоначальной длиной прямого стержня и длиной «хорды». Т.е. принимается как в ТМ практически модель абсолютно твердого тела.
7. Тонкостенные оболочки. Толстостенные трубы.
7.1. Уравнения равновесия в полярной системе координат. Рассматриваемые в СтрМ по данной теме оболочки и трубы являются телами вращения, поэтому положение произвольной внутренней точки (элементарного параллелепипеда) удобно рассматривать в полярной системе координат 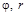 . При осесимметричном нагружении только от одной координаты
. При осесимметричном нагружении только от одной координаты 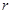 .
.
При определении напряжений в стенке тонкостенной осесиммметричной оболочки под давлением 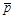 по безмоментной теории: меридиального напряжения −
по безмоментной теории: меридиального напряжения −  и окружного напряжения −
и окружного напряжения − 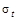 , рассматривается равновесие элементарного элемента оболочки с соответствующими радиусами кривизны
, рассматривается равновесие элементарного элемента оболочки с соответствующими радиусами кривизны 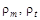 . Так как толщина оболочки −
. Так как толщина оболочки − 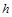 невелика, то напряжения по толщине не изменяются. Получаем уравнение Лапласа.
невелика, то напряжения по толщине не изменяются. Получаем уравнение Лапласа.
При рассмотрении толстостенной трубы также составляются уравнения равновесия, и решается так называемая задача Ламе.
8. Устойчивость сжатых стержней.
8.1. Теорема Лежена − Дирихле. Виды равновесия твердого тела. В ТМ говорится о видах равновесия. При этом при действии продольной нагрузки не допускается изменение прямолинейной формы. При критической силе − 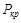 одинаково возможны как прямолинейная, так и криволинейная формы. Имеет место бифуркация, т.е. раздвоение формы равновесия. При устойчивом равновесии сжатого стержня
одинаково возможны как прямолинейная, так и криволинейная формы. Имеет место бифуркация, т.е. раздвоение формы равновесия. При устойчивом равновесии сжатого стержня  .
.
9. Динамическое действие нагрузок.
9.1. Принцип Даламбера. Уравнения кинетостатики. В СтрМ рассматривается расчет движущихся элементов конструкций с ускорением − 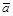 . Согласно принципу Даламбера вводятся силы инерции
. Согласно принципу Даламбера вводятся силы инерции 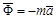 . Составление уравнений равновесия проводится с учетом сил инерции согласно уравнению кинетостатики. В СтрМ подобного типа задачи считаются квазистатическими.
. Составление уравнений равновесия проводится с учетом сил инерции согласно уравнению кинетостатики. В СтрМ подобного типа задачи считаются квазистатическими.
9.2. Закон сохранения механической энергии. В ТМ рассматривается задача о падении груза на пружину с жесткостью − 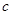 . При решении задачи применяется закон сохранения механической энергии. Перемещение пружины определяется по формуле
. При решении задачи применяется закон сохранения механической энергии. Перемещение пружины определяется по формуле 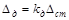 , где
, где  − динамический коэффициент при ударе. В СтрМ применяется точно такая же формула. Разница заключается в определение статического перемещения элементов конструкции в точке соударения.
− динамический коэффициент при ударе. В СтрМ применяется точно такая же формула. Разница заключается в определение статического перемещения элементов конструкции в точке соударения.
9.3. Законы Галилея − Ньютона. В ТМ изучается колебание материальной точки на основе второго закона Ньютона, с помощью которого получаем дифференциальное уравнение второго порядка. После математических преобразований получаем определение выражения амплитуды колебаний 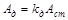 , где
, где 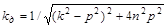 − динамический коэффициент при вынужденных колебаниях В СТРМ применяется точно такая же формула. Разница заключается в определении величин:
− динамический коэффициент при вынужденных колебаниях В СТРМ применяется точно такая же формула. Разница заключается в определении величин: 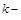 круговой частоты свободных гармонических колебаний,
круговой частоты свободных гармонических колебаний, 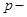 круговой частоты вынужденных колебаний,
круговой частоты вынужденных колебаний, 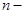 коэффициента затухания.
коэффициента затухания.
10. Расчеты за пределом упругости.
10.1. Уравнения равновесия. Статический момент площади относительно оси. В СтрМ при упругопластическом изгибе стержня вводится понятие пластического шарнира (по всему сечению напряжения достигают предела текучести). При несимметричном сечении определяется положение нейтральной оси, которое определится из условия равновесия. Из которого следует, что площади растянутой и сжатой зон равны. При этом предельный момент определяется через статические моменты площади −  растянутой и сжатой зон сечения
растянутой и сжатой зон сечения 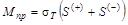 .
.
Заключение.
1. Выше было показано, какие разделы общеобразовательного предмета ТМ применяются в общеинженерной дисциплине СтрМ. Изложенный материал должен использоваться при составлении рабочих программ на кафедре ТМ. Также необходимо учитывать последовательность изложения в зависимости от рабочего плана по СтрМ по соответствующей специальности. Т.е. необходимо взаимоувязывать рабочие планы ведущим преподавателям кафедр СтрМ и ТМ. Это позволит не дублировать при изложении один и тот же материал (например, геометрические характеристики, удар, колебания), взаимоувязывать и показывать связь между предметами. При этом у студентов появляется стимул к изучению предметов, которые некоторые студенты считают ненужными, не вникая в суть изложения предметов. Выше сказанное особенно надо учитывать при уменьшающемся количестве выделяемых часов на изучение курсов СтрМ и ТМ и учете специальности студентов [3].
2. Кроме того, отметим, что должна существовать возможность для поддержания самовоспроизводящейся и развивающейся системы. Что не учитывается в количество выделяемых часов при двухуровневом образовании при изучении ТМ, для выхода на второй уровень (магистратура). А, при изучении СтрМ дополнительные часы не даются на освоение ряда основополагающих понятий.
Список используемой литературы
1. Лачуга, Ю.Ф. Теоретическая механика. М.: Колос С, 2005. − 576 с.
2. Григорьева, Н.А. Междисциплинарное взаимодействие кафедр теоретической механики и строительной механики / Н.А. Григорьева, О.Н. Попов // Пробл. инженерного образования. Мат. регион. НПК − Томск: Изд-во Том. гос. архит.-строит. ун-та. 2010. − С. 32-35.
3. Концентрическая схема изучения предмета − С. 376-377. − В кн.: Теоретическая механика (доп. к общ. разд.) / В.Г. Веретенников, В.А. Синицын − М.: ФИЗМАТЛИТ, 2006.
4. Дарков, А.В. Строительная механика: Учеб. для строит. спец. вузов. − М.: Высш. шк. − 1986. − 607. с.
|
|
|


