 |
Тест 3. Вычисление интегралов.
|
|
|
|
Таблица неопределённых интегралов некоторых функций.
1.) 
| 2.) 
|
3.) 
| 4.) 
|
5.) 
| 6.) 
|
7.) 
| 8.) 
|
9.) 
| 10.) 
|
11.) 
| 12.) 
|
13.) 
| 14.) 
|
15.) 
| 16.) 
|
17.) 
| 18.) 
|
19.) 
| 20.) 
|
21.) 
| 22.) 
|
23.) 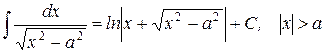
| 24.) 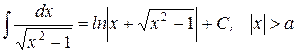
|
25.) 
| 26.) 
|
27.) 
| 28.) 
|
Основные свойства неопределённого интеграла.

| Производная неопределенного интеграла равна подынтегральной функции. |
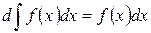
| Дифференциал от неопределенного интеграла равен подынтегральному выражению. |

| Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной. |
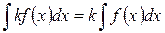
| Постоянный множитель можно вынести из-под знака интеграла, если k = const ¹0. |
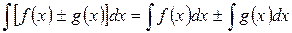
| Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно. |
Основные методы интегрирования.
| Непосредственное интегрирование | Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов. |
| Метод подстановки (метод замены переменной) | Введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т. е. перейти к непосредственному интегрированию:
 или или

|
| Метод интегрирования по частям | Основан на использовании формулы дифференцирования произведения двух функций:

|
Основные свойства определённого интеграла.
Если а = b, то 
| Если а > b, то 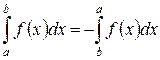
|
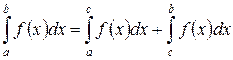
| Каковы бы ни были числа а, b и с, всегда имеет место это равенство |

| Постоянный множитель можно выносить за знак определённого интеграла. |

| Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов. |
Если всюду на отрезке [ а, b] функция f(x)³0, то 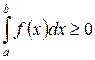
| Если всюду на отрезке [ а, b] функция f(x)³g(x), то 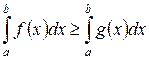
|
Формула Ньютона Лейбница.
|
|
|

Замена переменной в определённом интеграле:

| Интегрирование по частям в определённом интеграле:

|
Связь между дифференцированием и интегрированием:
Простейшая функция

| Дифференциал

| Интеграл


|
1.) 
| 
| 
|
2.) 
| 
| 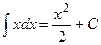
|
3.) 
| 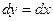
| 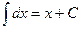
|
4.) 
| 
| 
|
5.) 
| 
| 
|
6.) 
| 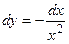
| 
|
7.) 
| 
| 
|
8.) 
| 
| 
|
9.) 
| 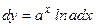
| 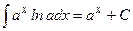
|
10.) 
| 
| 
|
11.) 
| 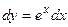
| 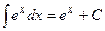
|
12.) 
| 
| 
|
13.) 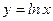
| 
| 
|
14.) 
| 
| 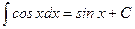
|
15.) 
| 
| 
|
16.) 
| 
| 
|
17.) 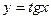
| 
| 
|
18.) 
| 
| 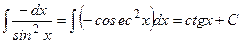
|
19.) 
| 
| 
|
20.) 
| 
| 
|
21.) 
| 
| 
|
22.) 
| 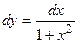
| 
|
23.) 
| 
| 
|
Задание 1. Найти производные и первообразные указанных функций:
| Вычислить производные следующих функций: | Вычислить одну из первообразных следующих функций: |

| 
|
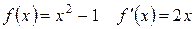
| 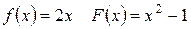
|

| 
|
Вычислить все первообразные следующей функции  (вычислить неопределённый интеграл): (вычислить неопределённый интеграл): 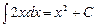 , где С = const. , где С = const.
|
Задание 2. Вычислить неопределённые интегралы:
 , где С = const. , где С = const.
| 
| 
|
 , где С = const. , где С = const.
| 
| 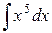
|
 , где С = const. , где С = const.
| 
| 
|
 , где С = const. , где С = const.
| 
| 
|
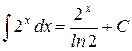 , где С = const. , где С = const.
| 
| 
|
 , где С = const. , где С = const.
| 
| 
|
 , где С = const. , где С = const.
| 
| 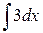
|
Непосредственное интегрирование:
Задание 3. Вычислить неопределённые интегралы. Результаты интегрирования проверить дифференцированием:
| Интегрирование: | Дифференцирование: |

| 
|

| 
|

|
Метод подстановки (метод замены переменной)
1. метод внесения под знак дифференциала:
Задание 4. Вычислить неопределённые интегралы. Результаты интегрирования проверить дифференцированием:
| Интегрирование: | Дифференцирование: |

| 
|

| |

| 
|
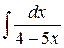
| |

| 
|

| 
|
Метод подстановки (метод замены переменной)
2. непосредственная замена:
Задание 5. Вычислить неопределённые интегралы. Результаты интегрирования проверить дифференцированием:
| Интегрирование: | Дифференцирование: |

| 
|

| 
|
Метод интегрирования по частям
Задание 6. Вычислить неопределённые интегралы. Результаты интегрирования проверит дифференцированием:
|
|
|
| Интегрирование: | Дифференцирование: |

| |

| 
|

|
Интегрирование рациональных функций

Разложим подынтегральную функцию на сумму простейших дробей:
 x 3+1 x 2-3 x +2
x 3+1 x 2-3 x +2
x 3-3 x 2+2 x x +3
3 x 2-2 x +1
3 x 2-9 x +6
7x-5
Получили


Тогда


Разложим подынтегральную функцию на сумму простейших дробей:
 x 3+2 x 2+2 x +4
x 3+2 x 2+2 x +4
x 3+2 x 2+4 x x -2
-2 x 2-4 x +2
-2 x 2-4 x -8

Тогда:

Определённый интеграл
Задание 7. Вычислить определённые интегралы по формуле Ньютона-Лейбница.
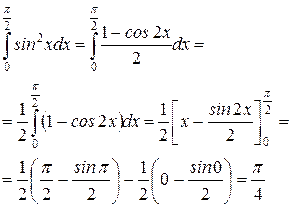
| 
|

| 
|

| 
|
Задание 8. Вычислить площадь фигуры, ограниченной линиями:
у =- х 2+6 х -5 и у = х -5.

|  Ответ:125/6 кв.ед.
Ответ:125/6 кв.ед.
|
у = х 2-2 х -1 и у = х -1

| Ответ: 4,5 кв.ед. |
Тест 3. Вычисление интегралов.
Вопрос 1Вычислить неопределённый интеграл 
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 2Вычислить неопределённый интеграл 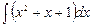
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 3Вычислить неопределённый интеграл 
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 4Вычислить неопределённый интеграл 
| |||
а.) 
| б.) 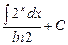
| в.) 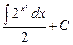
| г.) |
Вопрос 5Вычислить неопределённый интеграл 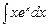
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 6Вычислить неопределённый интеграл 
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 7Вычислить неопределённый интеграл 
| |||
а.) 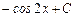
| б.) 
| в.) 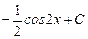
| г.) |
Вопрос 8Вычислить неопределённый интеграл 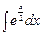
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 9Вычислить неопределённый интеграл 
| |||
а.) 
| б.) 
| в.) 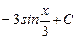
| г.) |
Вопрос 10Вычислить неопределённый интеграл 
| |||
а.) 
| б.) 
| в.) 
| г.) |
Вопрос 11Вычислить определённый интеграл 
| |||
| а.) 0,5 | б.) 1 | в.) 2 | г.) |
Вопрос 12Вычислить определённый интеграл 
| |||
| а.) ¥ | б.) 3 | в.) 1 | г.) |
Вопрос 13Вычислить определённый интеграл 
| |||
| а.) 2 | б.) 4 | в.) 6 | г.) |
Вопрос 14Вычислить определённый интеграл 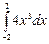
| |||
| а.) 16 | б.) 0 | в.) 32 | г.) |
Вопрос 15Вычислить определённый интеграл 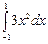
| |||
| а.) 1 | б.) 2 | в.) 0 | г.) |
|
|
|


