Основные положения выборочных испытаний. Методы формирования выработок.

Логарифмически нормальное распределение

Говорят, что случайная величинаY имеет логарифмически нормальное распределение (сокращённо логнормальное распределение), если её логарифмlnY=X распределён нормально, то есть если

где величина X имеет нормальное распределение с параметрами Плотность логнормального распределения задаётся формулой

Математическое ожидание и дисперсию логнормального распределения определяют по формулам

Логарифмически нормальное распределение встречается в ряде технических задач. Оно даёт распределение размеров частиц при дроблении, содержаний элементов в минералах в извержённых горных пародах, численности рыб в море и т.д. Встречается такое распределение во всех задачах, где логарифм рассматриваемой величины можно представить в виде суммы большого количества независимых равномерно малых величин:

то есть , где независимы.

Распределение Вейбула

Случайная величина X подчиняется закону распределения Вейбула с параметрами , если её плотность распределения вероятностей записывается в виде

Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид: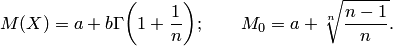

Распределение Вейбула в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике.

Распределение хи-квадрат

Частный случай гамма-распределения с параметрами и называется распределением хи-квадрат с n степенями свободы (пишут ). Если случайная величина X подчиняется закону , то её плотность распределения вероятностей есть

Основные хар-ки распределение хи квадрат (матем ожидание и дисперсия):

№15

В математике компози́ция фу́нкций — это применение одной функции к результату другой. Композиция функцийG и F обычно обозначаетсяGoF, что означает применение функцииG к результату функцииF.

Пусть и две функции. Тогда их композицией называется функция 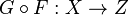, определённая равенством:

.

Свойства композиции

Композиция ассоциативна: .

Если 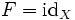— тождественное отображение на X, то есть ,

То .

Если — тождественное отображение на Y, то есть ,то .

Рассмотрим пространство всех биекций множества X на себя и обозначим его . То есть если , то — биекция. Тогда композиция функций из является бинарной операцией, а — группой. является нейтральным элементом этой группы. Обратным к элементу является — обратная функция.Группа , вообще говоря, не коммутативна, то есть .

№16

1. Значения функции распределения вероятностей принадлежат отрезку [0,1]: 0≤F(x)≤1.
2. Функция распределения вероятностей – неубывающая функция, то есть: , если .
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b), равна приращению функции распределения вероятностей на этом интервале:
.
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, =0.Используя последнее следствие, легко убедиться в справедливости следующих равенств:
3. Если возможные значения непрерывной случайной величины принадлежат интервалу (a, b), то:F(x)=0 если x≤a, F(x)=1 если x≤b.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
; .
Плотностью распределения вероятностей непрерывной случайной величиныX называют функциюf(x) – первую производную от функции распределения вероятностейF(x).
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
Теорема. Вероятность того, что непрерывная случайная величинаX примет значение, принадлежащее интервалу (a, b),

равна определенному интегралу от плотности распределения,

взятому в соответствующих пределах: .

Следовательно, зная плотность распределения вероятностиf(x), можно найти функцию распределенияF(x) по формуле
.

Свойства плотности распределения вероятностей

1. Плотность распределения вероятностей – неотрицательная функция:f(x)≥0..

2. Несобственный интеграл от плотности распределения вероятностей в пределах от -∞ до +∞ равен единице:

Вероятностный смысл плотности распределения вероятности. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (x, x+∆x), приближенно равна (с точностью до бесконечно малых высшего порядка относительно ∆x) произведению плотности распределения вероятности в точке на длину интервала∆x:
.

Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величиныX, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл
, или - для всей числовой оси.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные непрерывной случайной величиныX принадлежат отрезку[a,b], то
,или - для всей числовой оси.Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии: .

№17

Надёжность изделий определяется набором показателей; для каждого из типов изделий существуют рекомендации по выбору показателей Надёжность Для оценки Надёжность изделий, которые могут находиться в двух возможных состояниях – работоспособном и отказовом, применяются следующие показатели: среднее время работы до возникновения отказа Тср – наработка до первого отказа; среднее время работы, приходящееся на один отказ, Т – наработка на отказ; интенсивность отказов l(t); параметр потока отказовw(t); среднее время восстановления работоспособного состояния tв; вероятность безотказной работы за время t [Р (t)]; готовности коэффициент Kr.

Закон распределения наработки до отказа определяет количественные показатели Надёжность невосстанавливаемых изделий. Закон распределения записывается либо в дифференциальной форме плотности вероятности f (t), либо в интегральной форме F (t). Существуют следующие соотношения между показателями Надёжность и законом распределения:

Для восстанавливаемых изделий вероятность появления n отказов за время t в случае простейшего потока отказов определяется законом Пуассона:

Из него следует, что вероятность отсутствия отказов за время t равна Р (t) = exp(-lt) (экспоненциальный закон надёжности).

Технические системы, состоящие из конструктивно независимых узлов, обладающие способностью перестраивать свою структуру для сохранения работоспособности при отказе отдельных частей, в теории Надёжность принято называть сложными техническими системами (в отличие от сложных кибернетических систем, называются также большими системами). Число работоспособных состоянии таких систем – два и более. Каждое из работоспособных состояний характеризуется своей эффективностью работы, которая может измеряться производительностью, вероятностью выполнения поставленной задачи и т.д. Показателем Надёжность сложной системы может быть суммарная вероятность работоспособности системы – сумма вероятностей всех работоспособных состояний системы.

 

№18

 

 

№19

№20

Комплексные показатели надежности используются для эксплуатационной оценки надежности восстанавливаемых систем изделий.

№21

Под структурной схемой надежности понимается наглядное представление (графическое или в виде логических уравнений) условий, при которых работает или не работает исследуемый объект (система, устройство, техкомплекс). Простейшей формой структурной схемы надежности является параллельно-последовательная структура. На ней параллельно соединяются элементы, совместный отказ которых приводит к отказу объекта.Структурная надежность – это результирующая надежность при заданной структуре и известных значениях надежности всех входящих в нее блоков или элементов.

Структурные методы являются основными методами расчета показателей надежности в процессе проектирования объектов, поддающихся разукрупнению на элементы, характеристики надежности, которых в момент проведения расчетов известны или могут быть определены другими методами. Расчет показателей надежности структурными методами в общем случае включает:представление объекта в виде структурной схемы, описывающей логические соотношения между состояниями элементов и объекта в целом с учетом структурно-функциональных связей и взаимодействия элементов, принятой стратегии обслуживания, видов и способов резервирования и других факторов;описание построенной структурной схемы надежности объекта адекватной математической моделью, позволяющей в рамках введенных предположений и допущений вычислить показатели надежности объекта по данным о надежности его элементов в рассматриваемых условиях применения.В качестве структурных схем надежности могут применяться:схемы функциональной целостности;структурные блок-схемы надежности;деревья отказов;графы состояний и переходов.

№22

Априорным анализом надежности и обычно проводится на стадии проектирования ТС. Этот анализ – априори предполагает известными количественные характеристики надежности всех используемых элементов системы. Для элементов, у кот еще нет достаточных количественных хар-к надежности, их задают по аналогии с хар-ками применяющихся аналогичных элементов. Т.о., априорный анализ базируется на априорных (вероятностных) хар-ках надежности, которые лишь приблизительно отражают действительные процессы в аппаратуре ТС. Тем не менее, этот анализ позволяет на стадии проектирования выявить слабые с точки зрения надежности места в конструкции, принять необходимые меры к их устранению, а так же отвернуть неудовлетворительные варианты построения ТС. Поэтому априорный анализ (или расчет) надежности имеет существенное значение в практике проектирования ТС и составл неотъемлемую часть технических проектов.

№23

Прикидочный расчет основывается на следующих допущениях:· все элементы изделия равно надёжны;

· опасности отказов всех элементов изделия не зависят от времени, т. е. λi=const;· отказ любого элемента приводит к отказу всего изделия.Прикидочный расчет надежности применяется в следующих случаях:1) при проверке требований по надежности, выдвинутых заказчиком в техническом задании (ТЗ) на проектирование изделия;2) при расчете нормативных данных по надежности отдельных блоков, устройств и приборов системы (расчет норм надежности отдельных частей системы);3) для определения минимально допустимого уровня надежности элементов проектируемого изделия;4) при сравнительной оценке надежности отдельных вариантов изделия на этапах эскизного проектирования.Прикидочный расчет надежности позволяет судить о принципиальной возможности обеспечения требуемой надежности изделия.Характеристики надежности рассчитываются по вышеприведенным формулам, при этом λс=N∙λэкв., где λэкв. – эквивалентное значение интенсивности отказов элементов, входящих в изделие.

№24

Ориентировочный расчет надежности учитывает влияние на надежность только количества и типов примененных элементов и основывается на след допущениях:все элементы данного типа равнонадежны, т. е. величины интенсивности отказов (λi) для этих эл-тов одинаковы;все эл-ты работают в номинальном (норм) режиме, предусмотренном техусловиями;интенсивности отказов всех элементов не зависят от времени, следовательно, λi(t)=const;· отказы элементов изделия являются событиями случайными и независимыми;· все элементы изделия работают одновременно.

Для определения надежности изделия необходимо знать:1) вид соединения элементов расчета надежности;

2) типы элементов, входящих в изделие, и число элементов каждого типа;3) величины интенсивности отказов элементов λi, входящие в изделие. Выбор λi для каждого типа элементов производится по соответствующим таблицам. Т.о., при ориентировочном расчете надежности достаточно знать структуру системы, номенклатуру примененных элементов и их количество.Ориентировочный метод расчета надежности используется на этапе эскизного проектирования после разработки принципиальных электрических схем изделий.

Этот расчет позволяет определить рациональный состав элементов изделий и наметить пути повышения надежности изделия на стадии эскизного проектирования и проводится по формулам, приведенным выше.

№25

Окончательный расчет надежности изделия выполняется тогда, когда известны реальные режимы работы элементов после испытания в лабораторных условиях макетов и основных узлов изделия

Элементы изделия находятся обычно в различных режимах работы, сильно отличающихся от номинальной величины. Это влияет на надежность как изделия в целом, так и отдельных его составляющих частей. Выполнение окончательного расчета надежности возможно только при наличии данных о коэффициентах нагрузки отдельных элементов и при наличии графиков зависимости интенсивности отказов элементов от их электрической нагрузки, температуры окружающей среды и других факторов, т. е. для окончательного расчета необходимо знать зависимостиλс = ƒ(Кн, Т0, …). Для определения надежности изделия необходимо знать:

1) число элементов с разбивкой их по типам и режимам работы;2) зависимости интенсивности отказов элементов λi от электрического режима работы и заданных внешних условий;3) структуру системы.

В общем случае λi зависит от следующих воздействующих факторов: электрического режима работы данного элемента; окружающей температуры; вибрационных воздействий; механических ударов; линейных ускорений; влажности; воздействия биологических факторов (грибок, плесень, насекомые); давления; облучения и ряда других возможных факторов.

При разработке и изготовлении элементов обычно предусматриваются определенные «нормальные» условия работы: температура +25±100С, номинальный электрический режим, относительная влажность 60±20%, отсутствие механических перегрузок и т. д. Интенсивность отказов элементов в номинальном режиме эксплуатации называется номинальной интенсивностью отказов λ0i.

Интенсивность отказов элементов при эксплуатации в реальных условиях λi равна номинальной интенсивности отказов λ0i, умноженной на поправочные коэффициенты αi и ki. Поправочный коэффициент интенсивности отказов αi = ƒ(t0, Кн) учитывает влияние окружающей температуры и электрической нагрузки, поправочный коэффициент интенсивности отказов ki = ƒ(j, φ) – тип воздействия, главным образом механические перегрузки и относительную влажность окружающего воздуха.Окончательный расчет надежности применяется на этапе технического проектирования изделия. При расчете изделие расчленяется на отдельные конструктивно самостоятельные части. Расчет производится последовательно от простого сложному.

 

 

№26

Резервированием называют метод повышения надежности объекта путем введения избыточности. Задача введения избыточности – обеспечить нормальное функционирование системы после возникновения отказов в ее элементах.

Резервирование может быть структурным, информационным, временным, программным. Информационное резервирование предусматривает использование избыточной информации.

Временное резервирование – использование избыточного времени. Программное резервирование – избыточных программ.

По способам резервирование может быть общим и раздельным

Общее резервирование - резервируется весь объект, аппарат или система в целом

 

Раздельное резервирование - резервируются отдельные элементы системы. Раздельное резервирование выгодно при большом числе аппаратов и увеличении кратности.

№27

Схемы отмеченных способов резервирования приведены на рис. 4-1—4-9. Практическая реализация резервирования для большинства функциональных узлов систем управления не вызывает существенных трудностей. Наибольшую сложность представляет выбор способов резервирования блоков и элементов замкнутых систем. В этих случаях вопросы резервирования необходимо рассматривать и решать одновременно с исследованием динамических свойств системы управления, так как возможное при резервировании изменение параметров системы может привести к потере устойчивости.~~При общем постоянном резервировании с целой кратностью резервируется вся система управления, состоящая из N функциональных узлов (блоков), рис. 4-1. Этот же вид резервирования используется и для отдельного функционального узла (блока), состоящего из п соединенных элементов. В обоих случаях методы анализа надежности идентичны.

Общее постоянное резервирование с целой кратностью. Вероятность отказа Qp параллельно работающих т элементов при r = 1 определяется выражением (3.2), откуда для равно надёжных элементов

; . (3.8)

Чем меньше вероятность отказа каждого из элементов, тем выше эффективность постоянного резервирования. Так, если q = 0,1 и 0,01, а k = 1, то выигрыш в снижении вероятности отказа при резервировании составит соответственно 10 и 100. Рассмотрим связь показателей надежности группы резервированных элементов, кратности резервирования k и длительности работы элементов t при экспоненциальном законе распределения времени их безотказной работы. Если интенсивность отказов каждого из элементов , то согласно (1.12), (1.21), (1.22) имеем

; ; (3.9)

;

;

; .

Графики изменения PP(t/ ) и р(t/ )/ в зависимости от кратности резервирования и длительности работы системы представлены на рис. 3.7. Они показывают, что постоянное резервирование эффективно на начальном участке работы системы, когда t .

№28

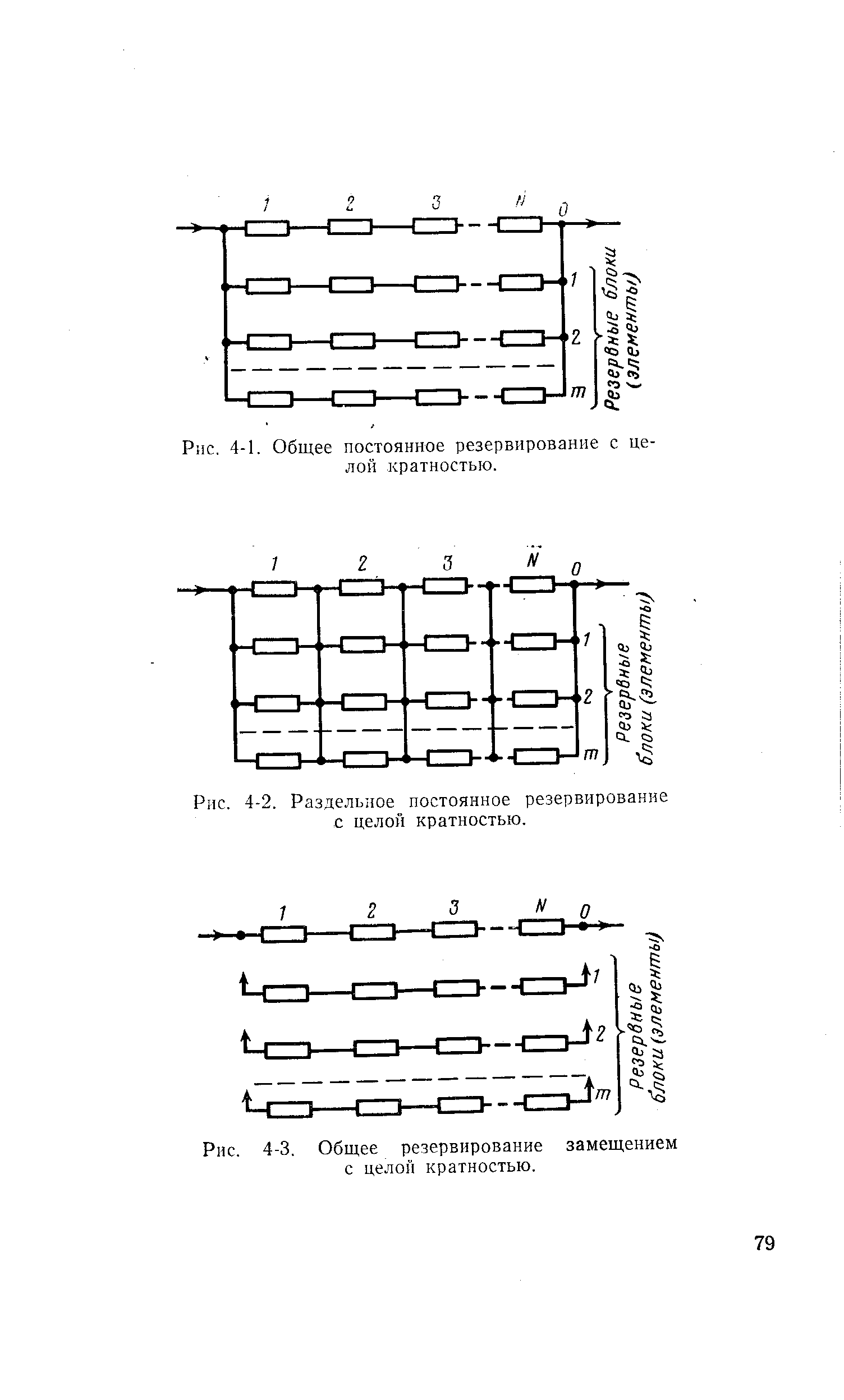Рассмотрим количественные характеристики надежности при раздельном (блочном, поэлементном) постоянном резервировании с целой кратностью (рис. (4-2). Учитывая, что математические выражения для анализа надежности при блочном и поэлементном резервировании идентичны, ниже речь будет идти о поэлементном резервировании.

Раздельное резервирование с постоянно включенным резервом и с целой кратностью (рис. 3.2,6):

(3,4)

где p i (t) — вероятность безотказной работы i -го эле­мента; m i —кратность резервирования i -го элемента; п — число элементов основной системы.

При экспоненциальном законе надежности, когда

(3,5)

При равнонадежных элементах и одинаковой кратности их резервирования

(3,6)

Т ср с = (3,7)

где v i =(i +1)/(m +1 l). Теория атома водорода по Бору Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем - систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга.

№29

В электроснабжении широко используется метод повышения надежности системы за счет использования резервной цепи, находящейся в ненагруженном состоянии. Последняя автоматически включается при отказе основной цепи. Опираясь на результаты, описанные в подразделе 6.1, проанализируем только вариант дублирования замещением, так как в большинстве случаев на практике оказывается достаточно одной резервной цепи (в трансформаторных подстанциях, линиях электропередачи, кабельных линиях).

Предположим, что приборы, обнаруживающие отказ основной цепи, и выключатели, отключающие отказавшую цепь и включающие резервную, также абсолютно надежны. Резервная ненагруженная цепь, находящаяся в режиме ожидания, своих характеристик не меняет и работоспособна. Каждая из цепей состоит из n последовательных элементов (рис. 6.7). Поток отказов простейший.

Учитывая, что анализируемая система (схема) приобретает вид, изображенный на рис. 6.8.

Рассмотрим события, которые могут произойти с системой на отрезке времени t. Проанализируем возможные гипотезы.

Основная цепь отработала успешно все время t и резервную цепь (1) включать не потребовалось. Вероятность этого режима работы системы - Ро(t).

Основная цепь отработала только отрезок  и отказала. При этом сразу же включилась резервная цепь и успешно проработала до конца времени t с вероятностью безотказной работы Р1(t - ).

Чтобы заработал второй режим необходимо совпадение двух событий - отказ основной цепи и успешная работа включенной под нагрузку резервной цепи. Математической оценкой совпадения этих событий является произведение их вероятностей. На рис. 6.9 изображен график плотности вероятности появления отказа основной цепи fo(t). Выделим достаточно малый интервал d, следующий за отрезком . Произведение fo()  d= qо(d). Заштрихованная площадка, численно равна вероятности отказа основной цепи на интервале d. Выражение Р1(t - )  fo()  dпредставляет собой математическую оценку факта отказа основной цепи и успешного вхождения в работу резервной цепи в момент (t - ).

Рис. 6.10. График функции  (t) системы дублированной замещением

(- - - нагруженное дублирование)

В соответствии с формулой полной вероятности [11] вероятность безотказной работы анализируемой системы в течение времени t определяется по выражению:

,где P1/0(t, ) - вероятность безотказной работы цепи "1" в течение времени t при условии, что отказ основной цепи "0" произошел в момент  (на интервале  ). Исходя из условия, что резервная цепь "1" до момента включения своей надежности не теряет, то есть работоспособна, а отказ основной цепи с последующим мгновенным включением резервной цепи может произойти на интервале от 0 до t. . (6.16)

Таким образом, учитывая обе гипотезы, на основе формулы полной вероятности запишем выражение вероятности безотказной работы системы . (6.17)

Зная, что

,

Получим ; (6.18) , (6.19)

а интенсивность отказов системы .

Используя выражение (6.18) после некоторых преобразований, получим . (6.20)

На рис. 6.10 изображен график интенсивности отказов системы, дублированный по способу замещения. Из формулы (6.20) видно, как эта функция монотонно возрастает от до .

В первоначальный момент времени интенсивность отказов дублированной системы, очень низкая . Если такую дублированную систему включить на длительный срок, то выигрыш в надежности уменьшается. Это легко объясняется тем, что с увеличением времени возрастает вероятность отказа основной цепи. При ее отказе вводится в работу резервная цепь с интенсивностью отказов 0.

Сравнивая графики  (t) для систем нагруженного дублирования (рис. 6.5), и дублирование замещением (рис. 6.10), видим, что они похожи друг на друга: на начальном этапе работы надежность их высока. На практике важно знать какой из схем следует отдать предпочтение. Для этого построим график, на котором изображены кривые P(t) системы при различных способах дублирования (рис. 6.11).

На интервале обе схемы, нагруженного дублирования и дублирования замещением, при одном и том же оборудовании по уровню надежности практически идентичны. В практических условиях эту разницу ощутить очень трудно. Так, если средняя наработка до отказа основной цепи To = 5 годам и время рабочего цикла до планового отключения системы составляет t = 0,25 года (один раз в квартал), то 1/год. При этом вероятность безотказной работы схемы нагруженного дублирования Р(0,25) = 0,9987, а вероятность безотказной работы схемы дублирования замещением составит Р(0,25) = 0,999.

В этих условиях выбор схемы включения системы может определить экономический фактор. К примеру, в схеме электроснабжения потребителя используется два кабеля из расчета
100%-го резерва. В начале и конце каждой цепи включены выключатели, отключающие соответствующий отказавший (пробитый) кабель с обеих сторон. При схеме нагруженного дублирования потеря мощности в кабелях составит ,

где i - ток потребителя; R - сопротивление цепи одного кабеля.

В схеме дублирования замещением 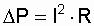, то есть потери мощности в два раза больше. Таким образом, при практически одинаковом значении вероятностей безотказной работы обоих схем в пределах выбранного цикла наработки до планового отключения, вторая схема дублирования замещением экономически не выгодна.

В заключение отметим, что если возникнет необходимость оценки надежности системы, включенной по схеме общего резервирования замещением с целой кратностью, при m > 1 (см. рис. 6.12), то следует пользоваться расчетными формулами [13, 15]:

,где .

 

По способу выполнения резервирование замещением может быть общим и раздельным (рис. 4-3, 4-4). Так как большинство элементов систем управления не требует предварительного прогрева перед включением в работу, рассмотрим свойства резервирования замещением для случая ненагруженного состояния резерва.

№30

Раздельное резервирование замещением с целой кратностью (рис. 3.2, г): (3,13)

где p i (t) —вероятность безотказной работы системы из-за отказов элементов i -го типа, резервированных по способу замещения. Вычисляется P i (t) по формулам общего резервирования замещением.

Надежность системы при раздельном резервировании и с целой кратностью по всем элементам

Расчетная схема надежности для этого случая изображена на рис. 6.13.

Отказ этой системы может произойти при отказе любого блока. Совпадение работоспособных состояний n блоков системы гарантирует работоспособное состояние системы. Следовательно, если известны вероятности безотказной работы каждого из блоков, то вероятность безотказной работы системы выражается формулой

. (6.21)

Воспользуемся результатом расчетов в подразд. 6.1 (см. рис. 6.2). При преобразовании схемы (рис. 6.2) в более удобную схему (рис. 6.14) вероятность безотказной работы каждой из цепей определяется по формуле (6.1). Для элементов схемы (рис. 6.14) принято: ; ; .

Сравнивая структуру одного блока схемы по рис. 6.13 и 6.14 видим, что они идентичны. Следовательно, вероятность безотказной работы системы при раздельном резервировании с целой кратностью определится по выражению произведения вероятностей безотказной работы блоков: ,

где - интенсивность отказов основного элемента K-го блока; выражение в фигурных скобках - вероятность безотказной работы K-го блока.

Среднее время наработки до отказа соответственно найдется по выражению

.При равнонадежных элементах и одинаковой кратности их резервирования по всем блокам [13, 15] расчетные выражения оценки важнейших показателей надежности такой системы примут вид: , (6.23)где = const для всех элементов системы.

, где .

 

 

6.5. Смешанное резервирование неремонтируемых систем

На практике очень часто приходится повышать надежность отдельных элементов (объектов) системы различными способами резервирования, руководствуясь не только задачами надежности, но и экономическими задачами. Этот способ резервирования проанализируем на конкретном примере. Пусть задана схема (система) электроснабжения потребителя (см. рис. 6.15), собранная по основной схеме (одноцепная схема электроснабжения).

Такая система не обеспечивает требуемого уровня надежности электроснабжения потребителя за заданное время t. По одному из вариантов повышения надежности предлагается повысить надежность системы поблочно: в блоке кабелей используется нагруженное дублирование, на трансформаторной подстанции - дублирование замещением (см. рис. 6.16) в блоке ВЛ - нагруженное дублирование. Предполагается, что надежность выключателей значительно выше ВЛ, кабелей и трансформаторов. Принимаем вероятность безотказной работы выключателей равной единице. Резервирование ВЛ выполнено элементами с разными показателями. Требуется составить расчетное выражение, по оценке надежности системы электроснабжения.

Сформулируем понятие отказа. Данная система будет работоспособна, если совпадут работоспособные состояния всех трех блоков: ВЛ, трансформаторной подстанции и блока кабелей. Расчетная схема представлена на рис. 6.17. Следовательно, вероятность безотказной работы этой системы

где ; .

Поскольку в блоке 1 и имеют разные характеристики надежности, то вероятность безотказной работы этого блока по стандартной формуле (6.13) определять нельзя. Следует воспользоваться другими формулами. Блок 1 откажет, если совпадут отказы обоих цепей:

,

следовательно

.

Таким образом, ,

а средняя наработка до отказа .

 

№31

Для резервирования систем или отдельных функциональных цепочек, составленных из однотипных элементов (блоков), можно использовать сравнительно небольшое число резервных элементов, включаемых в работу взамен отказавших. Такое резервирование называется скользящим (рис. 4-9).

№32

Общее резервирование с дробной кратностью и по­стоянно вк

Поделиться:

Воспользуйтесь поиском по сайту: