 |
Запишем степень интеграла в виде произведения интегралов
|
|
|
|
Оценка параметров нелинейного статического ОУ
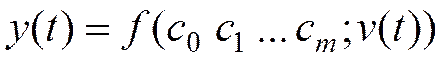 (1)
(1)
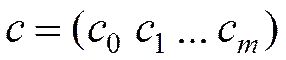
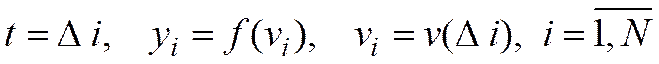
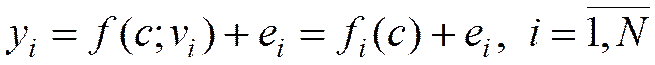 (2)
(2)
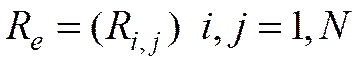
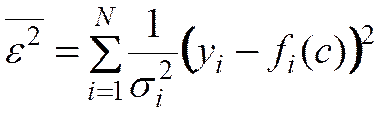 (3)
(3)
Пусть известна грубая оценка  ,
,
Тогда 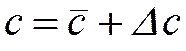
 (4)
(4)
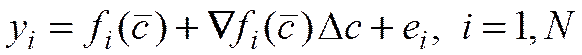 (5)
(5)
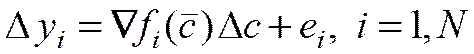 , (6)
, (6)
где  .
.
 , (7)
, (7)
где 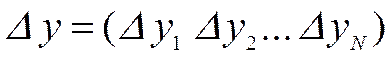 ,
,
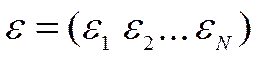 ,
,
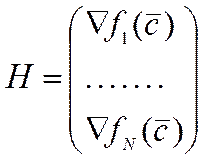 .
.
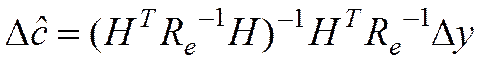 (8)
(8)
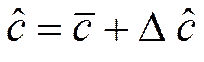
Идентификация нелинейных инерционных ОУ
Постановка задачи
Модель ОУ - Нелинейное дифференциальное уравнение
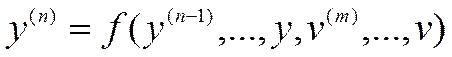 , (1)
, (1)
где 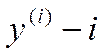 - производная выхода;
- производная выхода;
 - производная входа;
- производная входа;
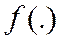 – нелинейная скалярная функция, подлежащая идентификации по наблюдениям входа и выхода объекта
– нелинейная скалярная функция, подлежащая идентификации по наблюдениям входа и выхода объекта 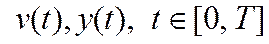 .
.
Модель Вольтерра. Эта модель связана с рядом Вольтерра, которым представляется выход нелинейного динамического объекта.
y[v(t)] 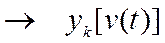 , при k→∞ сколь угодно точно аппроксимирует y[v(t)]
, при k→∞ сколь угодно точно аппроксимирует y[v(t)]
Аппроксимирующая последовательность имеет вид
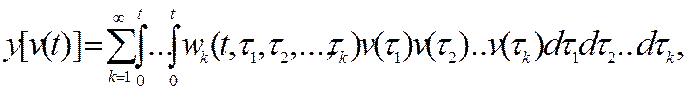 (2)
(2)
где ряд (2) называется функциональным рядом Вольтерра,
Ряд Вольтерра для стационарных объектов
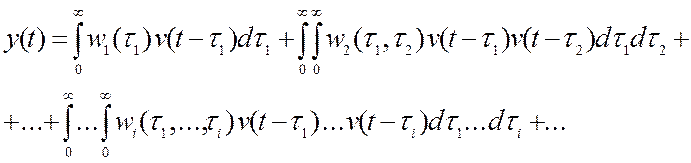 (3)
(3)
Или более компактно
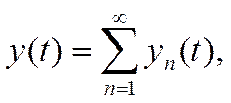 (4)
(4)
где
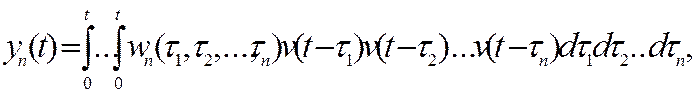 (5)
(5)
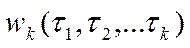 - многомерные импульсные переходные функции объекта (ядра Вольтерра).
- многомерные импульсные переходные функции объекта (ядра Вольтерра).
Совокупность ядер ряда однозначно определяет динамические свойства нелинейного объекта.
Структурная схема нелинейной стационарной системы, описываемой функциональными рядами Вольтерра, может быть представлена в виде
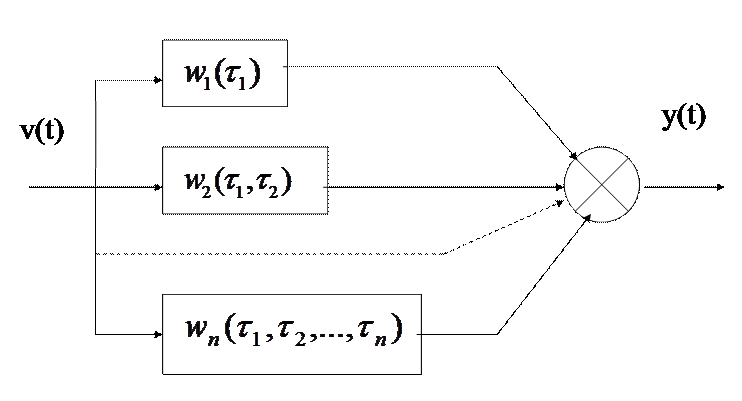
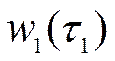 - ядро первого порядка,
- ядро первого порядка,
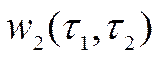 - ядро второго порядка,
- ядро второго порядка,
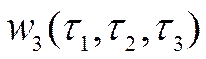 - ядро Вольтерра третьего порядка
- ядро Вольтерра третьего порядка
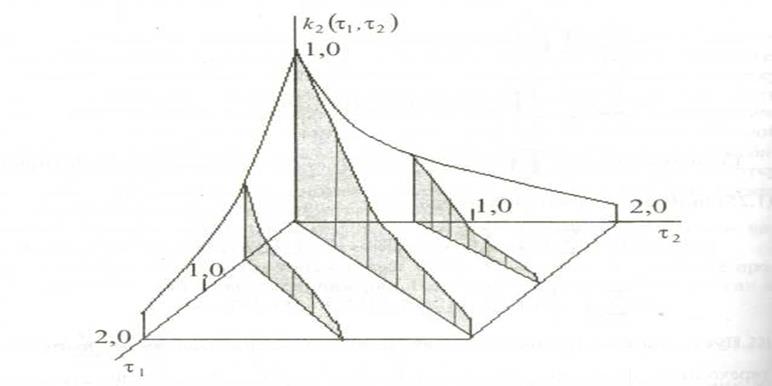
Рис. Импульсная переходная функция 2-го порядка
Если 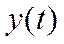 - выход ОУ, то ряд (4), (5) описывает модель этого ОУ
- выход ОУ, то ряд (4), (5) описывает модель этого ОУ
 (6)
(6)
1) 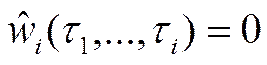 , если
, если 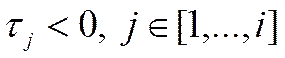
2) 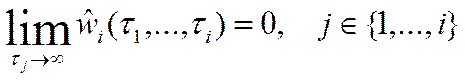
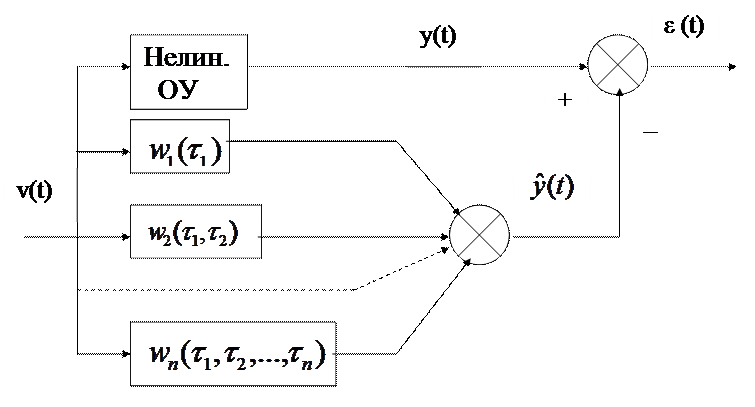
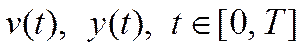
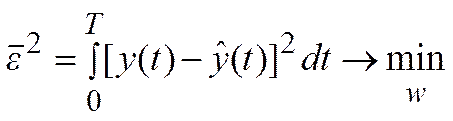 (7)
(7)
Задача идентификации нелинейного ОУ заключается в выборе тестовых воздействий 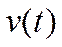 , который позволял бы по измеренным значениям выхода оценивать ядра
, который позволял бы по измеренным значениям выхода оценивать ядра 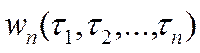 в (6)
в (6)
|
|
|
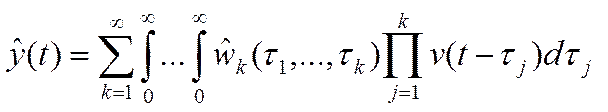 (8)
(8)
1. Выбор амплитуды входного воздействия
2. Влияние соседних членов ряда Вольтерра на точность идентификации ядра  - порядка
- порядка
Рассмотрим один из приемов оценки ядер. Его идея заключается в конструировании из реакций НОУ такого выражения, которое было бы с определенной точностью равно m - слагаемому ряда Вольтерра (8)
Пусть v(t) - вход стационарного нелинейного ОУ. Сформируем воздействия: 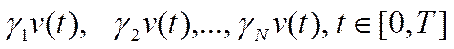
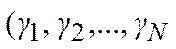 - различные вещественные числа, не равные нулю и соответствующие амплитудам входа
- различные вещественные числа, не равные нулю и соответствующие амплитудам входа 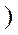

Измеряем реакции ОУ у[γrv(t)] r=1,…,N.
 (9)
(9)
где b r - вещественные числа, которые выбираются следующим образом:
Подставим (8) в (9)
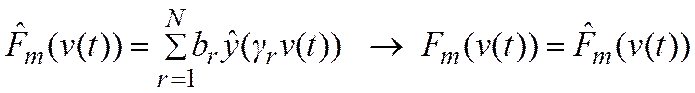 (10a)
(10a)
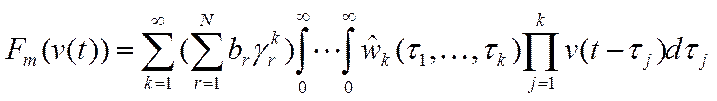 (10)
(10)
Выберем числа br таким образом, чтобы в правой части (10) обратились в нуль все N членов, кроме m-го, а коэффициент при m-кратном интеграле стал равным единице 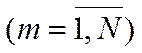
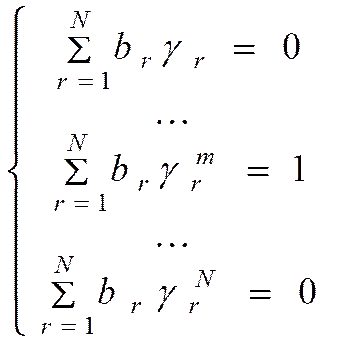 (11)
(11)
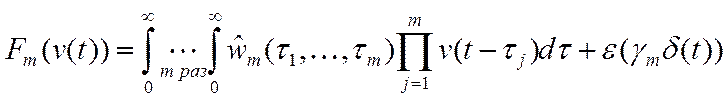
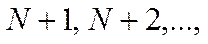
Алгоритм:
· Вход 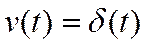 ;
;
· выбираем амплитуды входа 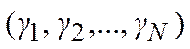 для эксперимента;
для эксперимента;
· находим коэффициенты 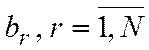 из условия (11);
из условия (11);
· проводим активный эксперимент, в результате которого фиксируем реакции нелинейного ОУ на входы 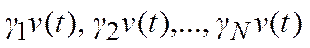 и вычисляем последовательно
и вычисляем последовательно 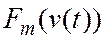 (9);
(9);
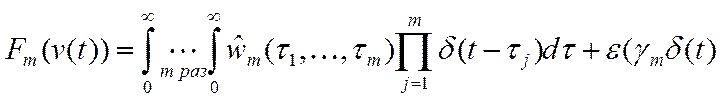
· 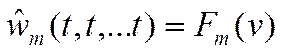
Пример. Для ядра 1-го порядка
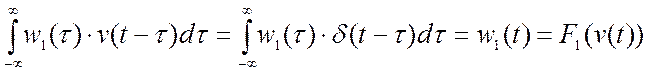 . (12)
. (12)
Подобным образом находим ядро второго порядка, положив
v(t)=d(t)
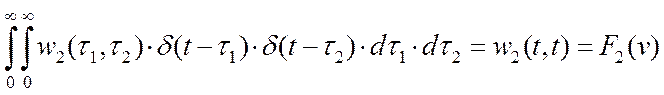 и т.д.
и т.д.
Параметризация задачи, т. е. представление функции 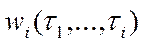 в виде разложения по заданной системе функций
в виде разложения по заданной системе функций 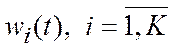
1)  , если
, если 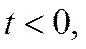
2) 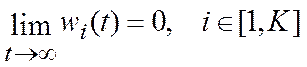
n =2
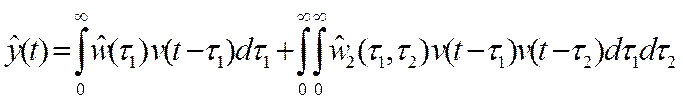 (13)
(13)
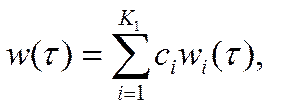 (13a)
(13a)
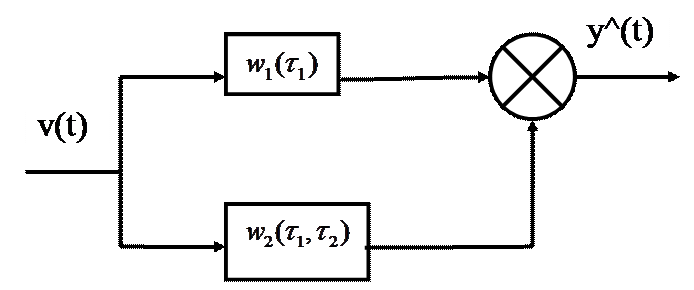
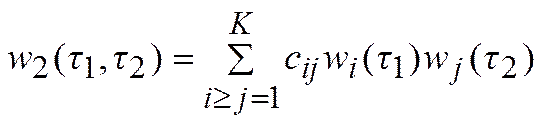 . (14)
. (14)

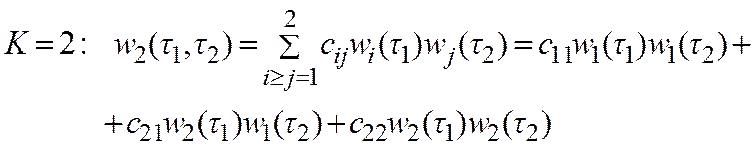
Подставляя выражения (13a), (14) в (13), получаем:
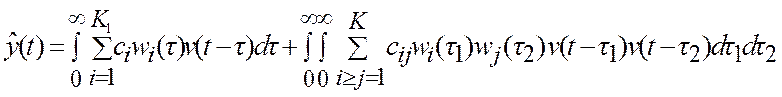
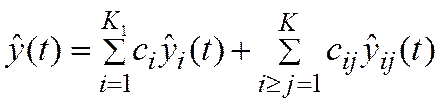 , (15)
, (15)
где
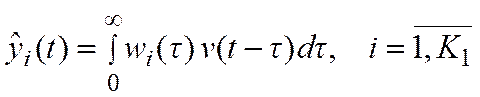
— реакция линейного элемента с весовой функцией 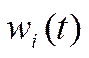 на входной сигнал v(t);
на входной сигнал v(t);
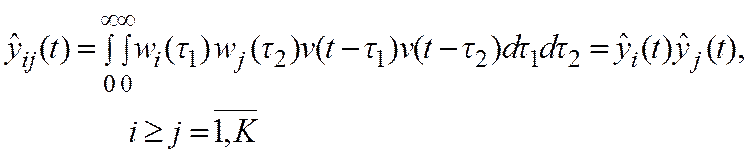
Теперь задача идентификации сведена к определению параметров разложения (15), т. е.
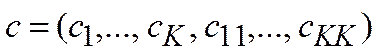 .
.
Общее число этих параметров 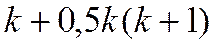
|
|
|
Модель Гаммерштейна
Рассмотрим модель Гаммерштейна с одним входом и одним выходом
|
|
|
 |
НЧ ЛЧ
Здесь ставится задачу идентификации двух функций  и
и 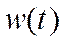
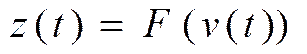
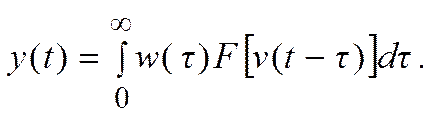 (16)
(16)
 (17)
(17)
 (18)
(18)
Подставим выражения (17), (18) в (16):
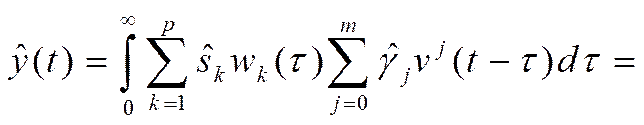
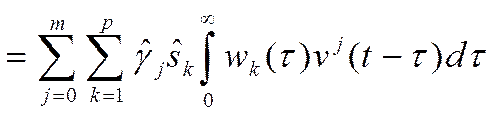
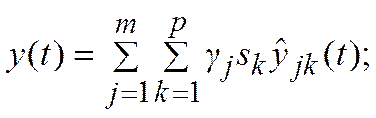 (19)
(19)
где

 .
.
:
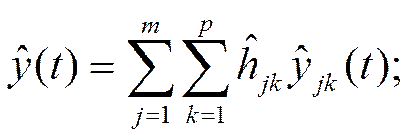 (20)
(20)
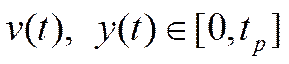
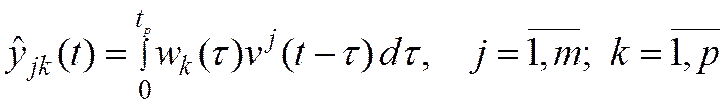
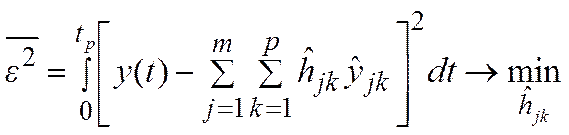
Модель Винера: ОУ - последовательное соединение динамического линейного звена с весовой функцией 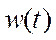 и нелинейного безынерционного
и нелинейного безынерционного  .
.
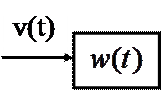 |  | ||

 (21)
(21)
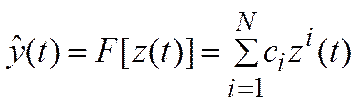 (22)
(22)
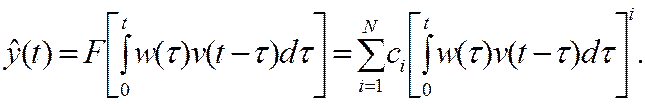 (23)
(23)
Запишем степень интеграла в виде произведения интегралов
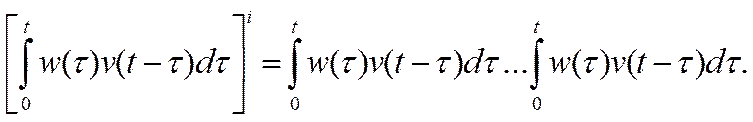
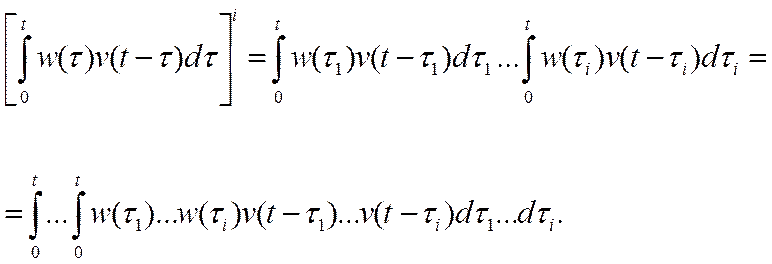
(24)
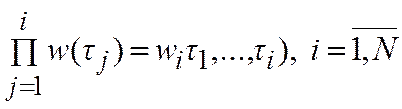 , - (25)
, - (25)
- сепарабельная функция
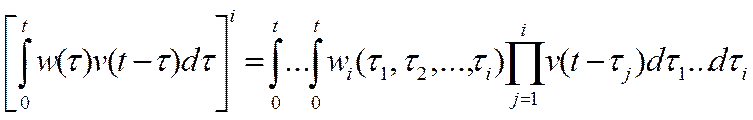
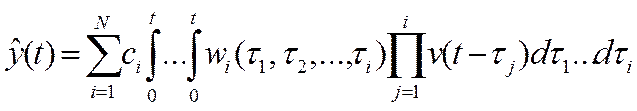 (26)
(26)
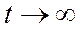
· Любую динамическую нелинейную систему без обратной связи, образованную соединением инерционных линейных систем и аналитических безынерционных нелинейностей, можно описать рядом Вольтерра.
Любую функциональную нелинейную систему без обратной связи, образованную соединением инерционных линейных систем и аналитических безынерционных нелинейностей, можно описать рядом Вольтерра.
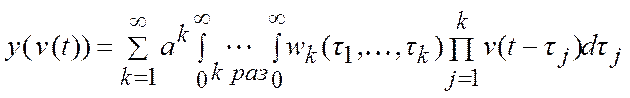
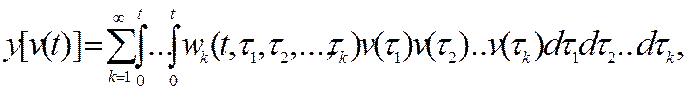
Если линейная часть системы - апериодическое звено с коэффициентом усиления К и постоянной времени Т, то
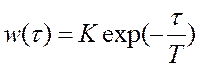 ,
, 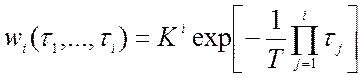 .
.
Приведенные примеры являются иллюстрацией к общему положению, согласно которому любую функциональную нелинейную систему без обратной связи, образованную соединением инерционных линейных систем и аналитических безынерционных нелинейностей, можно описать рядом Вольтерра..
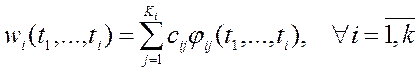 , (13)
, (13)
где 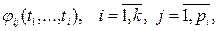 - выбранная система функций, содержащая
- выбранная система функций, содержащая 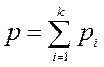 элементов.
элементов.
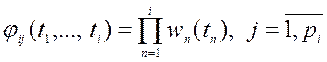 . (14)
. (14)
|
|
|




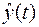 (t)
(t)