В результате выполнения домашней работы необходимо выполнить следующее:

СТАРООСКОЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

ИМ. А.А. УГАРОВА

(филиал) федерального государственного автономного образовательного

учреждения высшего профессионального образования

«Национальный исследовательский технологический университет «МИСиС»

 

 

Кафедра АИСУ

 

 

Основина О.Н.

 

Диагностика и надежность

автоматизированных систем

Методические указания

по выполнению домашних заданий

для студентов направлений:

220700 (15.03.040) – Автоматизация технологических процессов и производств;

140400 (13.03.02) – Электроэнергетика и электротехника;

(для всех форм обучения)

 

 

Одобрено редакционно-издательским советом института

 

 

Старый Оскол

УДК 621.38

ББК 32.85

Рецензент: Главный энергетик УЖДТ ОАО «ЛГОК», С.В. Зиновьев

 

Основина О.Н. Диагностика и надежность автоматизированных систем. Методические указания по выполнению домашних заданий. – Старый Оскол: СТИ НИТУ «МИСиС», 2014. – 52 с.

 

 

Методические указания по выполнению домашних
заданий по курсу «Диагностика и надежность автоматизированных систем», для студентов направлений:
220700 (15.03.040) – «Автоматизация технологических процессов и производств, 140400 (13.03.02) – «Электроэнергетика и электротехника»; для всех форм обучения.

 

© Основина О.Н.

© СТИ НИТУ «МИСиС»

СОДЕРЖАНИЕ

 

ПРЕДИСЛОВИЕ. 4

ЦЕЛИ И ЗАДАЧИ ДОМАШНИХ ЗАДАНИЙ.. 4

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ.. 5

ТЕМА 1. Количественная оценка показателей надежности невосстанавливаемых систем.. 5

1.1. Основные теоретические положения по теме 1. 5

1.2. Примеры решения задач по теме 1. 9

1.3. Контрольные вопросы и задания по теме 1. 10

ТЕМА 2. Методы расчета надежности невосстанавливаемых систем 11

2.1. Основные теоретические положения по теме 2. 11

2.1.1. Классический метод. 11

2.1.2. Метод перебора состояний. 13

2.1.3. Метод разложения относительно особого элемента. 15

2.1.4. Метод минимальных путей и сечений. 16

2.2. Примеры решения задач по теме 2. 17

2.3. Контрольные вопросы и задания по теме 2. 19

ТЕМА 3. Расчет надежности сложноструктурных систем логико-вероятностным методом.. 19

3.1. Основные теоретические положения по теме 3. 20

3.2. Методика расчета показателей надежности невосстанавливаемых систем 23

3.3. Преобразование структуры типа «треугольник» в структуру типа «звезда» 24

3.4. Алгоритм разрезания. 25

3.5. Примеры решения задач по теме 3. 26

3.6. Методика расчета показателей надежности восстанавливаемых систем 30

3.7. Примеры решения задач по теме 3. 32

3.8. Контрольные вопросы и задания по теме 3. 34

4. ПРАКТИЧЕСКОЕ ВЫПОЛНЕНИЕ ДОМАШНИХ ЗАДАНИЙ.. 34

4. 1. СОДЕРЖАНИЕ ДОМАШНЕГО ЗАДАНИЯ №1. 34

4.2. СОДЕРЖАНИЕ ДОМАШНЕГО ЗАДАНИЯ № 2. 40

5. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ДОМАШНИХ ЗАДАНИЙ.. 49

Список литературы.. 51

 

 

ПРЕДИСЛОВИЕ

Актуальность проблемы надежности современных автоматизированных систем (АС) очень велика и продолжает возра­стать во времени, требуя новых, системных подходов к ее решению. При создании многофункциональных автоматизированных систем на основе локальных вычис­лительных сетей, требуется оценка надежности всех без исключения разнородных компонентов: функций, техники, программ, персонала. Специфика этих компо­нентов велика, но, тем не менее, конкретные методы расчета их надежности основываются на общих концепци­ях и приемах, которые рассматриваются в дисциплине «Диагностика и надежность автоматизированных систем» и без овладения которыми бакалавр не сможет эффективно решать задачи проекти­рования и эксплуатации этих систем. В свою очередь успешное овладение методами анализа, расчета, обеспечения и повышения надежности современных автоматизированных систем прямо зависит от приоб­ретенных практических навыков. Специалисты в области теории надежности считают, что изучение этой теории без надлежащей практической подготовки бесцельно.

Для активизации работы студентов и контроля усвоения дисциплины рабочей программой курса предусмат­ривается выполнение домашних расчетно-графических заданий с выдачей ин­дивидуальных вариантов заданий. Контроль и самопроверка резуль­татов решения задач обеспечиваются получением числовых ответов.

 

ЦЕЛИ И ЗАДАЧИ ДОМАШНИХ ЗАДАНИЙ

Изучение курса «Диагностика и надежность автоматизированных систем» является частью подготовки бакалавров по направлениям «Автоматизация технологических процессов и производств», «Электроэнергетика и электротехника». В процессе изучения курса студенты выполняют два домашних задания, целью выполнения которых является: научиться производить, при необходимости, преобразование сетевой надежностно-функциональной схемы в эквивалентную ей по надёжности последовательно-параллельную с помощью следующих методов: классический, метод минимальных путей и сечений, метод разложения относительно особого элемента, логико-вероятностный метод.

Математическим аппаратом для решения перечисленных задач является: теория вероятности, математическая статистика, математическая логика. Поэтому перед началом изучения рассматриваемого курса важно восстановить в памяти основные понятия, определения, законы и формулы, относящиеся к этим разделам.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

 

ТЕМА 1. Количественная оценка показателей надежности невосстанавливаемых систем

 

В результате изучения темы 1 студенты должны знать и уметь:

· основные законы распределения дискретных и непрерывных случайных величин и базовые надежностные модели на их основе;

· группы показателей надежности (ПН), виды показателей, входящих в каждую группу и приемы их количественной оценки;

· выбирать сочетания ПН различных групп для всесторонней оценки надежности сложных систем;

· рассчитывать одни ПН через известные другие;

· оценивать надежность систем через ПН их элементов.

 

1.1. Основные теоретические положения по теме 1

Основные законы распределения наработки до отказа

Экспоненциальное распределение. Непрерывная случайная величина — наработка системы до отказа может описываться различными законами распределения взависимости от свойств системы и ее элементов, условий работы, характера отказов и др. Наибольшее распространение получило экспоненциальное (показательное) распределение, при котором функция распределения наработки до отказа:

F(t) = l- е , (1.1)

где — параметр этого распределения.

Плотность распределения:

, (1.2)

Функция надежности:

P(t)= e . (1.3)

Вероятность отказа системы до момента t ₁и вероятность безотказной работы до момента t ₁ соответственно будут:

; ;

Средняя наработка до отказа:

, (1.4)

т.е. равна величине, обратной параметру экспоненциального распределения.

Дисперсия наработки до отказа:

(1.5)

Интенсивность отказов:

(1.6)

является постоянной величиной, не зависящей от времени и численно равной параметру экспоненциального распределения.

Отметим одно характерное свойство, присущее только экспоненциальному распределению: вероятность Р (t₁, t ₂) безотказной работы системы на интервале (t₁, t₂) (при условии, что в момент t₁ система работоспособна) зависит только от длины интервала (t₂—t₁) и не зависит от времени t₁ предшествующей работы системы, т. е. от ее «возраста»:

(1.7)

Так как для экспоненциального закона характерно постоянство интенсивности отказов = const, то область применения этого закона — системы и элементы, где можно не учитывать ни период приработки, ни участок старения и износа (например, многие средства вычислительной техники и регулирования). Можно показать, что экспоненциальное распределение хорошо описывает время безотказной работы сложных систем, состоящих из большого числа разнородных компонентов. Наконец, одна из основных причин широкого использования экспоненциального закона заключается в том, что вследствие неизменности величины расчеты надежности при применении этого распределения наиболее просты.

Нормальное распределение. В отличие от экспоненциального нормальное распределение используют для описания таких систем и особенно их элементов, которые подвержены действию износа. Функция и плотность распределения наработки до отказа Т при этом соответственно будут:

, (1. 8)

 

, (1.9)

где и т — параметры нормального распределения.

Средняя наработка до отказа и дисперсия наработки до отказа:

=m; D[T]= ². (1. 10)

Для практического использования соотношений (1.8) и (1.9) перейдем от случайной величины Т к иной случайной величине

Z=(T—m)/ , (1.11)

имеющей математическое ожидание M[Z]=0 и дисперсию D[Z] = 1.

Согласно правилам определения закона распределения функции случайного аргумента плотность распределения величины Z

.

Соответственно функция распределения величины Z

.

Очевидно, что функция является симметричной, т. е. = , а, следовательно,

В таблицах часто приводят значения не функции Ф(z), анесколько иной функции

(1.12)

Функции Ф(z) и Ф₀ связаны между собой соотношением

(1.13)

Приведем значения функции (1.12) для нескольких положительных z:

Ф₀(0,5) =0,191; Ф₀(1) =0,343; Ф₀(2) =0,477.

Нормальное распределение описывает поведение случайных величин в диапазоне (— , ). Однако наработка до отказа является неотрицательной величиной, чтобы это учесть вместо нормального, в принципе, должно использоваться усеченное нормальное распределение. Область возможных значений случайной величины Т может быть различной; ниже примем, что эта область (0, ), и проведем усечение распределения в точке t = 0. Тогда функция распределения случайной величины Т имеет вид:

где с — нормирующий множитель; , т — параметры распределения.

При этом плотность распределения

.

Значение с выбирают из условия, что площадь под кривой плотности распределения равна единице. Использовав подстановку (1.11), можно показать, что

.

В усеченном нормальном распределении средняя наработка до отказа и дисперсия наработки до отказа

; ,

где .

Усеченное нормальное распределение обычно применяют, если m<3 . В противоположном случае использование более простого нормального (неусеченного) распределения дает достаточную точность.

Распределение Вейбулла — Гнеденко. Втеории надежности получило применение распределение Вейбулла — Гнеденко, описываемое функцией и плотностью распределения соответственно

; .

Это двухпараметрическое распределение, где параметр k определяет вид плотности распределения, параметр — его масштаб. Так, при k=1 распределение Вейбулла — Гнеденко совпадает с экспоненциальным, когда интенсивность отказов постоянна; при k > 1интенсивность отказов монотонно возрастает, при k < 1монотонно убывает. Распределение Вейбулла — Гнеденко может быть применено для описания наработки до отказа ряда электронных и механических технических средств, включая период приработки.

Соотношения для определения показателей надежности для трех рассмотренных выше распределений даны в табл. 1.1.

 

Табл. 1.1.

Распре-деление	Функция надёжности P(t)	Плотность распределения	Интенсивность отказов	Средняя наработка до отказа
Экспонен-циальное
Нормаль- ное			см. прим.
Вейбулла-Гнеденко

 

Примечание: ,

где 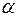, , , , - параметры соответствующих распределений; Г-гамма функция.

 

1.2. Примеры решения задач по теме 1

Пример 1. Функция вероятности безотказной работы (ВБР) системы описывается выражением .

Необходимо определить значение ВБР и среднюю наработку до отказа системы для оперативного времени t= 100 ч, еслиинтенсивности отказов ее элементов .

Неправильное решение задачи:

,

.

Правильное решение задачи:

ч.

.

Пример 2. Функция ВБР объекта имеет вид . Необходимо определить интенсивность отказов и среднюю наработку до отказа при значениях параметра а: , и , если оперативное время составляет .

Неправильное решение задачи:

а) так как задан закон распределения Вейбулла:

;

при ;

при ;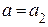

б) ;

; ;

; .

Из этого примера видно, что расхождение результатов расчета может быть недопустимо большим. В варианте «а» правильно рассчитан показатель и невер­но , а в варианте «б» - все наоборот.

Правильное решение задачи требует расчета значений показателя так, как это выполнено в варианте «а», показателя как в варианте «б».

 

1.3. Контрольные вопросы и задания по теме 1

1. Перечислите основные состояния, в которых может находиться система, элемент системы.

2. Что понимают под отказом, повреждением, восстановлением системы?

3. Дайте определение понятия «надежность АС» и его составляющих.

4. По каким признакам выделены группы ПН? Перечислите их.

5. Назовите основные показатели безотказности (ремонтопригодности, долговечности, комплексные ПН).

6. Запишите основные расчетные соотношения, связывающие между собой показатели безотказности в общем случае.

7. Назовите области применения основных законов распределения наработки до отказа.

8. Дайте вероятностные и статистические определения показателей надежности невосстанавливаемых систем.

9. В чем отличие коэффициентов готовности и оперативной готовности невосстанавливаемых систем?

 

ТЕМА 2. Методы расчета надежности
невосстанавливаемых систем

В результате изучения темы 2 студенты должны знать и уметь:

· области практического применения существующих методов оценки надежности невосстанавливаемых АС;

· принципы эквивалентного преобразования АС с простой структурой;

· принципы формирования минимальных путей и сечений;

· принципы выбора особых элементов в АС со сложной структурой;

· применять классический метод, метод перебора состояний, метод минимальных путей и сечений, метод разложения относительно особого элемента для получения количественных оценок показателей надежности невосстанавливаемых систем.

 

2.1. Основные теоретические положения по теме 2

При расчете вероятности безотказной работы, средней наработки до возникновения первого отказа элементы системы рассматриваются как невосстанавливаемые. В этом случае, если структура системы сводится к основному или резервному соединению элементов, при условии, что работа одного из параллельно соединенных элементов обеспечивает работоспособное состояние системы, показатели безотказности последней определяются по показателям безотказности элементов с использованием классического метода расчета надежности.

 

2.1.1. Классический метод

 

Поскольку при основном (последовательном) соединении элементов (см. рис. 2.1, а) работоспособное состояние системы имеет место при совпадении работоспособных состояний всех элементов, то вероятность этого состояния системы определяется произведением вероятностей работоспособных состояний всех элементов. Если система состоит из п последовательно включенных элементов, то при вероятности безотказной работы каждого из элементов р_i(t) вероятность безотказной работы системы

. (2.1)

При параллельном соединении элементов и при условии, что для работы системы достаточно работы одного из включенных параллельно элементов, отказ системы является совместным событием, имеющим место при отказе всех параллельно включенных элементов. Если параллельно включены т элементов (см. рис. 2.1, б) и вероятность отказа каждого q_j (t) = 1 —p_j (t), то вероятность отказа этой системы

. (2.2)

Если структурная схема надежности системы состоит из последовательно и параллельно соединенных элементов, то расчет ее надежности может быть произведен с использованием (2.1), (2.2).

а) б)

Рис. 2.1. Соединение элементов системы:
а – последовательное (основное); б – параллельное (резервное)

 

Чтобы определить значение средней наработки системы до отказа и другие показатели надежности, требуется знать законы распределения времени безотказной работы элементов (наработки до отказа) системы. Поскольку на участке нормальной эксплуатации с удовлетворительной точностью в качестве закона распределения времени безотказной работы элементов может быть принят экспоненциальный закон, то при основном соединении элементов, если выражение (2.1) примет следующий вид:

, (2.3)

где .

Таким образом, при основном соединении элементов, имеющих экспоненциальный закон распределения времени безотказной работы, закон распределения времени безотказной работы системы также будет экспоненциальным, в соответствии с этим имеем:

; ; ; . (2.4)

При резервном соединении т элементов, имеющих экспоненциальный закон распределения времени безотказной работы, вероятность отказа группы параллельно включенных элементов:

. (2.5)

Если все элементы равнонадежны и , то

; .

Таким образом, при резервном соединении элементов экспоненциальный закон распределения времени безотказной работы не сохраняется.

Во многих случаях рассмотренный выше способ расчета надежности не может быть использован, так как не всегда схема надежности содержит последовательно-параллельное соединение элементов.

Существуют несколько разновидностей классического метода расчета надежности систем со сложной структурой, часть из которых будет рассмотрена ниже применительно к анализу надежности мостиковой схемы, изображенной на рис. 2.2. (Эта схема не сводится к последовательно-параллельному соединению элементов.) Для всех элементов схемы известны вероятности безотказной работы р₁, р₂, р₃, р₄, p₅ и соответствующие им вероятности отказа типа «обрыв» q₁, q₂, q₃, q₄, q₅. Необходимо определить вероятность наличия цепи между точками а и b схемы.

 

Рис. 2.2. Мостиковая схема соединения элементов

 

2.1.2. Метод перебора состояний

Расчету надежности любой системы независимо от используемого метода предшествует определение двух непересекающихся множеств состояний элементов, соответствующих работоспособному и неработоспособному состояниям системы. Каждое из этих состояний характеризуется набором элементов, находящихся в работоспособном и неработоспособном состояниях. Поскольку при независимых отказах вероятность каждого из состояний определяется произведением вероятностей нахождения элементов в соответствующих состояниях, то при числе состояний, равном m, вероятность работоспособного состояния системы

. (2.6)

Тогда вероятность отказа

, (2.7)

где т — общее число работоспособных состояний, в каждом j - м из которых число исправных элементов равно l, а вышедших из строя — k.

Расчет с использованием метода перебора состояний удобно представить в виде табл. 2.1, где знаком «плюс» отмечены работоспособные состояния, а знаком «минус» — неработоспособные. В числовом примере все элементы приняты равнонадёжными с вероятностью безотказной работы, равной 0,9. Тогда за заданное время:

.

Из рассмотренного примера видно, что даже при сравнительно простой структуре применение метода перебора состояний сопряжено с громоздкими выкладками.

 

Табл 2.1.

Номер состояния	Состояние элементов	Вероятность состояний
	+	+	+	+	+	p1p2p3p4p5=0,95
	-	+	+	+	+	p2p3p4p5q1
	+	-	+	+	+	p1p3p4p5q2
	+	+	-	+	+	p1p2p4p4q3 0,1*0,94
	+	+	+	-	+	p1p2p3p5q4
	+	+	+	+	-	p1p2p3p4q5
	-	+	-	+	+	p2p4p5q1q3
	-	+	+	-	+	p2p3p5q1q4
	-	+	+	+	-	p2p3p4q1q5
	+	-	-	+	+	p1p4p5q2q3
	+	-	+	-	+	p1p3p5q2q4 0,12*0,93
	+	-	+	+	-	p1p3p4q2q5
	+	+	-	+	-	p1p2p4q3q5
	+	+	+	-	-	p1p2p3q4q5
	-	+	-	+	-	p2p4q1q3q5 0,13*0,92
	+	-	+	-	-	p1p3q2q4q5

 

2.1.3. Метод разложения относительно особого элемента

Этот метод основан на использовании формулы полной вероятности. В сложной системе выделяется особый элемент, все возможные состояния H_i которого образуют полную группу, . Если анализируемое состояние системы А, то его вероятность

, (2.8)

Второй сомножитель в (2.8) определяет вероятность состояния А при условии, что особый элемент находится в состоянии H_i. Рассмотрение H_i - го состояния особого элемента как безусловного позволяет упростить структурную схему надежности и свести ее к последовательно-параллельному соединению элементов.

Так, в рассматриваемой мостиковой схеме (рис. 2.2) выделение элемента 5 в качестве особого с двумя возможными состояниями (1 —работоспособное и 2 — неработоспособное, т.е. Р { Н ₁} =р₅; Р { Н ₂} =q₅) позволяет от структурной схемы, представленной на рис. 2.2, перейти при безусловно работоспособном состоянии элемента 5 к схеме, представленной на рис. 2.3, а. При отказе элемента 5 структурная схема имеет вид, представленный на рис. 2.3, б. Если состояние А — наличие цепи между а и b, то в соответствии с (2.1) и (2.2) имеем:

;

.

 

Рис. 2.3. Структурные схемы мостикового соединения элементов,
соответствующих работоспособному
(а) и неработоспособному (б) состояниям элемента 5

 

Сопоставление обоих методов расчета надежности показывает, что выделение особого элемента с последующим анализом упрощенных структурных схем существенно сокращает математические выкладки.

 

2.1.4. Метод минимальных путей и сечений

Вряде случаев для анализа надежности сложной системы бывает достаточным определить граничные оценки надежности сверху и снизу.

При оценке вероятности безотказной работы сверху P_Cmax определяют минимальные наборы работоспособных элементов (путей), обеспечивающих работоспособное состояние системы. При формировании пути, считая, что все элементы находятся в неработоспособном состоянии, последовательным переводом элементов вработоспособное состояние производят подбор вариантов соединений элементов, обеспечивающих наличие цепи.

Набор элементов образует минимальный путь, если исключение любого элемента из набора приводит к отказу пути. Из этого следует, что в пределах одного пути элементы находятся в основном соединении, а сами пути включаются параллельно. Так, для рассмотренной мостиковой схемы (рис. 2.2) набор минимальных путей представлен на рис. 2.4. Поскольку один и тот же элемент включается в два параллельных пути, то в результате расчета получается оценка безотказности сверху:

.

При определении минимальных сечений осуществляется подбор минимального числа элементов, перевод которых из работоспособного состояния в неработоспособное вызывает отказ системы. При правильном подборе элементов сечения возвращение любого из элементов в работоспособное состояние восстанавливает работоспособное состояние системы. Поскольку отказ каждого из сечений вызывает отказ системы, то первые соединяются последовательно. В пределах каждого сечения элементы соединяются параллельно, так как для работы системы достаточно наличия работоспособного состояния любого из элементов сечения.

Схема минимальных сечений для мостиковой схемы приведена на рис. 2.5. Поскольку один и тот же элемент включается в два сечения, то полученная оценка является оценкой снизу:

.

 

Рис. 2.4. Набор минимальных путей

 

Рис. 2.5. Набор минимальных сечений

 

В рассматриваемом примере оценка безотказности снизу совпадает с фактической безотказностью, рассчитанной по первым двум методам.

Таким образом, при составлении минимальных путей и сечений любая система преобразуется в структуру с параллельно-последовательным или последовательно-параллельным соединением элементов.

 

2.2. Примеры решения задач по теме 2

Пример 1. Определить вероятность безотказной работы системы, структурная надежностная схема которой представлена на рис. 2.6.

Рис. 2.6

 

Решение: Так как элементы рассматриваемой системы находятся в последовательно-параллельном соединении, то для расчета вероятности безотказной работы системы можно использовать классический метод:

.

Пример 2. Определить вероятность безотказной работы системы, структурная схема которой представлена на рис. 2.7. Для расчета использовать метод минимальных путей и сечений.

Рис. 2.7. Двойная мостиковая схема соединения элементов

 

Решение: Определим минимальные наборы работоспособных элементов (путей), обеспечивающих работоспособное состояние системы. Схема минимальных путей представлена на рис. 2.8, а. Так как полученная схема является последовательно – параллельной, для расчета вероятности безотказной работы системы можно использовать классический метод:

а) б)

Рис. 2.8. Набор минимальных путей
(а) и набор минимальных сечений (б)

 

Схема минимальных сечений представлена на рис. 2.8, б. Полученная схема также является последовательно – параллельной:

Пример 3. Определить вероятность безотказной работы двойной мостиковой схемы (см. рис. 2.7.) с использованием метода разложения относительно особого элемента.

Решение:

Используя формулу полной вероятности (2.8) и производя последовательное выделение двух особых элементов: пятого и шестого, получим вероятность безотказной работы двойной мостиковой схемы:

 

2.3. Контрольные вопросы и задания по теме 2

1. Какой элемент системы со сложной структурой рекомендуется выделять в качестве особого? Почему?

2. Почему методы минимальных путей и сечений дают оценки надежности соответственно сверху и снизу?

3. Как формируются минимальные пути (сечения)?

4. Структурные схемы какого вида принято называть основным (резервным) соединением элементов?

5. Назовите способы расчета показателей надежности системы через известные показатели надежности ее элементов при резервном соединении элементов.

6. В чем недостаток метода перебора состояний?

7. Когда можно использовать классический метод расчета надежности?

 

ТЕМА 3. Расчет надежности сложноструктурных систем
логико-вероятностным методом

В результате изучения темы 3 студенты должны знать и уметь:

· основные законы и тождества математической логики;

· методы и способы минимизации алгебраических выражений;

· способы представления функций работоспособности в алгебраической форме;

· способы получения функции работоспособности в бесповторной форме;

· принципы декомпозиции функции работоспособности, опирающиеся на теорему разложения математической логики;

· условия выполнения расчета показателей надежности для невосстанавливаемых и восстанавливаемых АС;

· алгоритм разрезания (разложения исходной структуры по ключевым элементам);

· преобразовывать структуры типа "треугольник" в эквивалентную ей по характерис­тикам надежности структуру типа "звезда";

· формировать звенья ненадежности системы;

· осуществлять переход от алгебраической формы запи

Поделиться:

Воспользуйтесь поиском по сайту: