 |
Численное дифференцирование
|
|
|
|
Численные методы решения систем линейных уравнений
Основные вопросы, рассматриваемые на лекции:
1. Метод простой итерации.
2. Метод Зейделя.
3. Метод исключения Гаусса.
- Метод простой итерации
Пусть дана система линейных уравнений  (1),
(1),
где 
Предполагая, что a ii  0 (i = 1,:,n) разрешим её относительно x 1, x 2,:, x n:
0 (i = 1,:,n) разрешим её относительно x 1, x 2,:, x n:
 (2),
(2),
где βi = b i / a ii, t ij = - a ij / a ii, при i  j, t ij = 0 при i = j.
j, t ij = 0 при i = j.
Систему (2) можно записать в виде  (2').
(2').
Теорема. Если матрица Т удовлетворяет одному из условий:
с  ,
,
то система уравнений (2) имеет единственное решение, которое может быть получено как предел последовательности, построенной по формулам 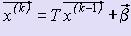 , k = 1, 2,:, начиная с произвольного x (0) = (x 1(0), x 2(0),:, x n(0)).
, k = 1, 2,:, начиная с произвольного x (0) = (x 1(0), x 2(0),:, x n(0)).
Процесс уточнения корня заканчивается, когда выполняется условие  , i = 1,:, n, где E - допустимая погрешность вычисления. При этом x (k) = (x 1(k), x 2(k),:, x n(k)) - решение системы (1).
, i = 1,:, n, где E - допустимая погрешность вычисления. При этом x (k) = (x 1(k), x 2(k),:, x n(k)) - решение системы (1).
· Метод Зейделя
Пусть дана система линейных уравнений (1). Сведём систему (1) к системе (2). Зададим некоторые начальные приближения неизвестных x 1(0) = β1, x 2(0) = β2,:, x n(0) = βn.
Подставим их в правые части системы и вычислим новые приближения, при этом будем использовать приближения к решениям, найденные при выполнении текущей итерации, т.е.
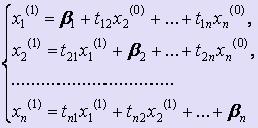
Аналогичным образом проводим вторую итерацию и т.д.
Процесс уточнения корня заканчивается, когда выполняется условие  , k = 1,:, n, где E - допустимая погрешность вычисления.
, k = 1,:, n, где E - допустимая погрешность вычисления.
Замечание: при решении системы линейных уравнений методом Зейделя итерационный процесс будет сходящимся лишь в случае, если для каждого уравнения выполняется условие  , i = 1,:, n, однако в сумму не входит слагаемое a ij c равными i и j. При этом хотя бы одно неравенство должно выполняться строго. Это условие является достаточным условием сходимости метода Зейделя.
, i = 1,:, n, однако в сумму не входит слагаемое a ij c равными i и j. При этом хотя бы одно неравенство должно выполняться строго. Это условие является достаточным условием сходимости метода Зейделя.
|
|
|
· Метод исключения Гаусса
(рассматривается решение систем уравнений данным методом и вычислений обратной матрицы с помощью метода Гаусса).
Метод исключения Гаусса относится к прямым методам решения систем линейных уравнений.
Идея этого метода заключается в том, чтобы исходную систему линейных уравнений  (1) с произвольной матрицей А свести некоторыми эквивалентными преобразованиями к системе вида
(1) с произвольной матрицей А свести некоторыми эквивалентными преобразованиями к системе вида  (2), где Ā - треугольная матрица.
(2), где Ā - треугольная матрица.
Затем из последнего уравнения системы (2) находится x n, из предыдущего - x n-1 и т.д.
Вычисление обратной матрицы с помощью метода Гаусса:
Пусть x i - i-ый столбец искомой обратной матрицы, e i - i-ый столбец единичной матрицы.
Т.к. A · A -1 = E, то 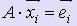 , при i = 1, 2,:, n. Задача нахождения обратной матрицы сводится к задаче решения n систем n линейных уравнений с одной и той же матрицей A, но с разными правыми частями.
, при i = 1, 2,:, n. Задача нахождения обратной матрицы сводится к задаче решения n систем n линейных уравнений с одной и той же матрицей A, но с разными правыми частями.
Интерполирование функций
Основные вопросы, рассматриваемые на лекции:
1. Основные понятия интерполяции, задача, приводящая к приближению функции, геометрический смысл интерполирования
2. Интерполяционный многочлен Лагранжа
3. Схема Эйткена
4. Оценка погрешности интерполяционной формулы Лагранжа
5. Конечные разности
6. Интерполяционные формулы Ньютона
§ Первая интерполяционная формула Ньютона
§ Вторая интерполяционная формула Ньютона
7. Оценка погрешностей первой и второй интерполяционных формул Ньютона
8. Обратное интерполирование
9. Интерполяция сплайнами
- Основные понятия интерполяции, задача, приводящая к приближению функции
Интерполяция (от лат. interpolation - изменение, переделка) - в математике и статистике, отыскание промежуточных значений величины по некоторым известным её значениям [Сов. энциклопедический словарь].
Задача, приводящая к приближению функции, заключается в следующем. Известны значения функции f (x) в точках x 1, x 2,:, x n; требуется восстановить её значения при других х.
Интерполяционный полином, передающий свойства функции f (x) будем строить в виде:
Pn(x) = c1φ1(x) + c2φ2(x) +: + cnφn(x), где φ1(x), φ2(x),:, φn(x) - класс линейно-независимых функций, при этом Pn(xi) = f (xi), i = 1, 2,:, n.
Таким образом, Pn(x)  f(x).
f(x).
Точки x1, x2,:, xn называются узлами интерполяции.
|
|
|
· Интерполяционный многочлен Лагранжа
Пусть известны значения функции f (x) в (n+1) точке x0, x1,:, xn. Тогда многочлен Лагранжа, передающий свойства функции f (x), можно записать так:

· Схема Эйткена
Схема Эйткена предлагает более удобную форму нахождения полинома Лагранжа.
Основная идея данного метода заключается в следующем.
На первом этапе вычисляются многочлены L0,1(x), L1,2(x),:, Ln-1,n(x), построенные на каждой паре соседних узлов 0,1; 1,2;:; n-1,n соответственно.
При этом  ,
, 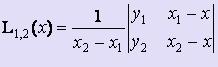 ,:,
,:,  .
.
Таким образом, многочлены, построенные на паре соседних узлов, вычисляются по формулам:  .
.
Затем на основе этих многочленов вычисляются многочлены, построенные на тройках соседних узлов:  .
.
И т.д. пока не получится один многочлен, построенный на всех узлах интерполяции:  .
.
Полученный многочлен L0, 1,..., n(x)  Ln(x).
Ln(x).
· Оценка погрешности интерполяционной формулы Лагранжа
Имеем yj = f (xj), Ln(x). Многочлен Ln(x) построен так, что Ln(xj) = f (xj).
Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа:  .
.
Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
· Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона
Пусть yi = f (xi), xi = x0 + ih, i = 1, 2,:, n.
Нужно построить Pn(x), удовлетворяющий двум условиям:
1. Степень полинома не должна превышать n.
2. Pn(xi) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: 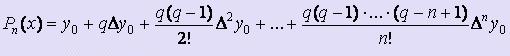 ,
,
где q = (x - x0) / h.
Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному x табличное значение.
- Вторая интерполяционная формула Ньютона
Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно.
Для этого применяется вторая интерполяционная формула Ньютона: ,
,
где q = (x - xn) / h.
Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
· Оценка погрешностей первой и второй интерполяционных формул Ньютона
|
|
|
Используя подстановки q = (x - x0) / h и q = (x - xn) / h и заменяя соответствующим образом выражение для П n+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно:
 ,
,
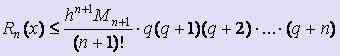 .
.
· Обратное интерполирование
Задача обратного интерполирования заключается в следующем. Если значения { yi } в таблице упорядочены по возрастанию или убыванию, то функция y = f (x) монотонна на [ x0, xn ], и эту же таблицу можно интерпретировать как задание дискретного образа функции x = φ(y), обратной по отношению к функции y = f(x). Для этой обратной функции также может быть поставлена задача интерполирования: найти значение x* по заданному значению y*.
Пусть { xi } равноотстоящие узлы, расположенные на расстоянии h друг от друга и построен один из полиномов Ньютона (для определённости - первый):  .
.
При решении задачи обратного интерполирования с помощью этого полинома в его левой части возникает известное значение y*, а сама формула становится алгебраическим уравнением относительно х. Если числа { yi } упорядочены по возрастанию или убыванию, то это уравнение имеет единственное решение на [ x0, xn ].
Его решение следует искать любым из изученных ранее методов для решения нелинейных уравнений.
В рассматриваемом нами случае наиболее естественным способом для решения уравнения является метод простой итерации.
Подставим y = y* в вышепредставленную формулу и преобразуем получившееся равенство к виду:  .
.
Это уравнение имеет структуру x = φ(x), т.е. по виду пригодно для применения метода простой итерации.
В качестве начального приближения можно взять значение x(0) = xi, ближайшее к искомому х*. Имея начальное приближение x(0), строим итерационный процесс для решения полученного уравнения пока не будет достигнута заданная точность: 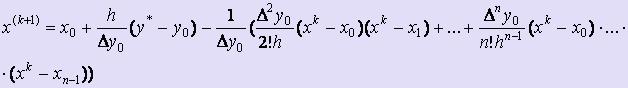
|
|
|
· Интерполяция сплайнами
При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений.
В этом случае удобно пользоваться особым видом кусочно-полиномиальной интерполяции - интерполяции сплайнами.
Суть этого подхода заключается в следующем.
Определение. Пусть отрезок [ a, b ] разбит точками на n частичных отрезков [ xi, xi+1 ], i = 0, 1,:, n-1. Сплайном порядка m называется функция Sm (x), обладающая следующими свойствами:
1) Функция Sm (x) непрерывна на отрезке [ a, b ] вместе со своими производными до некоторого порядка р.
2) На каждом отрезке [ xi, xi+1 ] функция совпадает с некоторым алгебраическим многочленом Pm,i (x) степени m.
Разность m - p между степенью сплайна и наивысшим порядком непрерывной на отрезке [ a, b ] производной называют дефектом сплайна.
Будем рассматривать сплайны, дефект которых равен 1.
Наиболее широкое распространение получили кубические сплайны S3 (x).
Итак, для осуществления интерполяции необходимо построить такой сплайн, что S(xi) = yi, i = 0, 1,:, n.
Согласно определению кубический сплайн можно представить в виде:  ,
,
где каждый из P 3, i (x) - многочлен третьей степени: 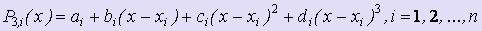 .
.
При этом коэффициенты ai = yi.
Можно показать, что коэффициенты сi вычисляются по формулам:  .
.
Для вычисления коэффициентов di используются формулы:  .
.
Для вычисления коэффициентов bi - формулы:  .
.
Численное дифференцирование
Основные вопросы, рассматриваемые на лекции:
1. Постановка задачи численного дифференцирования
2. Численное дифференцирование на основе интерполяционных формул Ньютона
3. Оценка погрешности дифференцирования с помощью многочлена Ньютона
4. Численное дифференцирование на основе интерполяционной формулы Лагранжа
5. Оценка погрешности численного дифференцирования с помощью многочлена Лагранжа
- Постановка задачи численного дифференцирования
Функция y = f(x) задана таблицей:
| x | x0 | x1 | ... | xn |
| y | y0 | y1 | ... | yn |
на отрезке [ a; b ] в узлах a = x0 < x1 < x2 <: <xn =b</x . Требуется найти приближенное значение производной этой функции в некоторой точке х*  [ a; b ]. При этом х* может быть как узловой точкой, так и расположенной между узлами.
[ a; b ]. При этом х* может быть как узловой точкой, так и расположенной между узлами.
· Численное дифференцирование на основе интерполяционных формул Ньютона
Считая узлы таблицы равноотстоящими, построим интерполяционный полином Ньютона. Затем продифференцируем его, полагая, что f '(x)  φ'(x) на [a; b]:
φ'(x) на [a; b]:
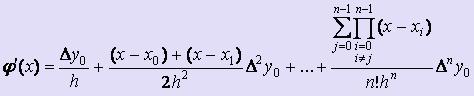 (1)
(1)
Формула значительно упрощается, если производная ищется в одном из узлов таблицы:х* = xi = x0 + ih:
 (2)
(2)
Подобным путём можно получить и производные функции f (x) более высоких порядков. Однако, каждый раз вычисляя значение производной функции f (x) в фиксированной точке х в качестве х0 следует брать ближайшее слева узловое значение аргумента.
|
|
|
· Численное дифференцирование на основе интерполяционной формулы Лагранжа
Запишем формулу Лагранжа для равноотстоящих узлов в более удобном виде для дифференцирования:

Затем, дифференцируя по х как функцию от t, получим:

Пользуясь этой формулой можно вычислять приближённые значения производной таблично-заданной функции f (x) в одном из равноотстоящих узлов.
Аналогично могут быть найдены значения производных функции f(x) более высоких порядков.
Численное интегрирование
Основные вопросы, рассматриваемые на лекции:
1. Постановка задачи численного интегрирования
2. Квадратурные формулы Ньютона-Котеса
3. Формулы прямоугольников
4. Формула трапеций
5. Формула Симпсона
6. Квадратурные формулы Гаусса
7. Метод Монте-Карло
1. Постановка задачи численного интегрирования
Требуется вычислить определённый интеграл вида  , причём функция может быть задана как в виде формулы, так и в виде таблицы.
, причём функция может быть задана как в виде формулы, так и в виде таблицы.
· Квадратурные формулы Ньютона-Котеса
 ,
,
где  - коэффициенты Котеса.
- коэффициенты Котеса.
Эти формулы дают на одном участке интегрирования различные представления для различного числа n отрезков разбиения.
· Формулы прямоугольников
Пусть требуется вычислить интеграл  .
.
Если отрезок интегрирования [a; b] достаточно велик, то нужно разбить его на более мелкие отрезки равной длины  , где n - число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла.
, где n - число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла.
Что касается построения прямоугольников, то их можно строить по-разному: можно проводить перпендикуляр до пересечения с кривой f (x) из правого конца каждого отрезка (Рис. 1), можно - из левого конца (Рис. 2)
 Рис. 1 Рис. 1
| 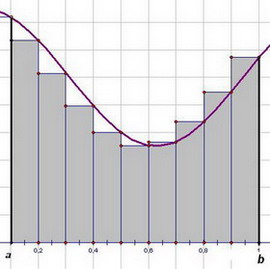 Рис. 2 Рис. 2
|
В зависимости от этого формулы для вычисления несколько различны и носят название формулы прямоугольников с правыми или левыми ординатами соотвественно:

(формула "правых" прямоугольников)

(формула "левых" прямоугольников)
Существует ещё формула "средних" прямоугольников:  , для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения:
, для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения:
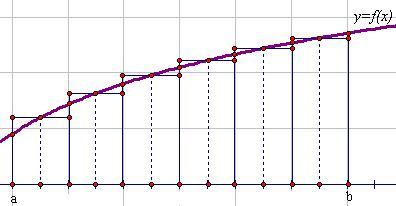
· Формула трапеций
Идея метода аналогична той, что представлена в методе прямоугольников. Отличие заключается в том, что на каждом отрезке разбиения криволинейная трапеция заменяется на обычную трапецию, площадь которой вычисляется по формуле  , где o1 и o2 - основания трапеции. Вычисляя и суммируя площади всех трапеций, получаем приближённое значение искомого интеграла: , где o1 и o2 - основания трапеции. Вычисляя и суммируя площади всех трапеций, получаем приближённое значение искомого интеграла:
| 
|

· Формула Симпсона
Заменяя на каждом отрезке разбиения часть кривой y = f (x) на параболическую кривую, вычисляя площади получившихся фигур и суммируя их, получим формулу Симпсона:
 ·
·
· Квадратурные формулы Гаусса
Традиционно при получении квадратурных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку [a; b] в интеграл по отрезку [-1; 1]:
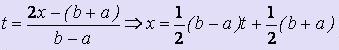 .
.
Тогда 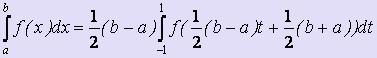 .
.
Будем использовать линейную интерполяцию подынтегральной функции.
Если вместо отрезка [-1; 1] взять в качестве узлов интерполяции подвижные узлы t1, t2, то нужно выбрать эти значения так, чтобы площадь трапеции, ограниченнной сверху прямой, проходящей через точки A1 (t1, φ(t1)) и A2 (t2, φ(t2)) была равной интегралу от любого многочлена некоторой наивысшей степени.
Полагая, что это многочлен третьей степени, вычислим t1, t2, которые получаются равными  и
и  , отличаясь лишь нумерацией значений.
, отличаясь лишь нумерацией значений.
Далее разбивая отрезок интегрирования на n частей, применяя к каждому из них описанную выше идею, можно получить формулу Гаусса: 
· Метод Монте-Карло
Идея метода:
Пусть f (x) > 0 (для простоты рассуждений). Возьмём число M, такое чтоf (x)  M для любого x из отрезка [a; b]. На графике - это прямая y = M. Используя счётчик случайных чисел можно получить точки, случайно и равномерно распределённые в прямоугольнике, образованном: M для любого x из отрезка [a; b]. На графике - это прямая y = M. Используя счётчик случайных чисел можно получить точки, случайно и равномерно распределённые в прямоугольнике, образованном:
| 
|
- отрезком [a; b] оси Ох
- отрезком, принадлежащим прямой y = M длины b-a
- отрезками, принадлежащими прямым х = a и x = b, заключёнными между осью Ох и прямой y = M.
Координаты таких точек вычисляются по формулам: 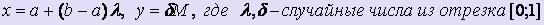 .
.
Если найдено таким образом n точек и k из них принадлежит криволинейной трапеции, ограниченной кривой y = f (x), прямыми x = a, x = b и осью Ох, то, с учётом того, что при больших n распределение точек по прямоугольнику близко к равномерному, то отношение k / nприближённо равно отношению площади криволинейноё трапеции к площади прямоугольника: 
При этом

Подставляя значения площадей и выражая интеграл, получаем: 
|
|
|


