 |
Раздел 1. Применение уравнения эмпирического закона изнашивания для аппроксимации экспериментальных данных зависимости коэффициента износа от совместной нагрузки.
|
|
|
|
Седакова Е.Б., Козырев Ю.П.
ПРОГНОЗИРОВАНИЕ ИЗНОСОТОЙКОСТИ ПОЛИМЕРНЫХ КОМПОЗИТОВ НА ОСНОВЕ ФИЗИЧЕСКОЙ МОДЕЛИ ИЗНАШИВАНИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО КУРСОВОМУ ПРОЕКТИРОВАНИЮ
САНКТ - ПЕТЕРБУРГ
2019
Раздел 1. Применение уравнения эмпирического закона изнашивания для аппроксимации экспериментальных данных зависимости коэффициента износа от совместной нагрузки.
Основной недостаток соотношений типа Арчарда и различных степенных уравнений состоит в том, что они описывают только монотонные зависимости износа от нагрузки. Однако ряд авторов, например, [1, 2] отмечает нелинейность параметров износа от величины нагрузки. Наличие критических точек на зависимости интенсивности линейного изнашивания от нагрузки (рис. 1), связанных с переходом от одного механизма изнашивания к другому, отмечается и в [3]
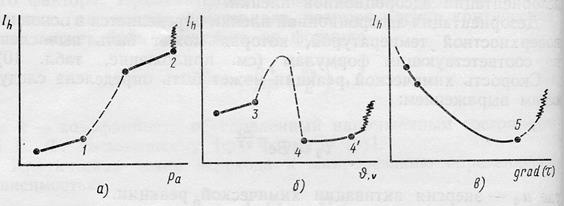
Рис. 1. Критические точки, характеризующие скачкообразное изменение износа. а). Критические точки, возникающие при росте давления. 1- точка, соответствующая переходу от упругих деформаций к пластическим; 2-точка, соответствующая переходу от пластических деформаций к микрорезанию.
б). Критические точки, возникающие при росте температуры или скорости скольжения. 3- точка, соответствующая разрушению адсорбционной пленки; 4- точка, соответствующая образованию пленки химического соединения; 4¢ - точка, соответствующая переходу к задиру при диссоциации пленки химического соединения. в). Критические точки, возникающие при росте температурного градиента. Рост температурного градиента ведет к снижению износа. 5- точка, соответствующая общему размягчению поверхностного слоя, приводящего к его намазыванию [3].
|
|
|
Наличие критических точек предполагает неприменимость монотонных зависимостей при описании последовательной смены механизмов износа. Эмпирический закон изнашивания (ЭЗИ) в виде
, (1)
где a, b, c, d - размерные коэффициенты
определяет величину коэффициента износа К, как функцию совместной нагрузки pv, где p - удельное давление, v - скорость скольжения.
Величина p v нашла широкое применение при определении допустимых и предельных нагрузок на узел трения. ЭЗИ описывает износ в диапазоне нагрузок от нуля до допустимых значений с учетом действующих механизмов изнашивания и их температурных зависимостей в рассматриваемом диапазоне нагрузок. Первое слагаемое в (1) имеет вид колоколообразной кривой, так как содержит экспоненту с отрицательным показателем степени. Второе слагаемое при достаточно малом показателе степени дает монотонно возрастающую функцию от pv. Таким образом, каждое слагаемое описывает принципиально различные механизмы износа. Коэффициенты в соотношении (1) являются размерными.
Результаты экспериментальных исследований материала Ф4К15М5 (·) и их аппроксимация по ЭЗИ представлены на рис. 2.
К, м3/Н м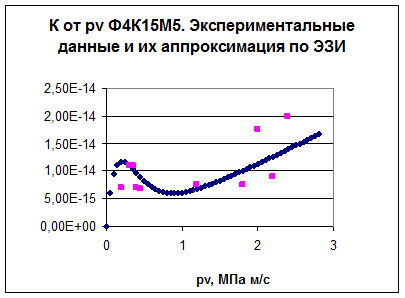 
pv, МПа м/с
Рис. 2. Зависимость величины коэффициента износа от совместной нагрузки для материалов: Ф4К15М5; ■ - экспериментальные точки Ф4К15М5; Коэффициенты в уравнении (1) для Ф4К15М5: a=1,5 10-13 м c (Н МПа)-1;
b=5,15 (МПа м/с)-1; c=4 10-14 (МПа)-1; d=0,125 (МПа м/с)-1.
Все коэффициенты, входящие в уравнение ЭЗИ, имеют размерности:
а = [м c (Н МПа)-1], b =[(МПа м/с)-1], c =[(МПа)-1], d =[(МПа м/с)-1].
В табл. 1 приведены значения размерных коэффициентов, входящих в уравнение ЭЗИ, для различных исследованных материалов, и диапазон исследованых pv. Коэффициент корреляции ЭЗИ с экспериментальными данными коэффициента износа материалов,приведенных в табл. 1, составляет 0,75 – 0,86.
Таблица 1. Величины размерных коэффициентов ЭЗИ для различных материалов
|
|
|
| № п/п | Материал | a, м с (Н МПа)-1 | b, (МПа м/с)-1 | c, (МПа)-1 | d, (МПа м/с)-1 | диапазоны pv МПа м\с |
| 1 | ПТФЭ | 2,4E-11 | 10,8 | 5E-13 | 0,85 | 0¸1,7 |
| 2 | ПА6 | 6,4E-13 | 7 | 4,9E-15 | 1,35 | 0¸2,5 |
| 3 | СВМПЭ | 4,6 E-13 | 6,4 | 6,7E-16 | 4,5 | 0¸1,7 |
| 5 | КВ (ПТФЭ + углерод) | 2,00E-13 | 5,4 | 7,00 E-15 | 0,3 | 0¸4,2 |
| 6 | МЛ С-3 (ПТФЭ + 70 вес. % углерода + 0,8 вес. % хрома + 2 вес.% Fe) | 1,50Е-14 | 1,1 | 4,00Е-15 | 0,17 | 0¸6 |
| 7 | Нигран | 1,90E-12 | 0,619 | 2,50E-12 | 0,0037 | 0¸9 |
| 8 | АГ-600 СО5 | 1,30E-13 | 0,65 | 5,40E-15 | 0,12 | 0¸17 |
| 9 | АГ-1500 СО5 | 3,8 0E-15 | 0,55 | 3,70E-16 | 0,1 | 0¸17 |
| 10 | ЭГО Б83 | 1,60E-14 | 0,4 | 1,50E-17 | 0,5 | 0¸12 |
| 11 | ППГ Б83 | 4,00E-14 | 0,5 | 5,00E-15 | 0,08 | 0¸17 |
| 12 | Э-1 | 1,50E-15 | 5,15 | 4,00E-14 | 0,525 | 0¸4 |
| 13 | Э-2 | 1,00E-10 | 5,3 | 1,00E-15 | 5 | 0¸1,7 |
Пример применения уравнения ЭЗИ в качестве аппроксимирующей зависимости экспериментальных данных коэффициента износа материала Ф4К15М5, представлен на рис. 2. Из рис. 2 следует, что в некоторой средней области значений pv наблюдается тенденция к стабилизации K от pv. При этом величина K не только не растет с ростом pv, но даже несколько снижается. Протяженность этой области по оси абцисс для Ф4К15М5 составляет 0,3 МПа м/с и в значительной степени определяется составом материала. Причиной стабилизации К от pv может быть устойчивость формирующихся вторичных структур к воздействию условий трения в указанном диапазоне нагрузок. Влияние температуры в уравнении ЭЗИ учтено температурными параметрами – показателями степени экспонент, входящих в два слагаемых.
На рис. 3 представлены зависимости, построенные по первому и второму слагаемым уравнения ЭЗИ.
К, м3/Н м
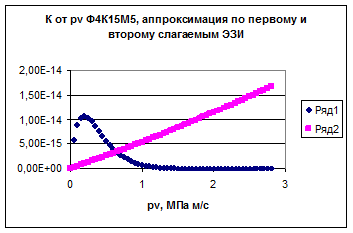pv, МПа м/с
Рис. 3. Зависимости K от pv, построенные по ЭЗИ: 1 – по первому слагаемому; 2 – по второму слагаемому.
К процессам изнашивания, описываемым первым слагаемым (1), относятся процессы, вызывающие образование и самоорганизацию вторичных структур. Вторичные структуры осуществляют защитные функции, ограничивая распространение взаимодействия внутри трущихся тел и препятствуя их непосредственному взаимодействию. При этом система трения стремится сосредоточить все виды взаимодействия в тонких поверхностных слоях.
Зависимость, построенная на рис. 3 по второму слагаемому соотношения (1), отражает монотонный рост К с увеличением аргумента. К группе процессов, описываемых вторым слагаемым (1), можно отнести механические процессы, например, отслаивание, пропахивание микронеровностями, усталостное разрушение. На эти процессы оказывает влияние снижение твердости материала, увеличение фактической площади контакта и снижение прочностных свойств. Учитывая вышесказанное, первую группу процессов можно назвать механохимическими, а вторую – механическими. Из рис. 3 следует, что во всем диапазоне изменения аргумента в величину износа материала вносят одновременно вклад и механические процессы, и механохимические процессы. Только в одном диапазоне изменения аргумента преобладают одни процессы, а в другом диапазоне – другие. На рис. 3 кривая 1, соответствующая механохимической составляющей изнашивания, и кривая 2, соответствующая механической составляющей изнашивания, имеют пересечение при р v =0,75 МПа м/с. Из рис. 3 следует, что при значениях pv >0, 75 МПа м/с наблюдается существенный рост механической составляющей изнашивания, что свидетельствует о преобладании в указанном диапазоне именно этой составляющей.
|
|
|
Из литературных источников [4, 5] следует, что значение [ pv ] для Ф4К15М5 находится в диапазоне 0,5 – 1,1 МПа м/с. По рис. 2 видно, что значение pv в минимуме кривой 1 соответствует 0,88 МПа м/с. Это значение pv попадает указанный диапазон и может быть принято за допускаемую величину pv для исследуемого композита.
В технических исследованиях часто используют величину интенсивности линейного изнашивания, которая показывает величину сближения поверхностей трения
I h = D h / L, (2)
где D h -толщина изношенного слоя.
Однако измерение малых толщин в реальных условиях эксперимента является сложной задачей. Поэтому в большинстве случаев после завершения экспериментов определяется массовый износ образца D m. Тогда
, (3)
где r -плотность материала.
В этом случае величина I h становится условной величиной, так как износ, происходящий в определенном месте номинального контакта, произвольно распределяется по всей площади контакта. Используя полученные в (1) размерные коэффициенты a, b, c, d и учитывая, что 
, перейдем к зависимости для интенсивности линейного изнашивания [6]
|
|
|
. (4)
Таким образом, по (4) для конкретной скорости скольжения можно построить зависимость I h от p, или для определенной величины контактного давления можно построить зависимости I h от v с учетом полученных ранее коэффициентов при построении зависимости, приведенной на рис. 2
В первом разделе курсового проекта студентам следует:
- используя ЭЗИ построить зависимости K от pv исследуемых материалов по предложенным вариантам;
- по зависимостям определить [ pv ] этих материалов;
- провести сравнительный анализ влияния величин коэффициентов a, b, c и d, входящих в уравнение ЭЗИ, на ширину диапазонов нагрузок, в которых преобладает определенная составляющая изнашивания, влияющая на общий износ материалов;
- отразить выводы по заданию в письменном виде.
Раздел 2. Прогнозирование износостойкости модельных композитов с импользованием ЭЗИ.
При создании новых композиционных материалов необходимо иметь сведения об износостойкости материалов на начальной стадии их разработки [7, 8]. Объединив параметры эмпирического закона изнашивания, полученные для составляющих композита, и, зная, распределение нагрузки между матрицей и наполнителем, выведем обобщенное выражение, содержащее как коэффициенты, относящиеся к матрице, так и коэффициенты, относящиеся к наполнителю. Вначале примем, что объемный износ полимерного композита при рассмотрении параллельной модели [9] определяется соотношением
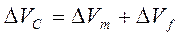(5)
где D Vm, D Vf – соответственно объемные износы матрицы и наполнителя.
Тогда выражение для Ih композита можно получить, применяя эмпирический закон изнашивания отдельно для матрицы и наполнителя, но с учетом распределения общей нагрузки по долям, приходящимся на матрицу и на структуру наполнителя, то есть, учитывая b и (1- b) соответственно [7, 8]. Обозначим размерные коэффициенты, относящиеся к матрице как a 1, b 1, c 1, d 1 , а коэффициенты, характеризующие наполнитель, как a 2, b 2, c 2, d 2. Тогда соотношение для Ih можно записать при учете (4) и (5) в виде
, (6)
где Ihm ; Ihf – интенсивности линейного изнашивания матрицы и наполнителя соответственно.
Однако, благодаря различным процессам взаимодействиям матрицы и наполнителя, Ih не является простой суммой интенсивностей линейного изнашивания матрицы и наполнителя. Это определяется существенным различием величин коэффициентов ЭЗИ, ответственных как за механизмы износа, так и за степень влияния температуры на физико-механические характеристики. Поэтому для характеристики износа композита разработаны условия выбора общих эквивалентных коэффициентов ЭЗИ [7, 8]. Отметим, что частицы наполнителя в композите всегда взаимодействуют с матрицей. При этом в отличие от свойств наполнителя физико-механические свойства полимерных матриц обычно в сильной степени зависят от температуры. В композите не могут одновременно протекать два диффузионных процесса, способствующих переносу материала для формирования вторичных структур. Представляется, что в реальном композите преобладает процесс, связанный с физико-механическими свойствами матрицы. На это указывают и то, что b1 >> b 2. Тогда примем b 1 в качестве коэффициента в показателе степени экспоненты в первом слагаемом ЭЗИ композита в целом. В то же время вклад других коэффициентов в общий эквивалентный коэффициент будет определяться нагруженностью матрицы b. Тогда физическая модель износа композита при учете выше сказанного принимает вид [7, 8]
|
|
|
. (7)
Обозначим в (7): a Э = 
; b Э = b 1; сЭ = b c 1 + (1- b)с2; d Э = b d 1 +(1- b) d 2. Тогда
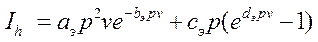. (8)
Для проверки справедливости (8) воспользуемся тем, что при отсутствии наполнителя (j f =0) нагруженность матрицы b =1. Подставляя эту величину в (8) получаем выражение для Ih полимерной матрицы.
Таким образом, для модельных композитов получаем физическую модель износа, математическим выражением которой является эмпирический закон изнашивания с эквивалентными коэффициентами в виде (8) [7, 8]. В результате появляется возможность сравнительной оценки триботехнических свойств разрабатываемых модельных композитов с промышленными композитами.
Нагруженность матрицы b в качестве параметра входит в выражения для определения эквивалентных коэффициентов. Параметры, входящие в расчетные соотношения для определения b зависят от структуры наполнителя, формируемой в композите.
Рассмотрим особенности определения b для пространственной структуры наполнителя в композите.
В случае использования наполнителя микронных размеров в полимерном композите формируется однослойная структура. При определении прочностных свойств такой структуры дисперсного наполнителя необходимо ввести прочностную характеристику структуры - сопротивление деформированию дисперсной среды E f. Величина концентрации частиц наполнителя на поверхности гранулы полимера j SK должна оказывать влияние на модуль упругости стенки из частиц наполнителя. Тогда для случая однослойного расположения дисперсных частиц наполнителя микронных размеров [11]
, (9)
где E f 0 – сопротивление деформированию дисперсной средыпри полном заполнении наполнителем слоя, примыкающего к поверхности частицы полимера, то есть при j SK =1, можно принять в качестве численного значения E f 0 модуль упругости тонких волокон материала наполнителя.
Исходя из суммарного числа частиц наполнителя на поверхности одной частицы полимера, имеющей площадь поверхности равную 6× rp 2, и, учитывая, что одна частица наполнителя в данной модели покрывает сразу две поверхности полимера, определим величину j SK в (9)
,
где rp – средний линейный размер частицы полимера; rf - средний линейный размер частицы наполнителя.
Если средние размеры наполнителя находятся в микронной области, то нагруженность матрицы определяется по соотношению
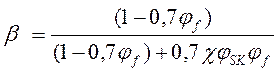, (11)
где j f - объемная концентрация наполнителя; c = E f 0 / Em, Em – модуль упругости матрицы.
В случае наполнения матрицы частицами наноразмеров в композите формируется многослойная пространственная структура вследствие высокой поверхностной активности наночастиц. Определим сопротивление деформирования Ef многослойной структуры наполнителя наноразмеров толщиной D w, состоящей из x fl слоев используем соотношение, которое включает коэффициент D E, зависящий от масштабного эффекта, и сомножитель, имеющий максимальное значение при определенной концентрации, зависящей от величины постоянной толщины стенки tc [10, 11]
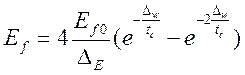, (12)
где D w - толщина стенки структуры наполнителя, 
, rp . – средний размер гранулы полимера; D E – коэффициент, зависящий от размера частиц наполнителя, 
, v 1 и v Э объем единичной частицы наполнителя и объем эталонной частицы наполнителя, соответственно; в качестве эталонной можно принять частицу наполнителя со средним линейным размером 10 нм, mh - модуль Вейбулла, для частиц наполнителя из нанодиапзона от 10 нм до 100 нм можно принять mh =5; t с - постоянная толщины стенки структуры наполнителя,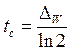 
.
Тогда с учетом (11 и 12) выражение для определения b в случае многослойной пространственной структуры нанонаполнителя, можно записать следующим образом [10, 11]
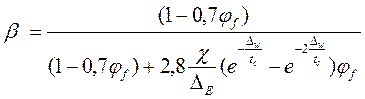. (13)
Часть выражения (12), представляющая собой разность экспонент, заключенная в скобки, является функцией с экстремумом. Для определения максимальной эффективной концентрации нанонаполнителя следует построить зависимость 
от j f. Тогда за максимальную эффективную концентрацию нанонаполнителя следует принять величина j f , соответствующую максимальному значению разности экспонент.
На рис. 4 в качестве примера приведены зависимости разности экспонент от j f для различных средних значений размеров частиц нанонаполнителя.
j f
Рис. 4. Зависимости разности экспонент в (12) от j f для различных средних значений размеров частиц нанонаполнителя: 1- rf =30 нм; 2- rf =50 нм; 3 - rf =100 нм.
Из рис. 4 следует, что наибольшая эффективная концентрация нанонаполнитля для rf =30 нм составляет 3%; для rf =50 нм составляет 12%; для rf =100 нм составляет 20%.
На рис. 5 приведены примеры зависимостей IhC от p, построенные для модельных композитов по (8) с нанонаполнителем при rf =50 и различных j f из диапазона 3 об.% до 12 об. %, определенного по зависимости рис. 4 с шагом в об. 3%.
IhC
p, МПа
Рис. 5. Зависимости IhC от p при различных j f , принятых диапазона до максимальной эффективной концентрации. v =0,3 м/с
Рассмотрим особенности определения b для случайной структуры наполнителя в композите.
Для случая формирования композита по технологии введения наполнителя в расплав полимерной матрицы с последующим соблюдением технологического процесса получаем случайную структуру наполнителя. Расчетное соотношение для определения b в этом случае имеет вид
, (14)
где Q – коэффициент усиления композита, Q=3/8; lm – средняя относительная длина агрегатов частиц наполнителя, 
; rf - средний размер частицы наполнителя; Ф – фактор фрактальности,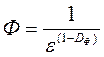 
; e - масштаб измерений периметра поперечного сечения единичного элемента дисперсного наполнителя, e = rf Э / rf; rf Э - эталон измерений, rf Э =10 нм; DФ - фрактальная размерность, DФ для большого числа объектов - площадей, ограниченных замкнутой линией находится в пределах 1,2-1,4 [12], тогда примем DФ =1,3.
В табл. 2 приведены значения lm в зависимости от объемной концентрации наполнителя, полученные в результате компьютерного моделирования наполнения матрицы дисперсными частицами.
Таблица.2 Результаты расчета средней относительной длины агрегатов в зависимости от величины объемной концентрации дисперсного наполнителя [13]
| Объемная концентрация наполнителя, j f , % | 0,3 | 0,5 | 1 | 5 | 10 | 20 | 30 | 40 | 50 | 70 |
| Средняя относит. длина, lm | 1 | 1,07 | 1,16 | 1,36 | 1,40 | 1,87 | 2,28 | 2,78 | 3,30 | 5,14 |
Из табл. 2 следует, что величина lm в пределах небольшой статистической ошибки не зависит от размера частицы наполнителя при определенной концентрации наполнителя. В то же время величина lm сильно зависит от объемного содержания наполнителя. Практически процесс направленной агрегации частиц не наблюдается только при концентрациях £ 5 об. %. В то же время для j f =70 об. % величина lm достигает величины 5,14. При таких значениях lm композит вблизи поверхности трения близок по своей структуре к полимерному композиту, наполненному короткими волокнами [14, 15].
Во многих работах по полимерным композитам подчеркивается особая роль тонкого сорбированного слоя полимера на поверхности частицы наполнителя [16]. Этот слой обеспечивает адгезию между полимером и наполнителем и, в свою очередь, подвергается воздействию поверхности наполнителя. Объем сорбированного слоя растет с увеличением концентрации и уменьшением размеров частиц наполнителя, поэтому существуют определенные условия, при которых вся полимерная матрица будет находиться в сорбированном состоянии. Тогда при превышении определенной концентрации возникнет дефицит свободного несорбированного полимера, что приведет к ухудшению условий для образования адгезионного контакта между наполнителем и матрицей. Объем сорбированного полимера V СП в единице объема композита можно найти следующим образом
, (15)
где h СП -толщина сорбированного слоя, образующегося между полимером и наполнителем.
Объем полимера в единице объема композита V П в отсутствии сорбирования
. (16)
Тогда долю немодифицированного полимера в композите при наличии сорбирования можно найти из соотношения
. (17)
Для определения объема сорбированного полимера по (15) необходимо знание величины h СП. Эта величина определяется дальнодействием поверхностных сил частиц наполнителя. В [14] отмечается, что последовательное нарастание декорирующего вещества, инертного материала – полимера или угля, на поверхности свежерасщепленных пластинок слюды происходит до толщины в 1000 ангстрем. Свыше этого влияние подложки не проявляется. Примем половину этой толщины, 50 нм, за величину h СП.
Расчетные данные величины d по соотношению (17) в случае введения дисперсного наполнителя в расплав полимера приведены в табл. 3.
Таблица 3. Расчет величины d для случаев введения частиц наполнителя микро- и наноразмеров.
| Концентрация j f, % | Размер наполнителя rf, м | Доля немодифицированного полимера в композите d |
| 50 | 5 10-6 | 0,94 |
| 50 | 1 10-6 | 0,7 |
| 25 | 100 10-9 | 0 |
| 6,2 | 20 10-9 | 0 |
Из данных табл. 3 видно, что при rf = 1 и 5 мкм даже при самых больших используемых концентрациях сорбированный полимер составляет только малую часть от исходного полимера. С другой стороны при наполнителях наноразмеров полимерная матрица может переходить в сорбированное состояние уже при концентрации наполнителя порядка 6 об. %. Поэтому при применении нанонаполнителей необходимо учитывать эффект сорбирования матрицы композита.
Во втором разделе курсового проекта студентам следует:
- построить расчетные зависимости b от j f для композиционного материала с микро- и нанонаполнителем в соответствии с заданным вариантом;
- определить наиболее эффективные концентрации;
-построить расчетные зависимости IhC от p для модельных композитов с микро и нанонаполнителем в соответствии с вариантами. В расчетах принять v =0,3 м/с. При построении зависимостей учесть особенности структур, формируемых в композите микро- и нанонаполнителями, включая имеющиеся ограничения по величине объемной концентрации наполнителя;
- отразить выводы по заданию в письменном виде
Раздел 3. Оценка эффективности наполнения полимерных матриц с использованием ЭЗИ. Построение зависимостей ICm от pv и j f.
Разработанная физическая модель износа в виде (8) применима для оценки триботехнической эффективности наполнения полимерной матрицы на стадии разработки новых композитов [8]. Для этого используем величину IС m = Ih С / Ihm. Значение I С m дает количественную оценку снижения интенсивности линейного изнашивания композита. Кроме того, величина I С m учитывает тот факт, что износы матриц различных композитов могут отличаться на порядки при одних и тех же типах наполнителей.
Для определения Ih С используем выражение (8), а для определения Ihm – выражение (4). Разложим экспоненты, заключенные в скобки в (8) и (4), в ряд Тейлора и ограничимся первыми двумя слагаемыми. В результате получим для (8)
,
для (4) (18)
Подставив выражения (18) в (8) и (4), и при учете, что bЭ = b1 окончательно находим [8]
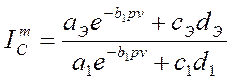. (19)
В третьем разделе курсового проекта студентам следует:
- построить зависимости по (179 ICm от pv и j f для модельных композитов в соответствии с заданными вариантами;
- в выводах по третьему разделу оценить эффективность наполнения полимерных матриц в соответствии с заданными вариантами на основании построенных зависимостей.
Отразить выводы по заданию в письменном виде.
Литература
1. Рыбин В.В., Бахарева В.Е., Анисимов А.В., Савелов А.С. Нано- и микромодификаторы антифрикционных углепластиков// Вопросы материаловедения. 2009. № 3. С. 229-241.
2. Rhee S.H. Ludema K.C. Transfer film a severe wear of polymers// In: The wear of non-metallic: Proc. Of the 3rd Leeds-Lyon symp. held in the Inst. Of tribology, Dep. Of mech. Engineering, the Univ. of Leeds, England, September, 1976. P. 11-17.
3. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. М.: Машиностроение, 1977. -528 с.
4. Кенько В. М. К вопросу стандартизации методов испытаний фрикционных пластмасс// Весцi АН БССР № 2. 1980. С. 52−57.
5. Справочник по триботехнике. Т. 1. Теоретические основы/ Под ред. М. Хебды, А.В. Чичинадзе. –М.: Машиностроение, 1989. -397 с.
6. Козырев Ю.П., Седакова Е.Б. Влияние состава углеродных композиционных материалов на их нагрузочную способность// Вестник машиностроения. 2008. N. 2. C. 28-31.
7. Козырев Ю.П., Седакова Е.Б. Приложение эмпирического закона изнашивания к вопросам прогнозирования износа композитов на основе политетрафторэтилена// Вопросы материаловедения. 2012. N. 4. С. 217-222.
8. Седакова Е.Б., Козырев Ю.П. Оценка эффективности наполнения полимерных композитов триботехнического назначения//Труды 3-ей Международной научно-практической конференции «Современное машиностроение. Наука и образование». Санкт-Петербург. 2013. С. 379-386.
9. Рабинович А.Л. Введение в механику формированных полимеров. М.: Наука, 1970. -481 с.
10. Особенности структуры композитов триботехнического назначения на основе политетрафторэтилена c наполнителями наноразмеров// Вопросы материаловедения. 2013. N. 2. С. 75-82.
11. Козырев Ю.П., Седакова Е.Б. Инженерная модель нанокомпозитов триботехнического применения на основе полимеров с многослойной структурой дисперсного наполнителя// Вестник машиностроения. 2011. N.1. C. 34-36.
12. Федер Е. Фракталы. М.: Мир, 1991. -260 с.
13. Козырев Ю.П., Седакова Е.Б. Влияние процесса направленной агрегации частиц на характеристики полимерных антифрикционных нанокомпозитов// Проблемы машиностроения и надежности машин. 2010. N.4. С. 86-91. (соавт. Козырев Ю.П.)
14. Берлин А.А., Вольфсон С.А., Ошмян В.Г., Ениколопов Н.С. Принципы создания композиционных полимерных материалов. М.: Химия. 1990. -240 с.
15. Friction and Wear of Polymer Composites/ Ed. by K. Fridrich – Amsterdam: Elsevier Scien. Pub., 1986. – 507 p.
16. Лущейкин Г.А. Моделирование и оптимизация полимерных материалов. М.: КолоС, 2009. -192 с.
|
|
|
